{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"source": [
"# numpy: arrays and functions\n",
"## 09/12/2023\n",
"\n",
"print view
\n",
"notebook"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Arrays\n",
"\n",
"`numpy` arrays are dense, continuous, uniformly sized blocks of identically typed data values"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"outputs": [],
"source": [
"import numpy as np\n",
"L = [[0,1],[2,3]]\n",
"A = np.array(L)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"L: [[0, 1], [2, 3]]\n",
"A:\n",
" [[0 1]\n",
" [2 3]]\n"
]
}
],
"source": [
"print(\"L:\",L)\n",
"print(\"A:\\n\",A)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" \n"
]
}
],
"source": [
"print(type(L),type(A))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"# Array Memory Layout"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"source": [
"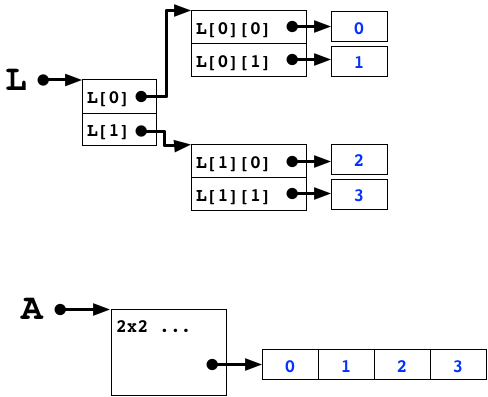 "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Array Memory"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In the standard python interpretter, the return value of `id` is the memory address of the object."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"4448783488\n"
]
}
],
"source": [
"print(id(L))"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"-128\n"
]
}
],
"source": [
"print(id(L[1])-id(L[0])) #rows are far away"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"32\n"
]
}
],
"source": [
"print(id(L[0][1])-id(L[0][0])) #columns not so much, but 32 bytes?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Why does this matter?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"Keeping data close together results in faster access times.\n",
" * It's easier to figure out the location of the data\n",
" * The data is more likely to fit in the processor's *cache*"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"## If you have a *block* of *dense* numerical data, store it in a `numpy` array"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"# Creating `numpy` Arrays"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note that `np.ndarray` and `np.array` are the same thing."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"dtype('int64')"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A = np.array([1,2,3,4])\n",
"A.dtype #type of what is stored in the array - NOT python types!"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"1"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A.ndim #number of dimensions (axes in numpy speak)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(4,)"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A.shape #size of the dimensions as a tuple"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(4, 1)"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A.reshape((4,1)).shape #a column vector"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"A = np.array([1,2,3,4]).reshape(4,1)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Initializing numpy Arrays"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"float64 (2, 3)\n"
]
}
],
"source": [
"#can initialize an array with a list, or list of lists (or list of lists of lists, etc)\n",
"M = np.array([[1,2,3],[4,5,6.0]])\n",
"print(M.dtype,M.shape)"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
"#if know the size, but not the data, can initialize to zeros:\n",
"Z = np.zeros((10,10))\n",
"#or ones\n",
"O = np.ones((5,10))\n",
"#or identity\n",
"I = np.identity(3) #this makes a 3x3 square identity matrix"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"float64\n"
]
}
],
"source": [
"print(Z.dtype) #note, default type is floating point"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"int64\n"
]
}
],
"source": [
"Z = np.zeros((10,10),np.int64) #can change\n",
"print(Z.dtype)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Indexing and Slicing"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"source": [
"`numpy` arrays can be indexed and sliced a lot like python lists, but take **tuples** of values to reference each dimension."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"outputs": [
{
"data": {
"text/plain": [
"array([[0, 1, 2],\n",
" [3, 4, 5]])"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"M = np.array([[0,1,2],[3,4,5]])\n",
"M"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"4\n",
"2\n"
]
}
],
"source": [
"print(M[1,1]) #indexing\n",
"print(M[0,-1]) #last item of first row"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[1 2]\n"
]
}
],
"source": [
"print(M[0,1:]) #can have slices - all but first column of first row"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[3 4 5] [3 4 5]\n"
]
}
],
"source": [
"print(M[1],M[1,:]) #missing indices are treated as complete slices"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"M = [[0,1,2],[3,4,5]]"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Advanced Slicing: Integer"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`numpy` arrays support advanced indexing by arrays of integers or booleans:"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [],
"source": [
"A = np.array([0,1,4,9,16,25])"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 4 25]\n"
]
}
],
"source": [
"print(A[[2,5]]) #choose just indices 2 and 5"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Advanced Slicing: Boolean\n",
"\n",
"Indexing by **Boolean** *numpy arrays* can be used to select elements"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[False False False True True True]\n"
]
}
],
"source": [
"b = A > 4\n",
"print(b)"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 9 16 25]\n"
]
}
],
"source": [
"print(A[b])"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Slicing Assignment"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"b = [False False False True True True]\n"
]
}
],
"source": [
"print(\"b =\",b)\n",
"A[b] = 0"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0 1 4 0 0 0]\n"
]
}
],
"source": [
"print(A)"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"S = np.array(['a','b','c','b','a'])\n",
"S[S != 'a'] = 'z'"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Array Views vs. Copies"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
" * A `numpy` array object has a pointer to a dense block of memory that stores the data of the array.\n",
" * *Basic* slices are just *views* of this data - they are **not** a new copy. \n",
" * Binding the same object to different variables will **not** create a copy.\n",
" * *Advanced* slices will create a copy if bound to a new variable - these are cases where the result may contain elements that are not contiguous in the original array "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Views"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [],
"source": [
"A = np.array([[0,1,2],[3,4,5],[6,7,8]])"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"True"
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"B = A #A and B reference the _same_ object\n",
"A is B"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[1000, 1, 2],\n",
" [ 3, 4, 5],\n",
" [ 6, 7, 8]])"
]
},
"execution_count": 36,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"B[0,0] = 1000\n",
"A"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Sliced Views"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([3, 4, 5])"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"row = A[1,:]\n",
"row"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[1000, 1, 2],\n",
" [ 3, 4, 5000],\n",
" [ 6, 7, 8]])"
]
},
"execution_count": 38,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"row[2] = 5000\n",
"A"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Explicit Copy"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[1000, 1, 2],\n",
" [ 3, 4, 5000],\n",
" [ 6, 7, 8]])"
]
},
"execution_count": 39,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"newMat = A.copy() #this will actually copy the data\n",
"newMat[0,0] = 0\n",
"A"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[ 0, 1, 2],\n",
" [ 3, 4, 5000],\n",
" [ 6, 7, 8]])"
]
},
"execution_count": 40,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"newMat"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Advanced Slices Copy"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([5, 6, 7, 8])"
]
},
"execution_count": 41,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A = np.array([[0,1,2],[3,4,5],[6,7,8]])\n",
"B = A[A > 4]\n",
"B"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([-1, -1, -1, -1])"
]
},
"execution_count": 42,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"B[:] = -1\n",
"B"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[0, 1, 2],\n",
" [3, 4, 5],\n",
" [6, 7, 8]])"
]
},
"execution_count": 43,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"but..."
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[ 0, 1, 2],\n",
" [ 3, 4, -1],\n",
" [-1, -1, -1]])"
]
},
"execution_count": 44,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A[A > 4] = -1\n",
"A"
]
},
{
"cell_type": "code",
"execution_count": 45,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"def z(M):\n",
" M[:] = 0\n",
"A = np.array([1,2,3])\n",
"z(A)"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Functions on Arrays\n",
"\n",
"`numpy` includes a number of standard functions that will work on arrays"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"2.5"
]
},
"execution_count": 47,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A = [1,2,3,4]\n",
"np.mean(A)"
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"10"
]
},
"execution_count": 48,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.sum(A)"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([ 0.84147098, 0.90929743, 0.14112001, -0.7568025 ])"
]
},
"execution_count": 49,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.sin(A)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Axis\n",
"\n",
"Most aggregation operations take an `axis` parameter that limits the operation to a specific direction in the array\n",
"* axis 0: across rows (apply operation to individual columns)\n",
"* axis 1: across columns (apply operation to individual rows)"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[ 0, 1, 2, 3],\n",
" [ 4, 5, 6, 7],\n",
" [ 8, 9, 10, 11]])"
]
},
"execution_count": 50,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b = np.arange(12).reshape(3,4); b"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"66"
]
},
"execution_count": 51,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.sum(b)"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([12, 15, 18, 21])"
]
},
"execution_count": 52,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.sum(b,axis=0)"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([ 6, 22, 38])"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.sum(b,axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Loading Data\n",
"\n",
"`genfromtxt` (and the simpler `loadtxt`) will read in deliminated files."
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([nan, nan, nan, ..., nan, nan, nan])"
]
},
"execution_count": 55,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.genfromtxt('../files/Spellman.csv')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The defaul delimiter is *whitespace* which will not work with a csv"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[ nan, 4.0000000e+01, 5.0000000e+01, ...,\n",
" 2.4000000e+02, 2.5000000e+02, 2.6000000e+02],\n",
" [ nan, -7.0000000e-02, -2.3000000e-01, ...,\n",
" 5.7000000e-01, 0.0000000e+00, 1.0000000e-02],\n",
" [ nan, 2.1500000e-01, 9.0000000e-02, ...,\n",
" -1.0000000e-01, 2.7000000e-01, 2.3500001e-01],\n",
" ...,\n",
" [ nan, -2.5500000e-01, -3.6000000e-01, ...,\n",
" 8.4000000e-01, -3.9000000e-01, -4.1500000e-01],\n",
" [ nan, 5.7000000e-01, 1.2000000e-01, ...,\n",
" -1.2000000e-01, 6.9000000e-01, 5.5500000e-01],\n",
" [ nan, 4.0500000e-01, 1.7000000e-01, ...,\n",
" -8.0000000e-02, 6.5000000e-01, 5.2000000e-01]])"
]
},
"execution_count": 56,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.genfromtxt('../files/Spellman.csv',delimiter=',')"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Why nan? "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Loading Data\n",
"\n",
"Recall that numpy arrays are dense, uniformly typed arrays. Can't mix a gene name (string) with expression values (float)."
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([['time', '40', '50', ..., '240', '250', '260'],\n",
" ['YAL001C', '-0.07', '-0.23', ..., '0.57', '0', '0.01'],\n",
" ['YAL014C', '0.215', '0.09', ..., '-0.1', '0.27', '0.23500001'],\n",
" ...,\n",
" ['YPR201W', '-0.255', '-0.36', ..., '0.84', '-0.39', '-0.415'],\n",
" ['YPR203W', '0.57', '0.12', ..., '-0.12', '0.69', '0.555'],\n",
" ['YPR204W', '0.405', '0.17', ..., '-0.08', '0.65', '0.52']],\n",
" dtype='\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 61,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Help on function genfromtxt in module numpy:\n",
"\n",
"genfromtxt(fname, dtype=, comments='#', delimiter=None, skip_header=0, skip_footer=0, converters=None, missing_values=None, filling_values=None, usecols=None, names=None, excludelist=None, deletechars=\" !#$%&'()*+,-./:;<=>?@[\\\\]^{|}~\", replace_space='_', autostrip=False, case_sensitive=True, defaultfmt='f%i', unpack=None, usemask=False, loose=True, invalid_raise=True, max_rows=None, encoding='bytes', *, ndmin=0, like=None)\n",
" Load data from a text file, with missing values handled as specified.\n",
" \n",
" Each line past the first `skip_header` lines is split at the `delimiter`\n",
" character, and characters following the `comments` character are discarded.\n",
" \n",
" Parameters\n",
" ----------\n",
" fname : file, str, pathlib.Path, list of str, generator\n",
" File, filename, list, or generator to read. If the filename\n",
" extension is ``.gz`` or ``.bz2``, the file is first decompressed. Note\n",
" that generators must return bytes or strings. The strings\n",
" in a list or produced by a generator are treated as lines.\n",
" dtype : dtype, optional\n",
" Data type of the resulting array.\n",
" If None, the dtypes will be determined by the contents of each\n",
" column, individually.\n",
" comments : str, optional\n",
" The character used to indicate the start of a comment.\n",
" All the characters occurring on a line after a comment are discarded.\n",
" delimiter : str, int, or sequence, optional\n",
" The string used to separate values. By default, any consecutive\n",
" whitespaces act as delimiter. An integer or sequence of integers\n",
" can also be provided as width(s) of each field.\n",
" skiprows : int, optional\n",
" `skiprows` was removed in numpy 1.10. Please use `skip_header` instead.\n",
" skip_header : int, optional\n",
" The number of lines to skip at the beginning of the file.\n",
" skip_footer : int, optional\n",
" The number of lines to skip at the end of the file.\n",
" converters : variable, optional\n",
" The set of functions that convert the data of a column to a value.\n",
" The converters can also be used to provide a default value\n",
" for missing data: ``converters = {3: lambda s: float(s or 0)}``.\n",
" missing : variable, optional\n",
" `missing` was removed in numpy 1.10. Please use `missing_values`\n",
" instead.\n",
" missing_values : variable, optional\n",
" The set of strings corresponding to missing data.\n",
" filling_values : variable, optional\n",
" The set of values to be used as default when the data are missing.\n",
" usecols : sequence, optional\n",
" Which columns to read, with 0 being the first. For example,\n",
" ``usecols = (1, 4, 5)`` will extract the 2nd, 5th and 6th columns.\n",
" names : {None, True, str, sequence}, optional\n",
" If `names` is True, the field names are read from the first line after\n",
" the first `skip_header` lines. This line can optionally be preceded\n",
" by a comment delimiter. If `names` is a sequence or a single-string of\n",
" comma-separated names, the names will be used to define the field names\n",
" in a structured dtype. If `names` is None, the names of the dtype\n",
" fields will be used, if any.\n",
" excludelist : sequence, optional\n",
" A list of names to exclude. This list is appended to the default list\n",
" ['return','file','print']. Excluded names are appended with an\n",
" underscore: for example, `file` would become `file_`.\n",
" deletechars : str, optional\n",
" A string combining invalid characters that must be deleted from the\n",
" names.\n",
" defaultfmt : str, optional\n",
" A format used to define default field names, such as \"f%i\" or \"f_%02i\".\n",
" autostrip : bool, optional\n",
" Whether to automatically strip white spaces from the variables.\n",
" replace_space : char, optional\n",
" Character(s) used in replacement of white spaces in the variable\n",
" names. By default, use a '_'.\n",
" case_sensitive : {True, False, 'upper', 'lower'}, optional\n",
" If True, field names are case sensitive.\n",
" If False or 'upper', field names are converted to upper case.\n",
" If 'lower', field names are converted to lower case.\n",
" unpack : bool, optional\n",
" If True, the returned array is transposed, so that arguments may be\n",
" unpacked using ``x, y, z = genfromtxt(...)``. When used with a\n",
" structured data-type, arrays are returned for each field.\n",
" Default is False.\n",
" usemask : bool, optional\n",
" If True, return a masked array.\n",
" If False, return a regular array.\n",
" loose : bool, optional\n",
" If True, do not raise errors for invalid values.\n",
" invalid_raise : bool, optional\n",
" If True, an exception is raised if an inconsistency is detected in the\n",
" number of columns.\n",
" If False, a warning is emitted and the offending lines are skipped.\n",
" max_rows : int, optional\n",
" The maximum number of rows to read. Must not be used with skip_footer\n",
" at the same time. If given, the value must be at least 1. Default is\n",
" to read the entire file.\n",
" \n",
" .. versionadded:: 1.10.0\n",
" encoding : str, optional\n",
" Encoding used to decode the inputfile. Does not apply when `fname` is\n",
" a file object. The special value 'bytes' enables backward compatibility\n",
" workarounds that ensure that you receive byte arrays when possible\n",
" and passes latin1 encoded strings to converters. Override this value to\n",
" receive unicode arrays and pass strings as input to converters. If set\n",
" to None the system default is used. The default value is 'bytes'.\n",
" \n",
" .. versionadded:: 1.14.0\n",
" ndmin : int, optional\n",
" Same parameter as `loadtxt`\n",
" \n",
" .. versionadded:: 1.23.0\n",
" like : array_like, optional\n",
" Reference object to allow the creation of arrays which are not\n",
" NumPy arrays. If an array-like passed in as ``like`` supports\n",
" the ``__array_function__`` protocol, the result will be defined\n",
" by it. In this case, it ensures the creation of an array object\n",
" compatible with that passed in via this argument.\n",
" \n",
" .. versionadded:: 1.20.0\n",
" \n",
" Returns\n",
" -------\n",
" out : ndarray\n",
" Data read from the text file. If `usemask` is True, this is a\n",
" masked array.\n",
" \n",
" See Also\n",
" --------\n",
" numpy.loadtxt : equivalent function when no data is missing.\n",
" \n",
" Notes\n",
" -----\n",
" * When spaces are used as delimiters, or when no delimiter has been given\n",
" as input, there should not be any missing data between two fields.\n",
" * When the variables are named (either by a flexible dtype or with `names`),\n",
" there must not be any header in the file (else a ValueError\n",
" exception is raised).\n",
" * Individual values are not stripped of spaces by default.\n",
" When using a custom converter, make sure the function does remove spaces.\n",
" \n",
" References\n",
" ----------\n",
" .. [1] NumPy User Guide, section `I/O with NumPy\n",
" `_.\n",
" \n",
" Examples\n",
" --------\n",
" >>> from io import StringIO\n",
" >>> import numpy as np\n",
" \n",
" Comma delimited file with mixed dtype\n",
" \n",
" >>> s = StringIO(u\"1,1.3,abcde\")\n",
" >>> data = np.genfromtxt(s, dtype=[('myint','i8'),('myfloat','f8'),\n",
" ... ('mystring','S5')], delimiter=\",\")\n",
" >>> data\n",
" array((1, 1.3, b'abcde'),\n",
" dtype=[('myint', '>> _ = s.seek(0) # needed for StringIO example only\n",
" >>> data = np.genfromtxt(s, dtype=None,\n",
" ... names = ['myint','myfloat','mystring'], delimiter=\",\")\n",
" >>> data\n",
" array((1, 1.3, b'abcde'),\n",
" dtype=[('myint', '>> _ = s.seek(0)\n",
" >>> data = np.genfromtxt(s, dtype=\"i8,f8,S5\",\n",
" ... names=['myint','myfloat','mystring'], delimiter=\",\")\n",
" >>> data\n",
" array((1, 1.3, b'abcde'),\n",
" dtype=[('myint', '>> s = StringIO(u\"11.3abcde\")\n",
" >>> data = np.genfromtxt(s, dtype=None, names=['intvar','fltvar','strvar'],\n",
" ... delimiter=[1,3,5])\n",
" >>> data\n",
" array((1, 1.3, b'abcde'),\n",
" dtype=[('intvar', '>> f = StringIO('''\n",
" ... text,# of chars\n",
" ... hello world,11\n",
" ... numpy,5''')\n",
" >>> np.genfromtxt(f, dtype='S12,S12', delimiter=',')\n",
" array([(b'text', b''), (b'hello world', b'11'), (b'numpy', b'5')],\n",
" dtype=[('f0', 'S12'), ('f1', 'S12')])\n",
"\n"
]
}
],
"source": [
"help(np.genfromtxt)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Data Normalization\n",
"\n",
"## Q1: How would you rescale your data to range from 0 to 1?\n",
"\n",
"## Q2: How would you rescale your data to have zero mean and unit standard deviation?"
]
},
{
"cell_type": "code",
"execution_count": 62,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"array([[0.51995439, 0.50171038, 0.51653364, ..., 0.59293044, 0.52793615,\n",
" 0.5290764 ],\n",
" [0.55245154, 0.5381984 , 0.53078677, ..., 0.51653364, 0.55872292,\n",
" 0.55473204],\n",
" [0.54503991, 0.54503991, 0.55302166, ..., 0.48916762, 0.55644242,\n",
" 0.54960091],\n",
" ...,\n",
" [0.49885975, 0.48688712, 0.49372862, ..., 0.62371722, 0.48346636,\n",
" 0.48061574],\n",
" [0.59293044, 0.54161916, 0.51995439, ..., 0.51425314, 0.60661345,\n",
" 0.59122007],\n",
" [0.57411631, 0.54732041, 0.52280502, ..., 0.51881414, 0.60205245,\n",
" 0.58722919]])"
]
},
"execution_count": 62,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"(values-values.min())/(values.max()-values.min())"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"0.9999999999999999"
]
},
"execution_count": 63,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.std((values-values.mean())/values.std())"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Project: Expression Data\n",
"\n",
"https://MSCBIO2025.github.io/files/Spellman.csv\n",
"\n",
"* Read this data into a numpy array\n",
"* Plot a histogram of the expression values for the first time point\n",
"* Plot a histogram of the expression values for the last time point\n",
"* Plot a histogram of the average expression value for the genes across all time points\n",
"* Plot the average expression value (across all genes) at each time point as a line graph\n",
"* Plot two series of average expression values: one for all genes where the first value is positive and the other for all genes where the first value is negative\n"
]
},
{
"cell_type": "code",
"execution_count": 64,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD4CAYAAAAXUaZHAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAAAOWUlEQVR4nO3df6jd9X3H8edrzvlHLajkLktjXKRkg3R0sVys0P5hcZu/xqKjE/1DXedICxEUhBEVZmEIga5269iEdIoWnFZQMaxh0wbB9Q+tUcQfia6hjZgQTVo3FYSO6Ht/3K96TO/NPeeec+6593OfDzjc7/fz/XHe3+Tklc/9fH+cVBWSpLb8xqQLkCSNnuEuSQ0y3CWpQYa7JDXIcJekBv3mpAsAWLVqVa1fv37SZUjSsvLss8/+oqqmZlu2JMJ9/fr17NmzZ9JlSNKykuS1uZY5LCNJDTLcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ1aEneoSurf+m0//Gj6wPZLJ1iJljJ77pLUIMNdkhpkuEtSgxxzlxrkuLzsuUtSgwx3SWqQwzJSI3qHYiR77pLUIMNdkhpkuEtSgxxzl5Yxx9k1l3l77knWJXkiyd4kLye5oWv/ZpJDSZ7vXpf0bHNzkv1JXk1y4TgPQNKJrd/2w49eWjn66bkfA26qqueSfBp4Nsnj3bLvVNXf966cZCNwJfA54DPAj5L8XlW9P8rCJUlzm7fnXlWHq+q5bvpdYB+w9gSbbAYeqKpfVdXPgf3AuaMoVpLUn4FOqCZZD5wDPN01XZ/khSR3Jzm9a1sLvN6z2UFm+c8gyZYke5LsOXr06OCVS5Lm1He4JzkVeAi4sareAe4EPgtsAg4D3x7kjatqR1VNV9X01NTUIJtKkubRV7gnOZmZYL+vqh4GqKo3q+r9qvoA+B4fD70cAtb1bH5m1yZJWiT9XC0T4C5gX1Xd0dO+pme1y4GXuumdwJVJTklyNrAB+MnoSpYkzaefq2W+BFwNvJjk+a7tFuCqJJuAAg4AXweoqpeTPAjsZeZKm61eKSNJi2vecK+qHwOZZdGuE2xzO3D7EHVJkobg4wckqUGGuyQ1yHCXpAYZ7pLUIMNdkhpkuEtSg3yeu7RE9T6i98D2SydYiZYje+6S1CDDXZIa5LCMtAz4LUoalD13SWqQ4S5JDTLcJalBjrlLK5SXWrbNnrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkNmjfck6xL8kSSvUleTnJD135GkseT/LT7eXrXniTfTbI/yQtJvjDug5AkfVI/PfdjwE1VtRE4D9iaZCOwDdhdVRuA3d08wMXAhu61Bbhz5FVLkk5o3nCvqsNV9Vw3/S6wD1gLbAbu7Va7F7ism94MfL9mPAWclmTNqAuXJM1toK/ZS7IeOAd4GlhdVYe7RW8Aq7vptcDrPZsd7NoO97SRZAszPXvOOuusQeuWtAC9X62ntvV9QjXJqcBDwI1V9U7vsqoqoAZ546raUVXTVTU9NTU1yKaSpHn0Fe5JTmYm2O+rqoe75jc/HG7pfh7p2g8B63o2P7NrkyQtkn6ulglwF7Cvqu7oWbQTuLabvhZ4tKf9mu6qmfOAt3uGbyRJi6CfMfcvAVcDLyZ5vmu7BdgOPJjkOuA14Ipu2S7gEmA/8B7wtVEWLEma37zhXlU/BjLH4gtmWb+ArUPWJUkagneoSlKDDHdJapDhLkkNMtwlqUGGuyQ1yHCXpAYZ7pLUoIEeHCZpvHywl0bFnrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkNMtwlqUGGuyQ1yG9ikvSJb4A6sP3SCVaiUbHnLkkNMtwlqUGGuyQ1yHCXpAbNG+5J7k5yJMlLPW3fTHIoyfPd65KeZTcn2Z/k1SQXjqtwSdLc+um53wNcNEv7d6pqU/faBZBkI3Al8Llum39JctKoipUk9WfecK+qJ4G3+tzfZuCBqvpVVf0c2A+cO0R9kqQFGGbM/fokL3TDNqd3bWuB13vWOdi1/ZokW5LsSbLn6NGjQ5QhSTreQsP9TuCzwCbgMPDtQXdQVTuqarqqpqemphZYhiRpNgsK96p6s6rer6oPgO/x8dDLIWBdz6pndm2SpEW0oHBPsqZn9nLgwytpdgJXJjklydnABuAnw5UoSRrUvM+WSXI/cD6wKslB4Dbg/CSbgAIOAF8HqKqXkzwI7AWOAVur6v2xVC5JmtO84V5VV83SfNcJ1r8duH2YoiRJw/EOVUlqkI/8lSbAR+xq3Oy5S1KD7LlL+oTe3yrA3yyWK3vuktQge+7ShB3fU5ZGwZ67JDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkNMtwlqUHexCTphHzI2fJkz12SGmS4S1KDHJaRFonPkNFisucuSQ0y3CWpQYa7JDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkNMtwlqUGGuyQ1aN5wT3J3kiNJXuppOyPJ40l+2v08vWtPku8m2Z/khSRfGGfxkqTZ9dNzvwe46Li2bcDuqtoA7O7mAS4GNnSvLcCdoylTkjSIecO9qp4E3jqueTNwbzd9L3BZT/v3a8ZTwGlJ1oyoVklSnxY65r66qg53028Aq7vptcDrPesd7Np+TZItSfYk2XP06NEFliFJms3QJ1SrqoBawHY7qmq6qqanpqaGLUOS1GOhX9bxZpI1VXW4G3Y50rUfAtb1rHdm1yatSH5BhyZloT33ncC13fS1wKM97dd0V82cB7zdM3wjSVok8/bck9wPnA+sSnIQuA3YDjyY5DrgNeCKbvVdwCXAfuA94GtjqFmSNI95w72qrppj0QWzrFvA1mGLkiQNxztUJalBhrskNchwl6QGGe6S1KCFXucuaQ5e266lwJ67JDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkN8jp3SQvSez3/ge2XTrASzcZwl9Q3b9BaPhyWkaQGGe6S1CDDXZIa5Ji7NAKORWupsecuSQ0y3CWpQYa7JDXIcJekBhnuktQgw12SGuSlkNICefmjljJ77pLUIHvukobmEyKXHnvuktQge+6SRspe/NIwVLgnOQC8C7wPHKuq6SRnAD8A1gMHgCuq6n+GK1OSNIhRDMt8pao2VdV0N78N2F1VG4Dd3bwkaRGNY8x9M3BvN30vcNkY3kOSdALDhnsBjyV5NsmWrm11VR3upt8AVs+2YZItSfYk2XP06NEhy5Ak9Rr2hOqXq+pQkt8GHk/ySu/CqqokNduGVbUD2AEwPT096zrSUuONS1ouhuq5V9Wh7ucR4BHgXODNJGsAup9Hhi1SkjSYBYd7kk8l+fSH08CfAC8BO4Fru9WuBR4dtkhJ0mCGGZZZDTyS5MP9/FtV/UeSZ4AHk1wHvAZcMXyZ0uQ4FKPlaMHhXlU/A/5wlvZfAhcMU5QkaTg+fkCSGmS4S1KDfLaMNAvH2bXcGe6SxsaHiE2OwzKS1CDDXZIa5LCMpEXhEM3isucuSQ0y3CWpQYa7JDXIcJekBnlCVSuWNyqpZYa7VhQDXSuFwzKS1CB77pIW3VzXvHst/OjYc5ekBtlzlzRRngcZD3vuktQge+6SljzH4gdnz12SGmS4S1KDHJZR8zxhp5XIcFeTDHStdIa7mmGgt6Wfv09PtM7NcNeS4p2L0mh4QlWSGmTPXdKy4vBbfwx3LZq5/lHONcwy1/oO0Wg2fi4+yXDXvJbyOLi9OM1nKXxOJ8Fw18QZ0NLojS3ck1wE/CNwEvCvVbV9XO+1EixG76Of9xj08jRpKRn0M36if2tL/TeCsYR7kpOAfwb+GDgIPJNkZ1XtHcf7tWpcITmqEJeWqkE/vy12WsbVcz8X2F9VPwNI8gCwGRh5uJ/oD3yY/00HPfk37v30s/+F7HNUH9jl9sGXFqPz1I9x9fpTVaPfafJV4KKq+utu/mrgi1V1fc86W4At3ezvA6+OvJDBrAJ+MeEaFoPH2ZaVcpywco51kOP83aqamm3BxE6oVtUOYMek3v94SfZU1fSk6xg3j7MtK+U4YeUc66iOc1x3qB4C1vXMn9m1SZIWwbjC/RlgQ5Kzk/wWcCWwc0zvJUk6zliGZarqWJLrgf9k5lLIu6vq5XG81wgtmSGiMfM427JSjhNWzrGO5DjHckJVkjRZPhVSkhpkuEtSgwz3TpK/S/JCkueTPJbkM5OuaVySfCvJK93xPpLktEnXNA5J/iLJy0k+SNLcJXRJLkryapL9SbZNup5xSXJ3kiNJXpp0LeOSZF2SJ5Ls7T6zNwy7T8P9Y9+qqs9X1Sbg34G/nXA94/Q48AdV9Xngv4GbJ1zPuLwE/Dnw5KQLGbWeR3xcDGwErkqycbJVjc09wEWTLmLMjgE3VdVG4Dxg67B/n4Z7p6re6Zn9FNDsmeaqeqyqjnWzTzFzH0JzqmpfVU36zudx+egRH1X1f8CHj/hoTlU9Cbw16TrGqaoOV9Vz3fS7wD5g7TD79JG/PZLcDlwDvA18ZcLlLJa/An4w6SI0sLXA6z3zB4EvTqgWjVCS9cA5wNPD7GdFhXuSHwG/M8uiW6vq0aq6Fbg1yc3A9cBti1rgCM13rN06tzLz6+B9i1nbKPVznNJykeRU4CHgxuNGEwa2osK9qv6oz1XvA3axjMN9vmNN8pfAnwIX1DK+2WGAv9PW+IiPxiQ5mZlgv6+qHh52f465d5Js6JndDLwyqVrGrfsilb8B/qyq3pt0PVoQH/HRkCQB7gL2VdUdI9nnMu60jVSSh5h59PAHwGvAN6qqyZ5Qkv3AKcAvu6anquobEyxpLJJcDvwTMAX8L/B8VV040aJGKMklwD/w8SM+bp9sReOR5H7gfGYehfsmcFtV3TXRokYsyZeB/wJeZCaDAG6pql0L3qfhLkntcVhGkhpkuEtSgwx3SWqQ4S5JDTLcJalBhrskNchwl6QG/T/f+Nm+J6yvwAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"#bins = [-3,-2,-1,0,1,2,3]\n",
"#bins = np.linspace(-3,3,100)\n",
"plt.hist(values[:,0],bins=100);"
]
},
{
"cell_type": "code",
"execution_count": 65,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD4CAYAAAAXUaZHAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAAANx0lEQVR4nO3df+hd9X3H8edrzvWPKaiYZS6GRUpWSMcWyxfn6P5wc1v9MRYdm+gfNusc6R8RFISh7R/tP4XAVsvKNkc6xRScTlAxrHZtGgQpTOs3Emxi6hraiAnRfDtHFYSO2Pf+yIm7xm/y/XF/nO/3c58PuNxzPuece9+HfO/rfvI5P26qCklSW36h7wIkSaNnuEtSgwx3SWqQ4S5JDTLcJalBv9h3AQCXXnppbdiwoe8yJGlV2bdv30+qas18y1ZEuG/YsIHZ2dm+y5CkVSXJa2db5rCMJDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkNMtwlqUGGuyQ1aEVcoSqN2oZ7v/H+9JEdN/ZYidQPe+6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXI89zVjMFz26VpZ89dkhq0YLgnWZ/k2SSvJDmY5K6u/YtJjiXZ3z1uGNjmviSHk7ya5FPj3AFJ0octZljmJHBPVb2U5EJgX5I93bKvVNXfDa6cZBNwK/Bx4NeA7yT5jap6b5SFS5LObsGee1Udr6qXuul3gEPAunNssgV4rKp+VlU/Bg4DV42iWEnS4ixpzD3JBuBK4IWu6c4kLyd5KMnFXds64PWBzY5y7i8DSdKILTrck1wAPAHcXVVvAw8AHwU2A8eBLy/ljZNsSzKbZHZubm4pm0qSFrCoUyGTnM+pYH+kqp4EqKo3B5Z/Dfj3bvYYsH5g88u7tg+oqp3AToCZmZlaTvHSUnkrYE2LxZwtE+BB4FBV3T/QftnAajcDB7rp3cCtST6S5ApgI/C90ZUsSVrIYnrunwRuB76fZH/X9jngtiSbgQKOAJ8FqKqDSR4HXuHUmTbbPVNGkiZrwXCvqu8CmWfRM+fY5kvAl4aoS5I0BK9QlaQGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIn9nTquZP60nzs+cuSQ0y3CWpQYa7JDXIcJekBnlAVVPrzIOx/niHWmK4q3meUaNpZLhr1TGspYU55i5JDTLcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIe8tIncF71niHSK129twlqUGGuyQ1aMFwT7I+ybNJXklyMMldXfslSfYk+WH3fHHXniRfTXI4yctJPjHunZAkfdBieu4ngXuqahNwNbA9ySbgXmBvVW0E9nbzANcDG7vHNuCBkVctSTqnBcO9qo5X1Uvd9DvAIWAdsAXY1a22C7ipm94CfL1OeR64KMlloy5cknR2SxpzT7IBuBJ4AVhbVce7RW8Aa7vpdcDrA5sd7drOfK1tSWaTzM7NzS21bknSOSw63JNcADwB3F1Vbw8uq6oCailvXFU7q2qmqmbWrFmzlE0lSQtYVLgnOZ9Twf5IVT3ZNb95erilez7RtR8D1g9sfnnXJkmakMWcLRPgQeBQVd0/sGg3sLWb3go8PdD+6e6smauBnw4M30iSJmAxV6h+Ergd+H6S/V3b54AdwONJ7gBeA27plj0D3AAcBt4FPjPKgiVJC1sw3Kvqu0DOsvjaedYvYPuQdUkfMHhrAEkL8wpVSWqQ4S5JDTLcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIcJekBhnuktQgw12SGmS4S1KDDHdJatBifmZP6sVK+fWlwTqO7Lixx0qkxbPnLkkNMtwlqUGGuyQ1yDF3aR4rZbxfWi7DXSuKoSqNhsMyktQgw12SGmS4S1KDDHdJapDhLkkN8mwZaQm8FYFWC3vuktSgBcM9yUNJTiQ5MND2xSTHkuzvHjcMLLsvyeEkryb51LgKlySd3WJ67g8D183T/pWq2tw9ngFIsgm4Ffh4t80/JTlvVMVKkhZnwXCvqueAtxb5eluAx6rqZ1X1Y+AwcNUQ9UmSlmGYMfc7k7zcDdtc3LWtA14fWOdo1/YhSbYlmU0yOzc3N0QZkqQzLTfcHwA+CmwGjgNfXuoLVNXOqpqpqpk1a9YsswxJ0nyWFe5V9WZVvVdVPwe+xv8PvRwD1g+sennXJkmaoGWFe5LLBmZvBk6fSbMbuDXJR5JcAWwEvjdciZKkpVrwIqYkjwLXAJcmOQp8AbgmyWaggCPAZwGq6mCSx4FXgJPA9qp6byyVS5LOKlXVdw3MzMzU7Oxs32VoBVit93P3alX1Icm+qpqZb5lXqEpSgwx3SWqQ4S5JDTLcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoP8DVX1brVelSqtZPbcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQV6hql54Vao0XvbcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoM8FVIagcFTO4/suLHHSqRT7LlLUoMMd0lq0ILhnuShJCeSHBhouyTJniQ/7J4v7tqT5KtJDid5Ocknxlm8JGl+i+m5Pwxcd0bbvcDeqtoI7O3mAa4HNnaPbcADoylTkrQUC4Z7VT0HvHVG8xZgVze9C7hpoP3rdcrzwEVJLhtRrZKkRVrumPvaqjreTb8BrO2m1wGvD6x3tGuTJE3Q0AdUq6qAWup2SbYlmU0yOzc3N2wZkqQByw33N08Pt3TPJ7r2Y8D6gfUu79o+pKp2VtVMVc2sWbNmmWVIkuaz3HDfDWztprcCTw+0f7o7a+Zq4KcDwzeSpAlZ8ArVJI8C1wCXJjkKfAHYATye5A7gNeCWbvVngBuAw8C7wGfGULNWEa/clPqxYLhX1W1nWXTtPOsWsH3YoiRJw/EKVUlqkOEuSQ0y3CWpQd7yVxojDyirL/bcJalBhrskNchhGU3M4BCFpPGy5y5JDTLcJalBhrskNchwl6QGGe6S1CDPlpFGzLOCtBLYc5ekBhnuktQgh2WkCfE+M5oke+6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIcJekBhnuktQgr1CVeuDVqho3e+6S1CDDXZIaZLhLUoMcc9fI+WMVUv+GCvckR4B3gPeAk1U1k+QS4N+ADcAR4Jaq+p/hypQkLcUohmV+v6o2V9VMN38vsLeqNgJ7u3lJ0gSNY8x9C7Crm94F3DSG95AkncOw4V7At5PsS7Kta1tbVce76TeAtfNtmGRbktkks3Nzc0OWIUkaNOwB1d+rqmNJfgXYk+QHgwurqpLUfBtW1U5gJ8DMzMy860iSlmeonntVHeueTwBPAVcBbya5DKB7PjFskZKkpVl2uCf55SQXnp4G/hg4AOwGtnarbQWeHrZISdLSDDMssxZ4Ksnp1/nXqvqPJC8Cjye5A3gNuGX4MiVJS7HscK+qHwG/PU/7fwPXDlOUJGk4XqGqkfCqVGll8d4yktQge+5Sz7y3u8bBnrskNcieu7RC2aPXMOy5S1KDDHdJapDDMtIq4BCNlsqeuyQ1yJ67ls0Ll6SVy3CXVhC/MDUqDstIUoPsuWtJ7FlKq4PhLq0ynjmjxXBYRpIaZLhLUoMMd0lqkGPuWpAHUVcfx+Vlz12SGmS4S1KDDHdJapDhLkkN8oCq1AgPfGuQPXdJapA9d2kVs7eus7HnLkkNsueuedkjbIcXNE0nw33K+cHXmc78YvfvYnUy3PU+e+vt88t8ehju0pSaRND7ZdKfsYV7kuuAvwfOA/6lqnaM672mzVI/MPbItZBz/Y2cbdng354hvvKMJdyTnAf8I/BHwFHgxSS7q+qVcbzfNPNDpdViMV8Sw7ymf/8fNK6e+1XA4ar6EUCSx4AtwMjD/Vw9jnH8Yw/Tax7H+lJfzvbZW+r/FJe6/jCfo5UyFDWJOlJVo3/R5M+B66rqr7v524Hfqao7B9bZBmzrZj8GvDryQhbnUuAnPb13n9zv6TOt+97yfv96Va2Zb0FvB1Sraiews6/3Py3JbFXN9F3HpLnf02da931a93tcV6geA9YPzF/etUmSJmBc4f4isDHJFUl+CbgV2D2m95IknWEswzJVdTLJncC3OHUq5ENVdXAc7zUCvQ8N9cT9nj7Tuu9Tud9jOaAqSeqXd4WUpAYZ7pLUIMMdSPK3SX6Q5OUkTyW5qO+aJiHJXyQ5mOTnSZo/VSzJdUleTXI4yb191zMpSR5KciLJgb5rmaQk65M8m+SV7u/8rr5rmiTD/ZQ9wG9W1W8B/wXc13M9k3IA+DPgub4LGbeBW2JcD2wCbkuyqd+qJuZh4Lq+i+jBSeCeqtoEXA1sn6J/c8MdoKq+XVUnu9nnOXVefvOq6lBV9XVl8KS9f0uMqvpf4PQtMZpXVc8Bb/Vdx6RV1fGqeqmbfgc4BKzrt6rJMdw/7K+Ab/ZdhEZuHfD6wPxRpuiDPu2SbACuBF7ouZSJmZr7uSf5DvCr8yz6fFU93a3zeU79V+6RSdY2TovZb6llSS4AngDurqq3+65nUqYm3KvqD8+1PMlfAn8CXFsNnfy/0H5PEW+JMYWSnM+pYH+kqp7su55JcliG939Y5G+AP62qd/uuR2PhLTGmTJIADwKHqur+vuuZNMP9lH8ALgT2JNmf5J/7LmgSktyc5Cjwu8A3knyr75rGpTtgfvqWGIeAx1fwLTFGKsmjwH8CH0tyNMkdfdc0IZ8Ebgf+oPtc709yQ99FTYq3H5CkBtlzl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQf8HJXuJ/flNKXMAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plt.hist(values[:,-1],bins=100);"
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"Text(0, 0.5, 'Number of Instances')"
]
},
"execution_count": 66,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYkAAAEKCAYAAADn+anLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAAAik0lEQVR4nO3de5xVdb3/8dcbRSkhMUAPchEUPYqWo42GWV7z2knFNPV0UPNC55ecvORRzNNPsviJx5LqeDJJNOio6NEMKy2RUOvxEA0Jb5A6ouAQecHwloCDn98fa824GfeeWTOz96w9e97Px2M/Zq/vWnutz+KyP7O+37U+X0UEZmZmxfTJOwAzM6teThJmZlaSk4SZmZXkJGFmZiU5SZiZWUmb5x1AOQ0ePDhGjRqVdxhmZj3Ko48++mpEDCm2rqaSxKhRo1i0aFHeYZiZ9SiSVpRa5+4mMzMryUnCzMxKcpIwM7OSampMwsystXfffZfGxkbWrVuXdyi569evH8OHD6dv376ZP+MkYWY1rbGxkQEDBjBq1Cgk5R1ObiKCNWvW0NjYyOjRozN/zt1NZlbT1q1bx6BBg3p1ggCQxKBBgzp8ReUkYWY1r7cniGad+XNwkjAzs5I8JmFmvcr0ec+UdX/nH7ZLm+vXrl3LzTffzFe/+tUO7XflypWMHTuWKVOmcOGFFwLwm9/8hnPPPZeNGzdy1llnMXny5E7HnZWvJMwqbPq8Z1pe1vusXbuWH/3oRx3+3AUXXMBRRx3Vsrxx40bOOecc7rnnHpYuXcott9zC0qVLyxlqUb6SMDOroMmTJ/Pcc89RV1fHPvvsw9NPP80bb7xBU1MT1157LZ/5zGc+8Jlf/OIXjB49mq222qql7ZFHHmHMmDHsuOOOAJx88snMnTuXsWPHVjR+X0mYmVXQtGnT2GmnnViyZAm77rorRxxxBEuWLOGxxx6jrq7uA9u/9dZbXHnllVx22WWbtK9atYoRI0a0LA8fPpxVq1ZVOnxfSZiZdZd99tmHM844g3fffZfjjjuuaJKYMmUK559/Pv379+/+AItwkjAz6yYHHHAADz74IL/+9a85/fTTueCCCxgwYADf+ta3ALj++ut5+OGHuf3227noootYu3Ytffr0oV+/fnziE5/gxRdfbNlXY2Mjw4YNq3jMThJmZhU0YMAA3nzzTQBWrFjB8OHDOfvss1m/fj2LFy/m+9//PuPHj2/Z/ve//33L+ylTptC/f38mTZpEU1MTzz77LM8//zzDhg1jzpw53HzzzRWP30nCzHqV9m5ZLbdBgwax//77s8cee/D222+z1VZb0bdvX/r378/s2bMz72fzzTfnmmuu4YgjjmDjxo2cccYZ7L777hWMPD1uxY9gZtbLdfY3/ilTpmyyfPTRR3P00UeXIaLsfHeTmZmV5CRhZmYlOUmYmVlJThJmZlaSk4SZmZXkJGFmZiV12y2wkvoBDwJbpse9PSIukzQamAMMAh4FJkTEBklbArOBTwBrgJMi4oXuitfMatSCK8q7v4MvaXN1R0uFz5s3j8mTJ7Nhwwa22GILrrrqKg455BAANmzYwKRJk7j//vvp06cPU6dO5Qtf+ALr16/n1FNP5dFHH2XQoEHceuutjBo1qqtnBnTvlcR64JCI2BOoA46UNA64EpgeEWOAvwFnptufCfwtbZ+ebmdWM1xCvHfoaKnwwYMH88tf/pInnniCWbNmMWHChJZ1U6dOZdttt+WZZ55h6dKlHHjggQDMnDmTbbbZhoaGBs4//3wuvvjissXfbUkiEm+li33TVwCHALen7bOA49L3x6bLpOsPlecgNLMeprBU+Nlnn80BBxxAXV0de+yxxyYlOJrttddebL/99gDsvvvuvPPOO6xfvx6AG264gUsuSa5c+vTpw+DBgwGYO3cup512GgAnnHAC8+fPJyLKEn+3jklI2kzSEuBlYB7wHLA2IprSTRqB5opVw4AXAdL1r5N0SbXe50RJiyQteuWVVyp8BmZmHdPRUuGF7rjjDvbee2+23HJL1q5dC8A3v/lN9t57b0488UReeuklYNMy4ptvvjlbb701a9asKUv83ZokImJjRNQBw4F9gV3LsM8ZEVEfEfVDhgzp6u7MzCpmn3324cYbb2TKlCk88cQTDBgwoOS2Tz31FBdffDHXXXcdAE1NTTQ2NvKpT32KxYsXs99++7VMa1pJudzdFBFrgQXAfsBASc0D6MOB5lk0VgEjANL1W5MMYJv1WB6H6N2aS4UPGzaM008/ndmzZ3PnnXdSV1dHXV0dixYtApIy4OPHj2f27NnstNNOQFIo8MMf/jDHH388ACeeeCKLFy8GYNiwYS1lxJuamnj99dcZNOgDHS+d0m1JQtIQSQPT9x8CDgOWkSSLE9LNTgPmpu/vSpdJ1/8uytXJZmbWTVqXCt9uu+04++yzOeuss1i8eDHjx49nyZIlLFmyhPr6etauXcvnPvc5pk2bxv7779+yH0l8/vOf5/777wdg/vz5LVOXHnPMMcyalQzh3n777RxyyCGUawi3O6vADgVmSdqMJDndFhG/krQUmCPpO8CfgJnp9jOBn0lqAF4DTu7GWM2sVrVzy2q5dbRU+DXXXENDQwOXX345l19+OQD33nsv2267LVdeeSUTJkzgvPPOY8iQIdx4440AnHnmmUyYMIExY8bw0Y9+lDlz5pQtftXSL+f19fXRfLlmlqeOdid19xwHvcmyZcvYbbfd8g6jahT785D0aETUF9veT1ybmVlJThJmZlaSk4SZ1bxa6lbvis78OThJmFlN69evH2vWrOn1iSIiWLNmDf369evQ5zp9d5OkMUBjRKzr7D7MzCpt+PDhNDY24ooMScIcPnx4hz6TKUlI+n/A0xExK62fdC9wKPC6pCMj4uEOR2tm1g369u3L6NGj8w6jx8p6JfEl4KT0/VEkVVzHpe3TgIPLHplZL1J4y6xvh7VqkjVJbEdSfA/gaJIH4R6R9BrgBxPMzGpU1oHrNcAO6fvDgfnp+80Bl+82M6tRWa8k7gBulvQM8FHgt2l7HdBQgbjMzKwKZE0SFwArgJHARRHxdto+FLi2EoGZmVn+MiWJdNKf7xVpn172iMzMrGpkfphO0sckXSPpHklD07bjJO1VufDMzCxPmZKEpMOBP5JMKXoI8KF01U7AZZUJzczM8pb1SuLbwAURMR7YUNB+P8k0pGZmVoOyJok9gLuLtL9GcreTmRUYt3IG41bOyDsMsy7LmiReI+lqam1v3n/IzszMakzWJHEzcJWk4UAAm0s6EPgu8MH598zMrCZkTRL/ATxP8qxEf2Ap8DvgD8DUyoRmZmZ5y/qcxLvAlyR9k6SLqQ/wp4h4tpLBmZlZvrKWCt8C6BMRy4HlBe39gPciYkPJD5uZWY+VtSzH/wIPAFe3av9X4CDguPKFZNYzFZb7HpdjHGbllDVJ7A9cWqR9HvCN8oVj1nP5llerRVkHrj8MNBVpfw8YkGUHkkZIWiBpqaSnJJ2btk+RtErSkvR1dMFnLpHUIOlpSUdkjNXMzMok65XE48ApfLAExz8DT2bcRxPw9YhYLGkA8Kikeem66RHx3cKNJY0FTgZ2B7YH7pO0S0RszHg8MzProqxJ4nJgrqQxJLe+QjLH9YnA+Cw7iIjVwOr0/ZuSllH8Ab1mxwJzImI98LykBpISIA9ljNnMzLooU3dTRNwNfJ5kdrofpq+RwDER8auOHlTSKGAv4OG0aZKkxyXdIGmbtG0Y8GLBxxopklQkTZS0SNKiV155paOhmJlZGzKXCo+I30TEpyNiq/T16Yi4p6MHlNSfZKa78yLiDZJJi3YimeVuNUXmrWgnrhkRUR8R9UOGDOloOGbdxvWcrCfK2t3UQtJAWiWXiHgt42f7kiSImyLi5+lnXypY/xOg+cpkFTCi4OPD0zazmlZ4K+35h+2SYyRm2eeT2CGdbOgdYA3wSvp6Nf2ZZR8CZgLLIuLqgvahBZuN5/2B8LuAkyVtKWk0sDPwSJZjmZlZeWS9krgRGAicCfyFpMhfR+0PTACekLQkbfsGcIqkunSfLwBfAYiIpyTdRlInqgk4x3c2mZl1r6xJYl9gXERkvd31AyLiD4CKrCo2T0XzZ6biAoJmZrnJOnD9PLBlJQMxM7PqkzVJnAtckT4nYWZmvUTW7qa5JFcST0taT6sSHRHxkXIHZmZm+cuaJCZVNAozM6tKWScdmlXpQMzMrPp05mG6fwC2KGyLiJVli8isp1lwRd4RmFVM1pnptiap1/RFWiWI1GblDMrMzKpD1rubvgvsSTID3TqSEuH/TlJ076SKRGZmZrnL2t10FHBKRPxe0kbg0Yi4VdJqkiekb69YhGZmlpusSWIgsCJ9/zowCGggmdvh+vKHZVa7CivBLhw5McdIzNqXNUk8B+wIrASWkRTeewQ4HshUAdasN3JpcOvpsiaJnwIfB+4HppGU855EMqZxbiUCM6tqvqPJeomsz0lML3j/O0m7AvXAsxHxRKWCMzOzfGW9BfZU4NZ0vunm5yJWStpC0qkRMbuSQZpVq4eWr8k7BLOKynoL7I3A1kXaB6TrzMysBmVNEqL4REMjSe52MjOzGtRmd5OkJ0iSQwAPSCqs/roZsANtTBpkZmY9W3tjEs0Pye0B/Bp4q2DdBpLpRu8of1hmBjB93jObLJ9/2C45RWK9VZtJIiK+BSDpBWBO88C1mZn1DlnHJO4GWiYWkvQxSd+RdEplwjIzs2qQNUncBnweQNJg4EFgPPBjSV+vUGxmNW/cyhl+KtuqWtYk8XFgYfr+BKAhInYHTiUp8GdmZjUoa5L4EO8PWn8WuCt9vxgYkWUHkkZIWiBpqaSnJJ2btn9U0jxJz6Y/t0nbJemHkhokPS5p7+ynZWZm5ZA1STwLHC9pBHA4cG/avh2wNuM+moCvR8RYYBxwjqSxwGRgfkTsDMxPlyEpT75z+poIXJvxOGZmViZZk8S3gCtJbnldGBEPp+1HAH/KsoOIWB0Ri9P3b5JUkx0GHAs0z6E9i2RiI9L22ZFYCAyUNDRjvGZmVgZZC/z9XNJIYHvgsYJV99GJ5yQkjQL2Ah4GtouI1emqv5JcnUCSQF4s+Fhj2rYaMzPrFllLhRMRLwEvtWp7uMTmJUnqT5JYzouINyQV7i8kFSv/0db+JpJ0RzFy5MiOhmNmZm3InCQknQQcCmxLq26qiDgm4z76kiSImyLi52nzS5KGRsTqtDvp5bR9FZsOig9P2zYRETOAGQD19fUdSjBmZta2TGMSkq4C/gcYRTJQvabVK8s+BMwElkXE1QWr7gJOS9+fBswtaD81vctpHPB6QbeUmZl1g6xXEqcCp0TE7e1uWdr+wATgCUlL0rZvkMx0d5ukM0nm0f5iuu5u4GiSubT/Dny5C8c2Kw/PSGe9TNYk0QdY0pUDRcQfSEqOF3Noke0DOKcrxzQzs67JegvsDOBfKhmImZlVn6xXEgOBf5Z0GPA48G7hyoj4WpnjMjOzKpA1SYzl/e6mXVut8x1FZmY1KuvDdAdXOhAza1/hJESegMi6Q9YxCTMz64Xam+P6h1l24jEJM7Pa1F5308cy7MNjEmZmNaq9Oa49FmFm1ot5TMLMzEpykjAzs5KcJMzMrCQnCTMzK6lkkpB0g6QB6fsDJGWee8LMzGpDW1/8/0JSyvtNYAFQOCGQWe/RjeXBx62c0fJ+4ciJ3XZcs1LaShIvAP8m6V6SEt/7SfpbsQ0j4sEKxGZmZjlrK0n8O3A9cAnJA3N3ltgugM3KHJeZmVWBkkkiIuYCcyUNBF4DdsfdTWZmvUq7g9ERsVbSwcCzEdHUDTGZVYecxiLMqknWUuEPSNpS0qkkc0sEsBS4OSLWVzJAMzPLT6YkIWkscA+wNfBE2nw2MEXSkRGxrELxmVWdh5avyTsEs26T9WG6H5DMTDcyIj4TEZ8BRgKPAd+vTGhmZpa3rA/I7Q/sExFvNDdExBuSLgUWViQyMzPLXdYriXXAwCLtW6frzKzMxq2c4QFty13WJPFL4CeS9pe0Wfr6NHAdcFeWHaRlPl6W9GRB2xRJqyQtSV9HF6y7RFKDpKclHdGRkzIzs/LImiTOBZ4Ffk9y5bAOeAB4Bjgv4z5+ChxZpH16RNSlr7uhZaD8ZJJnM44EfiTJD+yZmXWzrLfArgWOlTQG2C1tXhYRDVkPFBEPShqVcfNjgTnp7bXPS2oA9gUeyno8s3LyHU3WW3WosmuaFDInhowmpc9fLAK+HhF/A4ax6YB4Y9r2AZImAhMBRo4cWebQzMx6t7znk7gW2AmoA1YD3+voDiJiRkTUR0T9kCFDyhyemVnvlmuSiIiXImJjRLwH/ISkSwlgFTCiYNPhaZuZmXWjXJOEpKEFi+OB5juf7gJOTkuBjAZ2Bh7p7vjMzHq7dsck0hnpJgK/iIi/dPZAkm4BDgIGS2oELgMOklRHUgvqBeArABHxlKTbSOpDNQHnRMTGzh7bzMw6J0sV2CZJVwG/7sqBIuKUIs0z29h+KjC1K8c0qwWerc7ylPXupoXA3sCKCsZiZh0wfd4zLe/PP2yXHCOxWpY1SfwE+J6kHYBHgbcLV0bE4nIHZmZm+cuaJG5Of15dZJ2nLzUzq1FZk8ToikZhZmZVKWtZDo9FmJn1Qpmfk5B0lKRfSVoqaUTadpakQysXnpmZ5SlTkpD0JeA2kkqwo4G+6arNgIsqE5qZmeUt65jERcDZETFH0lkF7QuBy8sflllOFlzR8taVX82ydzftTPEy3W8BHylfOGZmVk2yJom/AMWe1jkAeK584ZiZWTXJmiRmAD+UtH+6PELSacB/kpT7NjOzGpT1Ftj/lLQ1MA/oBywA1gPfjYj/rmB8ZmaWo8wz00XEpZKmAmNJrkCWRsRbFYvMzMxy16HpS0lKcKxL37t0t5lZjcuUJCRtCVxJMt/DFoCA9ZJmABdHxLq2Pm9W9QpufTWz92W9krgWOBw4i/dvhd0PuAIYAJxR/tDMzCxvWZPEicDxETGvoG25pJeBO3CSMDOrSVlvgX0bWFWkfRXwTvnCMTOzapI1SfwXcJmkDzU3pO+/ma4zM7MaVLK7SdJdrZoOAlZJejxd/lj6+a0qE5qZmeWtrTGJ1tXN7mi1/HyZYzEzsypTMklExJe7MxAza9+4lTMAWDhy4ibt0+c90/L+/MOKlVkz65zMkw6ZmVnvk3XSoW0k/UDS45L+KunlwlfGfdyQbv9kQdtHJc2T9Gz6c5u0XZJ+KKkhPebenTs9MzPriqzPScwGdgdmAS+RlOfoqJ8C16T7ajYZmB8R0yRNTpcvBo4imcNiZ+CTJA/zfbITxzQzsy7ImiQOAg6MiMWdPVBEPChpVKvmY9N9Q5KA7idJEscCsyMigIWSBkoaGhGrO3t8MzPruKxJ4jkqM36xXcEX/1+B7dL3w4AXC7ZrTNs+kCQkTQQmAowcObICIVpv4ilLzTaV9Yv/XOAKSXtK2qwSgaRXDR3uxoqIGRFRHxH1Q4YMqUBkZma9V9Yk0QB8CFgMbJC0sfDVheO/JGkoQPqzeRB8FTCiYLvhFC8LYtZxC65w1VezjLJ2N90CbA18jc4PXBdzF3AaMC39ObegfZKkOSQD1q97PMLMrPtlTRL1wL4R8WS7W5Yg6RaSQerBkhqBy0iSw22SzgRWAF9MN78bOJrkCubvgB/ss4pofght3EqPRZgVkzVJLAU+0pUDRcQpJVYdWmTbAM7pyvHMzKzrso5J/AdwtaTPStoufQiu5VXJAM3MLD9ZryTuTn/ey6bjEUqXK3LHk5m1r1Q9J7NyyJokDq5oFGZmVpUyJYmIeKDSgZh1uwVXeMDarB2ZkkR7Bfa6Uq7DzMrLZcOtnLJ2Ny0iGXtQQVvh2ITHJMzMalDWJDG61XJfYC/gUuCSskZkZmZVI+uYxIoizQ2SXid5KO6eskZlZmZVIeuVRCnPA3VliMPMOqD5tlezSss6cN36gTkBQ4EpwNNljsmsonpTOXAPYltXZb2SeJUPFvUTyZwPJ5U1IjPrlMKrCz9YZ+XS2Yfp3gNeARoioqm8IZmZWbXww3RmZlZSm0kia/G+iHitPOGYmVk1ae9KothYRGuRYT9mZtYDtffl3lZhvyNJ5r72mISZWY1qM0kUG4uQtBdwFfAZ4Drg25UJzczM8pZ10iEkjZZ0M/AIsAYYGxFfi4hXKhadmZnlqt0kIWmQpB8Afwb+AfhURJwUEc9VPDoz65RxK2f4qWwrizaThKRLgeeAA4FjI+KQiPhjt0RmZma5a2/g+tvAO0Aj8FVJXy22UUQcU+7AzMwsf+0lidm0fwusWdUrrGE0Lsc4zHqa9u5uOr07gpD0AvAmsBFoioj69EG+W4FRwAvAFyPib90Rj9Ue98+bdU41PQR3cES8WrA8GZgfEdMkTU6XL84nNOuJfPVg1nWZb4HNwbHArPT9LOC4/EIxM+udquVKIoB7JQVwXUTMALaLiNXp+r8C2xX7oKSJwESAkSNHdkesZj2S55awzqiWJPHpiFglaVtgnqQ/F66MiEgTyAekCWUGQH19vQfZzczKqCq6myJiVfrzZeBOYF/gJUlDAdKfL+cXoZlZ75T7lYSkrYA+EfFm+v5w4HLgLuA0YFr6c25+UZrVFnc9WVa5JwmSsYY7JUESz80R8RtJfwRuk3QmsAL4Yo4xmpn1SrkniYhYDuxZpH0NcGj3R2S1xM9HmHVNVYxJmJlZdcr9SsKsnAr72m3TK6mFIyfmGIn1VE4SZr2ME4d1hLubzMysJCcJs15s3MoZsOCKvMOwKuYkYWZmJXlMwmqOb3s1Kx8nCeuRfBdTx5VKng8tX8PCpuTPs/Dpaz+VbeDuJjMza4OvJKxmuJup85r/7B6a6dtibVO+kjAzs5J8JWE9hschqoPHKnoXX0mYmVlJvpKwHs3jEN2k+YG7gy/JNw7rdk4SVtXcxWSWL3c3mZlZSb6SMLN2PbR8DUDLQ3fWezhJmFlRHu8xcJKwblZqjMG3UlaPjiQH3w5b+5wkrCza+rLo6OCzB6vNqoeThFWFjiYGd4Xkw7Pa9T5OElb1mr+Y/KVU3QoT/biVM9hvx0HJwsGXuFuqB3OS6OUqMUZQqe4iXz1UFyfv3qHqk4SkI4EfAJsB10fEtJxDqqju+I2rK1/ilR4v8BdPz1OqC6r1bbPFKs2ev/kdLdtPb/pCy3b77TjIT3dXiapOEpI2A/4bOAxoBP4o6a6IWJpvZD1DVxJOuZNBR/uyfdXQMxX7eyvn36W7rbpfVScJYF+gISKWA0iaAxwLVDRJtPUF2ZUv2079o05r5jT/Vgaw35nf7fh+isj6W3te21ntakkczeMWbJpMHlq+BpZf+MHPFS4sGLTp9gVarlQO26Xl/1DzlUrzsT5wtVLu+lRt7a95XTmPVyGKiLxjKEnSCcCREXFWujwB+GRETCrYZiLQ/G3zj8DTnTzcYODVLoRbTXwu1alWzqVWzgN8Ls12iIghxVZU+5VEuyJiBtDl61lJiyKivgwh5c7nUp1q5Vxq5TzA55JFtRf4WwWMKFgenraZmVk3qPYk8UdgZ0mjJW0BnAzclXNMZma9RlV3N0VEk6RJwG9JboG9ISKeqtDhaul2Gp9LdaqVc6mV8wCfS7uqeuDazMzyVe3dTWZmliMnCTMzK8lJooCkb0t6XNISSfdK2j7vmDpL0lWS/pyez52SBuYdU2dJOlHSU5Lek9TjbleUdKSkpyU1SJqcdzydJekGSS9LejLvWLpK0ghJCyQtTf9tnZt3TJ0hqZ+kRyQ9lp7Ht8p+DI9JvE/SRyLijfT914CxEfGvOYfVKZIOB36XDv5fCRARF+ccVqdI2g14D7gOuDAiFuUcUmZpaZlnKCgtA5zSE0vLSDoAeAuYHRF75B1PV0gaCgyNiMWSBgCPAsf1tL8XSQK2ioi3JPUF/gCcGxELy3UMX0kUaE4Qqa2AHptBI+LeiGhKFxeSPGPSI0XEsojo7JP0eWspLRMRG4Dm0jI9TkQ8CLyWdxzlEBGrI2Jx+v5NYBkwLN+oOi4Sb6WLfdNXWb+3nCRakTRV0ovAl4D/m3c8ZXIGcE/eQfRSw4AXC5Yb6YFfRrVM0ihgL+DhnEPpFEmbSVoCvAzMi4iynkevSxKS7pP0ZJHXsQARcWlEjABuAia1vbd8tXcu6TaXAk0k51O1spyLWblJ6g/cAZzXqiehx4iIjRFRR9JbsK+ksnYFVvXDdJUQEZ/NuOlNwN3AZRUMp0vaOxdJpwP/BBwaVT741IG/l57GpWWqVNqHfwdwU0T8PO94uioi1kpaABwJlO3mgl53JdEWSTsXLB4L/DmvWLoqnazpIuCYiPh73vH0Yi4tU4XSAd+ZwLKIuDrveDpL0pDmOxclfYjkBomyfm/57qYCku4gKTf+HrAC+NeI6JG/9UlqALYEmgvtL+zBd2qNB/4LGAKsBZZExBG5BtUBko4Gvs/7pWWm5htR50i6BTiIpCT1S8BlETEz16A6SdKngd8DT5D8fwf4RkTcnV9UHSfp48Askn9bfYDbIuLysh7DScLMzEpxd5OZmZXkJGFmZiU5SZiZWUlOEmZmVpKThJmZleQkYdaDSHpB0oV5x2G9h5OE1SRJP5UURV5lq46Zk32AH+UdhPUeva4sh/Uq9wETWrVtqNTBJG2RVnqtmIh4pZL7N2vNVxJWy9ZHxF9bvV6TdKCkdyUd1LyhpK9IekPSjuny/ZJ+LOkHkv6Wvq6S1KfgMy9ImpJOxrOWtIiipE9JekDS3yWtknStpI8UfO4ASQslvSXp9XTSmD3SdVtL+lk6uc86ScslndfqmBcWLI9UMqnUm+nr55KGF6yfkhZKPFnSc+k2v5A0uAJ/3laDnCSs14mIB4CrgJ9J2kbSrsDVwL9FxPKCTb9E8n9kP+ArwETgvFa7u4CkVk498A1JHwPuJanPtCdwPFAH3AAgaXNgLsnkMHsCnyQp2bEx3d93gI+RFGb8R5Iy70VLw6QJay6wHXBw+toe+EVam6jZKOAkYDxwOElZ7B5ZGsS6n7ubrJYdKemtVm3/nc7QdxlJMbSZJF+iv4qIWa22XQ18La2g+2dJu5AkhcKCcA9ExH82L0iaDdwaEd8raPs/wJ8kbUtStn0g8MuIeC7dpLAg2w7A4oh4JF1e0cb5HQp8HNgpIl5Ij/XPQEO67r50u82B0yPi9XSbGcCX29ivWQsnCatlD5L89l9oLUBEvJt+oT5FMlnLIUU+v7BVifWHgG+rYJpboPVUqp8Axkg6qaCt+bf6nSLiIUk/BX4raT4wH7g9Ilam21wL3C7pE8A8kmTyQInz2w34S3OCSM9ruaS/AGN5P0msaE4Qqb8A25bYp9km3N1ktezvEdHQ6vVqwfpxJP8HBpJUmO2Mt1st9wGuJ+lian7tCewMLAGIiC+TdDM9CBwDPC3piHTdPSRXE98lqbb6a0k3diKuwuT2bpF1/r9vmfgfivVKkkYD1wDnkPzG/j/peEGhT7bq2x9H8pt7WzOYLQZ2L5KcGiLineaNIuKxiLgyIg4C7gdOK1j3akT8LCJOB84ETpO0ZZFjLQO2VzL9ZvN57UgyLrG0nT8Cs0ycJKyWbSnpH1q9hkjaDPgZyXjCdcBZJLPHtZ6FcHvg+5L+UdIJwL8D09s55pUkU0j+WNJeksZI+idJ10GSnCRNS++A2kHSwSTjCkvT9ZdLOk7SzpJ2Ixn4Xh4R64sc6z7gceAmSfWS6knusFoM/K7Df1pmRXhMwmrZZ0kGnwutAq4DxpDcRURErJF0GnC3pN9GxB/SbW8imczlYZIumpm0kyQi4nFJB5DcpfRA+vnlwJ3pJn8HdgH+l/cn77mJJLkArCe582g0sA5YCHy+xLFCyRzgPwQWpM33kdyl5YlirCw86ZBZEZLuB56MiEl5x2KWJ3c3mZlZSU4SZmZWkrubzMysJF9JmJlZSU4SZmZWkpOEmZmV5CRhZmYlOUmYmVlJ/x/DUQ3pJgVtBQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"bins = np.linspace(-3,3,100)\n",
"plt.hist(values[:,0],bins=bins, alpha=0.5,label=\"ts-40\")\n",
"plt.hist(values[:,-1],bins=100,alpha=0.5,label=\"ts-260\")\n",
"plt.legend(loc=\"best\");\n",
"plt.xlabel(\"Expression\", size=14)\n",
"plt.ylabel(\"Number of Instances\", size=14)"
]
},
{
"cell_type": "code",
"execution_count": 67,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXsAAAD4CAYAAAANbUbJAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAAAOzElEQVR4nO3dbYxc1X3H8e+v5KFSkxaoXdc1Jk5Tt5KRWhNtKVKqhoq0EJBqIkUUpIAbUTkvQEpU3jjJi0SVkNyHQBupRXUKiqlCCCFBWA1NCy5SGqk8rCki2JTgJKbYNfYmoQSVitbw74u9Tib22jO7M7Oz6/P9SKO5c+bcmb+PZ3979sydO6kqJEmnt5+YdAGSpPEz7CWpAYa9JDXAsJekBhj2ktSAN0y6AIAVK1bUunXrJl2GJC0ru3fv/m5VrRyk75II+3Xr1jE9PT3pMiRpWUny3KB9XcaRpAYY9pLUAMNekhpg2EtSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGLIlP0EotWLf1Kz/c3r/t8glWohY5s5ekBhj2ktQAw16SGmDYS1IDDHtJaoBH40gT5lE6WgzO7CWpAYa9JDXAsJekBrhmLy0hvev3vVzL17Cc2UtSAwx7SWqAYS9JDTDsJakBfcM+ydokDyXZm2RPkg937Z9McjDJE93lsp59PppkX5Jnklwyzn+AJKm/QY7GOQrcWFWPJ3krsDvJA919t1TVn/d2TrIBuAo4D/gF4MEkv1xVr42ycEnS4PrO7KvqUFU93m2/DDwNrDnFLpuAu6rq1ar6DrAPuGAUxUqSFmZea/ZJ1gHnA490TTckeTLJ7UnO6trWAM/37HaAU/9ykCSN2cBhn+QtwJeAj1TVD4BbgXcAG4FDwKfm88RJtiSZTjI9MzMzn10lSfM0UNgneSOzQf+5qvoyQFUdrqrXqup14DP8aKnmILC2Z/dzurYfU1Xbq2qqqqZWrlw5zL9BktRH3zdokwS4DXi6qm7uaV9dVYe6m+8Dnuq2dwJ3JrmZ2Tdo1wOPjrRqaZk72WkRpHEZ5GicdwHXAN9I8kTX9jHg6iQbgQL2Ax8CqKo9Se4G9jJ7JM/1HokjSZPVN+yr6utA5rjr/lPscxNw0xB1SZJGyE/QSlIDDHtJaoDns5eWAb+nVsNyZi9JDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWpAYa9JDXAsJekBhj2ktQAw16SGuApjqVlxtMdayGc2UtSA5zZSyPmzFtLkTN7SWqAYS9JDTDsJakBhr0kNcA3aKUx6n2zVpokw15axjzyR4NyGUeSGmDYS1IDDHtJakDfsE+yNslDSfYm2ZPkw1372UkeSPJsd31W154kn06yL8mTSd457n+EJOnUBpnZHwVurKoNwIXA9Uk2AFuBXVW1HtjV3QZ4L7C+u2wBbh151ZKkeekb9lV1qKoe77ZfBp4G1gCbgB1dtx3AFd32JuCOmvUwcGaS1aMuXJI0uHmt2SdZB5wPPAKsqqpD3V0vAKu67TXA8z27Hejajn+sLUmmk0zPzMzMt25J0jwMHPZJ3gJ8CfhIVf2g976qKqDm88RVtb2qpqpqauXKlfPZVZI0TwOFfZI3Mhv0n6uqL3fNh48tz3TXR7r2g8Dant3P6dokSRMyyNE4AW4Dnq6qm3vu2gls7rY3A/f1tF/bHZVzIfBSz3KPJGkCBjldwruAa4BvJHmia/sYsA24O8l1wHPAld199wOXAfuAV4APjrJgSdL89Q37qvo6kJPcffEc/Qu4fsi6JEkj5CdoJakBnvVSGgFPZaylzpm9JDXAsJekBhj2ktQAw16SGmDYS1IDDHtJaoBhL0kNMOwlqQGGvSQ1wLCXpAYY9pLUAMNekhpg2EtSAzzrpXSa6D3z5v5tl0+wEi1FzuwlqQGGvSQ1wLCXpAYY9pLUAMNekhpg2EtSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIa0Dfsk9ye5EiSp3raPpnkYJInustlPfd9NMm+JM8kuWRchUuSBjfIzP6zwKVztN9SVRu7y/0ASTYAVwHndfv8dZIzRlWsJGlh+oZ9VX0N+P6Aj7cJuKuqXq2q7wD7gAuGqE+SNALDfHnJDUmuBaaBG6vqRWAN8HBPnwNd2wmSbAG2AJx77rlDlCFNRu+XhUhL3ULfoL0VeAewETgEfGq+D1BV26tqqqqmVq5cucAyJEmDWFDYV9Xhqnqtql4HPsOPlmoOAmt7up7TtUmSJmhBYZ9kdc/N9wHHjtTZCVyV5M1J3g6sBx4drkRJ0rD6rtkn+TxwEbAiyQHgE8BFSTYCBewHPgRQVXuS3A3sBY4C11fVa2OpXJoA1+m1XPUN+6q6eo7m207R/ybgpmGKkiSNlp+glaQGGPaS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWpAYa9JDXAsJekBgxzimNJS1TvaR32b7t8gpVoqXBmL0kNMOwlqQGGvSQ1wLCXpAYY9pLUAMNekhpg2EtSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGeCI06TTnSdEEzuwlqQmGvSQ1wGUcqSEu6bTLmb0kNcCwl6QG9A37JLcnOZLkqZ62s5M8kOTZ7vqsrj1JPp1kX5Ink7xznMVLkgYzyMz+s8Clx7VtBXZV1XpgV3cb4L3A+u6yBbh1NGVKkobRN+yr6mvA949r3gTs6LZ3AFf0tN9Rsx4GzkyyekS1SpIWaKFr9quq6lC3/QKwqtteAzzf0+9A13aCJFuSTCeZnpmZWWAZkqRBDH3oZVVVklrAftuB7QBTU1Pz3l9aLL2HK0rL1UJn9oePLc9010e69oPA2p5+53RtkqQJWmjY7wQ2d9ubgft62q/tjsq5EHipZ7lHkjQhfZdxknweuAhYkeQA8AlgG3B3kuuA54Aru+73A5cB+4BXgA+OoWZp7Fy60emmb9hX1dUnueviOfoWcP2wRUmSRstP0EpSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIaYNhLUgP8wnGpUX75eFuc2UtSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIaYNhLUgP8BK0kP03bAGf2ktQAw16SGmDYS1IDXLOXOr3r1tLpxrCX9GOO/6XnG7anB5dxJKkBhr0kNcCwl6QGGPaS1ICh3qBNsh94GXgNOFpVU0nOBr4ArAP2A1dW1YvDlSmNnkffqCWjmNn/dlVtrKqp7vZWYFdVrQd2dbclSRM0jmWcTcCObnsHcMUYnkOSNA/Dhn0B/5Rkd5ItXduqqjrUbb8ArJprxyRbkkwnmZ6ZmRmyDEnSqQz7oarfrKqDSX4OeCDJv/feWVWVpObasaq2A9sBpqam5uwjSRqNoWb2VXWwuz4C3AtcABxOshqguz4ybJGSpOEsOOyT/FSStx7bBn4XeArYCWzuum0G7hu2SEnScIZZxlkF3Jvk2OPcWVVfTfIYcHeS64DngCuHL1MaDQ+3VKsWHPZV9W3g1+Zo/x5w8TBFSaNkwEt+glaSmmDYS1IDDHtJaoBfXiLplHrf8/CLTJYvZ/aS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWpAYa9JDXA4+wlLYjH3y8vzuwlqQGGvSQ1wGUcnZY8rfF4OK7Ll2Gv04ZBJJ2cyziS1ABn9pKG5pE5S59hr2XBMJGG4zKOJDXAsJekBriMo2XHo26WNpfcliZn9pLUAGf2ksbGWf7SYdhrSTEcpPEw7LVkuTYvjY5hL2nRnewX+cn+mvMvvuEZ9horf0ilpcGwl7QoBlmWc3IwPmML+ySXAn8JnAH8bVVtG9dzaTJO9oPpD7XGydfOwqSqRv+gyRnAN4HfAQ4AjwFXV9XeufpPTU3V9PT0yOtY7ub7ol7ID8Ega6e+Uaqlar6v00H6n6zPUvzFkmR3VU0N0ndcM/sLgH1V9e2uoLuATcCcYT+MYf8zBpmdDhO043ixDDtznu/+0lI139fpMK/r4/cd5ud5Er9ExjWzfz9waVX9YXf7GuA3quqGnj5bgC3dzV8Bnhl5IZO3AvjupItYghyXEzkmJ3JMTnT8mLytqlYOsuPE3qCtqu3A9kk9/2JIMj3on1gtcVxO5JicyDE50TBjMq5z4xwE1vbcPqdrkyRNwLjC/jFgfZK3J3kTcBWwc0zPJUnqYyzLOFV1NMkNwD8ye+jl7VW1ZxzPtcSd1stUQ3BcTuSYnMgxOdGCx2Qsb9BKkpYWz2cvSQ0w7CWpAYb9CCU5O8kDSZ7trs+ao8/GJP+aZE+SJ5P8/iRqXUyDjEvX76tJ/ivJ3y92jYshyaVJnkmyL8nWOe5/c5IvdPc/kmTdBMpcVAOMyW8leTzJ0e7zO00YYFz+KMneLkN2JXlbv8c07EdrK7CrqtYDu7rbx3sFuLaqzgMuBf4iyZmLV+JEDDIuAH8GXLNoVS2i7hQifwW8F9gAXJ1kw3HdrgNerKpfAm4B/mRxq1xcA47JfwB/ANy5uNVNzoDj8m/AVFX9KnAP8Kf9HtewH61NwI5uewdwxfEdquqbVfVst/2fwBFgoE/ALWN9xwWgqnYBLy9STYvth6cQqar/BY6dQqRX7zjdA1ycJItY42LrOyZVtb+qngRen0SBEzLIuDxUVa90Nx9m9rNMp2TYj9aqqjrUbb8ArDpV5yQXAG8CvjXuwiZsXuNymloDPN9z+0DXNmefqjoKvAT87KJUNxmDjEmL5jsu1wH/0O9BPZ/9PCV5EPj5Oe76eO+NqqokJz2uNclq4O+AzVW17GctoxoXSYNL8gFgCnh3v76G/TxV1XtOdl+Sw0lWV9WhLsyPnKTfTwNfAT5eVQ+PqdRFNYpxOc0NcgqRY30OJHkD8DPA9xanvInwtCpzG2hckryH2cnUu6vq1X4P6jLOaO0ENnfbm4H7ju/QnT7iXuCOqrpnEWubpL7j0oBBTiHSO07vB/65Tu9PPXpalbn1HZck5wN/A/xeVQ02eaoqLyO6MLu+ugt4FngQOLtrn2L227oAPgD8H/BEz2XjpGuf9Lh0t/8FmAH+h9l1yksmXfuIx+EyZr/U51vM/lUH8MfdDyzATwJfBPYBjwK/OOmal8CY/Hr3WvhvZv/K2TPpmpfIuDwIHO7JkJ39HtPTJUhSA1zGkaQGGPaS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWpAf8PJxHm/X3mia4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plt.hist(values.mean(axis=1),bins=100);"
]
},
{
"cell_type": "code",
"execution_count": 68,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZQAAAEKCAYAAAA1qaOTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAABJB0lEQVR4nO29d5hkdZX//zpVXdU5p8l0z3QLDCJpmCEMihJNIEowY0BEZZVVf65+XVdXV3d118Wsq4iiqICggIowgChhYJghM0OYyOTOubtS1+f3x61bXdNT3V3h3qrq7vN6nvtM1a1bXZ++U33PPel9xBiDoiiKomSLJ98LUBRFUeYGalAURVEUR1CDoiiKojiCGhRFURTFEdSgKIqiKI5QlO8F5JOGhgbT0tKS72UoiqLMKp544oluY0zj5P3z2qC0tLSwadOmfC9DURRlViEiryTbryEvRVEUxRHUoCiKoiiOoAZFURRFcQQ1KIqiKIojqEFRFEVRHEENiqIoiuIIalAURVEUR1CDoigFxtaOIR7b0ZPvZSg55IlX+oiMR/O9jKxRg6IoBcZ37tvKv9z2bL6XoeSIPb2jvOPH67nzmf35XkrWqEFRlAKjdyRE70go38tQcsTevjEAXu4YzvNKskcNiqIUGP1jYYYCkTkRAlFmpms4CMDObjUoiqI4zMCo5Z0MjIXzvBIlF3QOBgDY1T2a55VkjxoURSkw+mOGpF8Nyrwg7qH0jBCNmjyvJjvUoChKARGMjDMaGgegf1QNynyga8gyKKFIlP0DY3leTXaoQVGUAiIxzNU/qon5+UDXUBCvR4DZH/ZSg6IoBcTgIQZFPZT5QNdQkGMWVQGzPzGvBkVRCohEI6I5lPlB51CQVy+uptTnZad6KIqiOEWiQRnQkNecJzwepXckRFNlMS0N5eqhKIriHIleiXooc5/uWIVXU2UJyxvK2dWjHoqiKA5hJ+Lryv30aQ5lzmNXeDVWFtPSUMbu3lHCs7ihVQ2KohQQA2NhPAJLa0u1ymse0DloeyjFtDZUMB417OmdvV6KGhRFKSD6R8NUl/qoLfdrp/w8wG5qbKwsprWhDIBdPSP5XFJWFJRBEZHzReQlEdkmIp9P8vprReRJEYmIyMWTXrtcRLbGtstzt2pFcY7+sTA1ZX5qSn1aNjwPsD2UhgrLQwHY0TV7DUpRvhdgIyJe4IfAOcBeYKOI3GmM2ZJw2G7gA8BnJ723DvgysAowwBOx9/blYu2K4hT9oyGqS33UlPnp05DXnKdrOEBtmQ9/kYdar4+qkiL1UBxiNbDNGLPDGBMCbgIuTDzAGLPLGPMsMDlrdR5wrzGmN2ZE7gXOz8WiFcVJBsbC1JT5qC71qeLwPKBzMEhTZQkAIkJrYwU7u9WgOMFiYE/C872xfW6/V1EKhv7RMDWlPmrLfAAMBiJ5XpHiJl3DQRori+PPW+vLZrX8SiEZlJwgIleKyCYR2dTV1ZXv5SjKIfSPhqwcSpk//lyZu1geSoJBaahgX/8YgfB4HleVOYVkUPYBSxOeL4ntc/S9xpifGmNWGWNWNTY2ZrRQRXGD8ahhKBihutRHdcxD0ebGuYsx5nAPpbEcgFdmaYNjIRmUjUC7iLSKiB94J3Bniu+9BzhXRGpFpBY4N7ZPUWYNQ4EwxkBNmY+a0phBUQ9lzjI4FiEUiU4KeVkGZbZKsBSMQTHGRICrsQzBC8AtxpjNIvJVEbkAQEROFpG9wCXA/4nI5th7e4GvYRmljcBXY/sUZdZglwlXl/qojYe81EOZq3QNW5MaEw1KS6wXZccsTcwXTNkwgDHmLuCuSfv+LeHxRqxwVrL3Xg9c7+oCFcVF7PBWTZmPGjvkpQZlzjLRJV8S31dZ4qOhophds9SgFIyHoijzHTu8VV3qp7LEh4jmUOYyiV3yiSxvKJ+1pcNqUBSlQBhI8FC8HqGqxKc5lDlM3EOpOtSgtDSUzdq5KGpQFKVAsMNbdkK+pkzlV+YyXcNBios8VBYfmnlobaigezjIUGD2/d+rQVGUAiExKQ9QU+bXkNccpnMwQFNVMSJyyP64SOQs9FLUoChKgdA/FqKyuIgir/VnWVPq06mNc5iu4SCNFcWH7Y+LRM7C0mE1KIpSIAyMhuMNjRALeamHMmdJ1PFK5Ij6MkSYlYl5NSiKUiD0x4QhbWpKffSNqIcyV5ncJW9T4vOyqLp0VpYOq0FRlAKhfzRETak//rymzM9gIMJ41ORxVYobBCPj9I+GD9HxSqR1lpYOq0FRlAJhYOzwkBfAoIa95hzdw5bnmcxDAbt0eARjZtfNhBoURSkQBsbC8ZJhmDAomkeZe3QOWrIrk3tQbFobKhgMROidZSFPNSiKUgAYY+Lz5G3s8Jc2N849uoZiXfIVhyflgVk7X14NiqIUACOhcSJRc0hSvlr1vOYsnUPJu+RtZut8eTUoilIA2F5IYlI+rjg8ph7KXKNrKIgI1Jf7k76+pLYUr0fUQ1EUJX3iXfKTyoYTX1PmDp1DQerL/fEm1sn4vB6W1ZXNukovNSiKUgDEhSETcihValDmLF1DQRqSdMkn0tpQriEvRVHSJy4MWTYRArEUh4s0KT8H6RoO0lSVPCFv01Jfzis9o0RnUR+SGhRFKQDsPEliUt56rgKRc5GuwUBSHa9EWhvLGQuP0zEUyNGqskcNiqIUAJOVhm1qVcJ+zmGMiXkoMxiU+Hz52RP2UoOiKAXAwFiYEp+HEp/3kP3V6qHMOfpHw4THTUoeCqhBURQlTSbreNmohP3cY6rRv5NZWFVCcZFnVolEqkFRlAJgYJLSsE1NmY8+DXnNKeKjf2cwKB6P0FI/u0Qi1aAoSgEwWXbFxlIcDqvi8Byia9hKss/koYAlErlDDYqiKOkwMDaFQSn1YQyzcr64kpy4hzJD2TBYEix7ekeJjEfdXpYjFKVykIiUAJ8CzgKamGSIjDGvcX5pijJ/6B8N85olyUNe9uuJPSrK7KVrKEipz0u53zvjscsbygmPG/b1j3FErOqrkEnJoAA/Ai4Cfg+sB9T/VhQH6R8LJTUYtkHpGw3RQuFfUJSZ6RyySoZFZMZjWxomKr3mkkF5G3CJMeY+F9eiKPOSQHicQDiaNORVbUvYa+nwnKFrKDhjybBNa4JBOfNIN1flDKnmUEaBPW4uRFHmK3EdryRVXrWxfQNa6TVn6BwKzNjUaNNQ4aeiuGjWlA6nalC+BXxaUvHRFEVJi7iOV7I+lDIdsjXXSMdDERFLJHKWGJRUQ17nAGcA54vIFuCQ2yVjzAVOL0xR5gvxWShJPJSqEutPVENec4NAeJzBQCSlCi+bloZynt7T5+KqnCNVg9IN/NHNhSjKfMU2FslyKEVeD5UlRa7qeXUOBagt8+ObYjaH4hwTo39T81DAyqP8+dn9BCPjFBfNXBmWT1IyKMaYD7q9EEWZrwyMTp1DAWtyo1shr2jUcO61D3LZqqV84U1Hu/IZygT26N/GFHMoYM2XNwZ294zS3lzp1tIcIa1bEhFZLiJvEZE3i8hytxalKPOJCen65H0mNWU+10JefaMh+kfD3LJpD8HIuCufoUyQmYdizZefDRIsKRkUEakSkd8D24DbgTuArSJyi4gUtslUlAJnYCxMkUembHSrLnVPwt6+Y+4bDXPflk5XPkOZoCs22yTVKi+YXTL2qXoo3wVeA7weKI1tZ8X2fceVlSnKPMHqgvdN2ehW42LIyzYoHoGbN2lngNt0DQXxCNSXp25Qqst81JX72dUzdwzKBcAVxph/GGPCse3vwJVYTY+KMmcZDkb42YM7XBNo7B8Lx+fHJ6Om1L2QV+egdcd84fGLeWhrF/v6x1z5HMWicyhIfUUxXk96HRizZb58qgalFOhJsr8XSL3+TVFmIes2H+Trd73Ac/sGXPn5A6NhaqYxKLVlPgbGwq7MFrc9lI+fuQJj4LYn9jr+GcoE6fSgJNJSXz6nPJRHgK+JSJm9Q0TKgX/H0vZSlDnLgQHrLr5j0J3Z3lPpeNlUl/ljisMRxz+7czBAZUkR7c2VnN5Wzy2b9rhiuBQLW8crXZY3ltMxGGQk6Px3wElSNSj/DJwC7BORf4jIP7CkWNYA17i0NkUpCA4MWGGgTrcMygweiv2aXQ3mJJ1Dwfigp0tXLWVv3xiP7kgWjFCcIBsPBQo/MZ+SQTHGPA+0A58DNsW2zwHtxpjNTi1GRM4XkZdEZJuIfD7J68UicnPs9Q0i0hLb3yIiYyLydGz7iVNrUpQD/ZYhscNDTjMwGqZ6ih4USFQcdj6PYhkUK2p93jELqCop4uaNmpx3g2jU0D2cmYdii0QWetgr1U55jDGjwM/cWoiIeIEfYsm87AU2isidxpgtCYd9GOgzxrSJyDuBbwKXxV7bbow53q31KfMXO+RlD0ZykvB4lKFgJKmOl42bel6dQwFOXFYLQInPy9tOWMxNG/fMaOSU9OkbDRGJmsw8lAYr27CzwBPzU3ooIvJ2EfElPJ5yc2gtq4FtxpgdxpgQcBNw4aRjLgRuiD2+FThLBSsVt7FDXh1Dzoe8BqdRGraxXxtwuNLLGEPnYPCQ2eaXrlpKKBLljmf2OfpZyoSHm46Ol02Zv4gFVSXsnMUeyq3AAqAz9ngqDOCEwMxiDpXI34uVo0l6jDEmIiIDQH3stVYReQoYBP7VGPNQsg8RkSuxyp1ZtmyZA8tW5jKB8Hg81OSGh9KfikGxcygOh7wGAxGCkSjNCRe4Vy+u5phFVdy8cQ/vP7XF0c+b78S75FOYJZ+M1oby2ZtDMcZ4jDGdCY+n2gpBrewAsMwYcwLwaeC3IlKV7EBjzE+NMauMMasaGxtzukhl9mGHu0p9XldyKLaRSCYMaWO/1udwyMvu2p58gbt01VI27x/keZfKpOcrcQ8lQ4PS0lBe8HNRCkledB+wNOH5kti+pMeISBFQDfQYY4LGmB4AY8wTwHbgVa6vWJnz2OGuYxdX0zMSJDIedfTnD8yg4wUxxeFi5xWHbY/LTsrbvO34xfiLPNyinfOOkq2HsryhnL7RcEHPxklVy+tSETk34fm/icheEblHRBY6tJaNQLuItIqIH3gncOekY+4ELo89vhj4mzHGiEhjLKlPTLSyHdjh0LqUeYxd4XXc0mqMge5hZ/+YJ4ZrTZ8Aryn3OZ5DmYjpH3qBqy7zcf4xC7j9qX0EwioY6RSdQwEqioso86dcC3UIifPlC5VUPZSv2A9E5ETg/wHfA3zAt51YiDEmAlwN3AO8ANxijNksIl8VEXuA18+BehHZhhXaskuLXws8KyJPY+V7rjLG9DqxLmV+czDWe/KaJTWAdVFwkunG/yZSU+q8npf9uyQLwVx28lIGAxHu2XzQ0c+cz3QNBTP2TuDQ+fKFSqqm8gjgpdjji4DbjTHfEpF1WAbAEYwxdwF3Tdr3bwmPA8AlSd53G3CbU+tQFJv9/WPUlvlYVmeVbXY4nJjvHw0jApUlMxgUFyTsOwaDlPq8VBQffhk4dXk9S2pLuWXTHi48frGjnztf6czSoCyrK8MjhW1QUvVQAoAtU38WcF/s8UDCfkWZcxwcCLCgujReCeWGh1JZXDSjWKAbEva2DEiyynuPR7jkpKU8sq2HPb2jjn7ufKU7S4PiL/KwpLZsThiUh4Bvi8iXgFVMeBGv4tBSX0WZU+wfCLCouoSGCj8izpcO949Or+Nl48bUxs7BwLQVRxevWoII/F6T846QKHOTKS0FXjqcqkG5GghhJcKvMsbsj+1/Iw6GvBSl0Dg4MMaC6hKKvB7qy/2Oeyj9Y+EZ8ydghbycVhzuSpBdScbimlLOaG/k1if2uibdP18YDUUYDkay8lDAqvTa1T2CMYX5/5GqltdeY8xbjTHHGWOuT9h/jTHmk+4tT1Hyx1jIampcWG1ddJsqS1zwUMLT9qDYVJf6iBoYclBtNpWY/mWrlrJ/IMDD27od+9z5SPeQ5V1OZ8BTobWhnJHQeLwEudBItWy4UUQaE54fKyL/ISLvcm9pipJf7AqvhdWlgFVe63Rz48BYOKWQl33MgEN5FPuOuXkGGZCzVzZRW+bjFhWMzIrOKZpI06XQS4dTDXndArwVQEQagAexqr1+IiKfcWltipJX7KbGCQ+l2PGZKP2joRl7UGCiT8WpbvmJpsbpL3DFRZZg5LotB+kdKdyGukIn3tSYgTBkIsvniEF5DfBY7PHFWCKOxwDvBz7qxsIUJd/YTY0LaywPpbmqhO7hoGP5hGjUxDyUmQ1Kbbk9E8UZD2WqpsZkXHbyUsLjhtufUsHITEnnfE/HoppS/F7PrDcopcBw7PHZTHSwP8mhcimKMmewQ14LqiY8lKiBnmFnwl5DwQhRM72Ol011qbMS9hNNjTPH9I9aUMVxS6q5ZdOegk0GFzpdQ0G8HqEuhfDmdHg9wrL6wi0dTtWgbAXeLiJLgXOBdbH9zUC/C+tSlLxjNzWW+i3906Z4L4ozBsXOh6SWQ3FWwj7VkJfNpScv5cWDQzy7VwUjM6FzKEBDhR/PDP1GqdBSX7ilw6kalH/HGma1C3jMGLMhtv884CkX1qUoecduarSxL75OlQ7bI31TyaHEFYdHnAt5+b2elMJtAG89bhElPg83a09KRmQru5LI8sZyXukdLchS7lTLhv8ALMNqajw/4aX7sDS1FGXOYTc12tgeilPyK6nqeAH4vB4qioscmyvfORigsTJ5l3wyqkp8vOnVC/nT0/sZC6lgZLp0ztDzkw4t9eWEIlH294858vOcJGX5emNMhzHmKaBRRDyxfRuMMS+6tjpFySN2U6ONXaHjVC9KXGk4RS+hpsznWNlwJrpSl568lKFghL8+f8CRNcwnuoaCWVd42RTyfPlU+1B8IvItERnCmknSEtv/TRH5uIvrU5S8YDc1LqqZCHn5izzUOdgtb1dsVaUQ8gJnBSI7h6aXXUnGmtY6WurLuFl7UtJiPGroHg5mXeFls7yxcEuHU/VQvozVh/JeIPH27HHgAw6vSVHyzuQKLxurF8WppLwVvkqlyguclbC3hSHTQUS4ZNVSNuzsLfjJgYVE70iIqMm+qdGmqbKYMr93VhuUd2FpeN0BJI6sex6djKhkwX/e9QL/8ectjk9CzJYDsfj0wppJBqWqJD46N1v6R8OU+b0UF6U2Rbu6zBnF4WBknP7RcEYx/XecuASPoNMc02C6uTOZICIFW+mVqkFZBLySZH8Rqc9UUZRDGAuNc/0jO7nu4Z1cdeMTBZXstWfJL0yo8gLrouBU2XD/WDilCi+bWodCXnbXdnMGIZgF1SWceWQTtz6xt+BuAgqVbEf/JqO1QFWHUzUom7GmIk7mUuAJ55ajzCc2vdJLeNxw4fGLuP/FTt5z3WMFMy97suyKTVNlMV1DQUdUf/tHw1Sn0ehmh7yy/ex413aGVUeXrlpK51CQB7d2ZbWO+UK25zsZrQ3l7O0bIxQpLKOeTh/K90Xki4AXuEREfoE1gvdrbi1Omdus395DkUf4xkXH8sN3n8jz+wa5+CePFkQ55IGBALVlPkp8h4ajmqtKiEQNvQ4YvoGx1HS8bGrKLMXh4VB2isN2lVqmd8xnHd1EQ4V/Tifn+0ZCDAWcKYBww0NpaShnPGrY01dYw89S7UP5E5Y3ci5WDuXLQDvwVmPMfdO9V1GmYv32Ho5fWkN5cRFvOnYhN3xoNR0DAd7+o/W83DGU17UdGAgcFu6ChOZGBxLz/aOp6XjZ2Mn7/iybG+0cUKZVRz6vh4tOWMz9L3QWrIx6trz7ug189vfPOPKzuoaCVJYUHXZzkg3x0uECC3vNaFDskmHgRWPM64wxFcaYMmPMWmPMupneryjJGAyEeW5vP6etqI/vO3VFPTd/9FSixnDxj9ezcVdv3tZnGZTDQxT2RbjDgcR8qsO1bGyJlmybGzuHgngE6sszv2O+ZNVSIlHD3ZsPZrWWQmR71zAvHBjkkW09juSJnOySt2ktUNXhGQ2KMSYMfBzIXoRGUWI8vqOXqIFTVzQcsn/loipu+9hpNFQU897rNrAuTxesAwNjh1V4wUQcvCtLD8UYw8BoOC76mAq1MeOTbaVX52CQhoriGefYT0d7UwWLa0p5eA7mUe7d0gHAcDDCCwey95Qz6fmZidoyH9WlvtlnUGLcA7zBzYUo84v123soLvJwwrKaw15bWlfG7686laMWVnHVjU/wu8d353RtYyGrrDZZyKvRIT2vsfA4ofFomh6KMxL2HUOBrJvsRIS1bQ2s395TkJpS2XDvlg4WxxpaN+zsyfrnWR6Kcwl5sM5/IVZ6pWpQ7ge+ISLfEZH3icjbEzc3F6jMTdZv72ZVS+2UceX6imJ+95E1nNHeyBf+8BzfvW9rzqTTp6rwAijxeaku9WXd3BjX8UojKW97MwNZFgR0DjqjK7W2vYGhQIRn9/Zn/bMKha6hIE/u7uOSVUtoqS9jw87sw66WjpezHgoUZulwqgblB0AT8EngBuDWhO337ixNmav0DAd58eAQp00Kd02mzF/EdZev4u0nLuba+17mS3c8n5O74YOxHpQFSQwKWP0b2Xoo6ep4QYLicLYhL4cucKe3Wf9/D2+dO/Pm//ZiB8bAOSubWd1ax8ZdvVmVaY8EI4yGxh3PoYBlUA4MBAqqfyvVKi/PNJtzpQvKvOCxHdZd36kJCfmp8Hk9fPuS4/jo65Zz42O7+cRvniQQdvcPaH/MoCxKEvICK4+SbXOjbVBS1fECS0usorgoqxxKZDxKz4gzBqWu3M8xi6p4eNvcMSjrNlvhrpULq1jTWk//aJiXsqg4nOhBccegADy3r3Bm1KSsNqwoTrF+ezcVxUW8ZnF1SseLCF9449F86S0ruXvzQS6//nHHBk0l42As5DWVh9JUWZx12fBAfBZKehP8qkt9WVV59YyEMGZCij9b1rY38OTuPkaC2fXGFAKjoQgPb+vmnJXNiAhrltcB8HgWYS83elBszjyykZoyHz98YJvjPztTUjYoIvI2EXlQRLpj20MicpGbi1MyZzgY4YGXOh3p6HaaR3f0sLq1jiJvevczH17bynffeTxP7u7jsv971DHV38nsHwhQV+6fMr9j6XkFs8rpZBLyso/PRsI+3UmNM3FGWyPhcZPVRbdQePDlboKRKOeubAZgSW0Zi2tKs0rMpzNqOV0qS3xc9boV/OPlrryW2CeSqnz9Z4CbgZeAz8W2F4Hfishn3VuekglPvNLLm777EB/8xcaCm7B3cCDAjq6RQ/pP0uHC4xdz/QdOZlvnMNc/vMvZxcU4OBA4TGU4kabKYkLj0axCT/1pDNdKpKbMR18WSfn4Bc4hD2VVSy3FRR4emgN5lHVbDlJd6uPk1rr4vjWtdTy+szfjmwc3PRSA9596BA0VxfzPPS/lrGhlOlK9RfwscLUx5iPGmOtj20ewkvSfcW95SjqEx6P877qXuOQnj2IwHLu4mv/664t0DxdON/OjO6wLTyr5k6k4o72RtqYK17rp9/ePsShJD4qNE82N/aNh/F4PpWl2T9eU+rMqG3Y6pl/i83JySx2PzPI8SmQ8yt9e7OQNRzXhS/CcV7fW0T0cYntXZtVUnUNBfF5Jq5ovHcr8RVz9+hVs2NnL+u3ZlzhnS6oGpQJ4IMn+B2KvKXlmZ/cIF//kUb73t228/cQl3PXJM7j2suMZDUX4+l9eyPfy4qzf1kNNmY+jF1Rl9XPamirY1jns0KoO5eBgYMr8CVh6XpCd/MrAWIjqMl/KI3htnAp5NTg0PRCsPMpLHUN0DroTgswFm17po380zDmxcJfNmuXWjU+mYa+uIauJ1JNFE+lMvGvNMhZVl/A/6/LvpaRqUG4HLk6y/x3AnY6tRkkbYwy/e3w3b/ruQ+zqHuFH7zmR/7nkOCpLfLQ1VXDV61bwx6f2FURppzGG9dt7OHV5fdZ/YO1NlezpG3W8ZHK6pkabuJ5XFpVe/aPpSdfb2FMbM71wdA5Z+SF/kXP1OGvt8uFZ7KWs29yBv8jDa1/VeMj+lvoymiqL2bAjsxyFWz0oiRQXefmns9p5anc/f3ux09XPmolUv1XbgM+LyD0i8pXYdjfwBeAlEfm0vbm3VGUyPcNBPvKrJ/jCH57jpCNqueea1/KmYxcecswnXt/GEfVlfOmO510vt52JPb1j7Osfyzh/kkhbUwXGWLpLTjJdU6ONnWDtyOKOPF1hSJuaUj/jUcNwhlVVHYPOX+BWLqyirtxfEDctmWCM4d4XDnL6inoqig8d7yQirM4ij+KGjlcyLj5pCUfUl/HtdS/ntRAnVYPyAaAPazrj5bHtyNi+DwL/FNuudn6JhcftT+3Le1XFAy92ct53HuLBrV186S0r+dWHVicN05T4vPzH217Nzu4RfvT37XlY6QTrt9v5k+kbGlOhvdmKtDptUA5OMVgrkVK/l8qSoqyUdvvH0tPxsqnOUs+rayjg+AXO4xFOW1HPw9u68x5yyYSXOobY0zvGOSsXJH19zfJ6Dg4G2N2bvlS8db6dr/CajM/r4Zqz29lyYDCvgp2pNja2prgtd3vB+SYUifLDB7Zx+fWP89iO3CfBxkLjfOn25/ngLzfSUOHnzqtP58NrW6cNIZ3R3sgFxy3iJ3/f7vgFOB3Wb++hqbKYFY3lWf+slvpyvB5ha4ezv8/+uEGZ/iJgzZbP3EMZGA1l5KHU2orDGRoUKwTj/AXujPYGOoeCbHUpr+Um6zZ3IAJnr2xK+vopsaqvdMNeVhNpKCceCsAFxy2mramC/7335bzpq6VaNjxlB5qIzHkjkoi/yMNvPrKGxTWlfOAXj+e0uuX5fQO85fsP8evHXuGKta3c/onTOSrF5Pa/vuVoSnwevvjH5/JyF2nnT05bUZ92IjoZ/iIPR9SXOZ6Yn6mp0aa5Krtu+YE0x//aTAhEpl86HI0auoaCWQtDJmNtu5V7mI3lw/du6eD4pTVTGtq2pgrqyv1p63rFm0hzZFC8HuHT57yKbZ3D3PH0vpx85mRSDXk9KyKHjQAWkQ8BTzu6ollAU2UJv7vyFFrqy/nQLzfy95fcTYSNRw0/+vs23vbDRxgJjvObK9bwr29ZmdbAnqbKEv7ljUfx2I5e/vBk7r9s2zqH6R4OzqjflQ7tTRVs7XS2dHimpkYba7Z8Zh5KKBJlJDSeYQ4l85BX32iISNTQ7MIFbnFNKcsbymednP2BgTGe2zdwWHVXIiLC6pa6tCu93O5BScb5xyxg5cIqvnPfVsIOzHJJl1QNym+B+0TkGyLiFZFaEbkN+A5wjVuLK2QaKor57UdOYUVjBVf+6gnuf6HDlc/Z2zfKu372GN+6+yXOO2YBd19zRlyUL13edfIyTlxWw9fveoG+kdzObrdr5LPpP5lMW1MFu3pGHZ2rPVNTo01TVQkdg5l1y9uyMdUZeCgTOZT0///iPSgONTVO5vS2Bjbs7C24OefTcV9s9sm5U+RPbNYsr2Nvn1VUkioTXfK5Mygej/DZ817F7t5Rbn1ib84+N/75qRxkjPkC1vjf9wKPA88CS4ATjTHXO7UYETlfRF4SkW0i8vkkrxeLyM2x1zeISEvCa1+I7X9JRM5zak3TUVfu57cfWcNRCyu56sYnuMfBZJgxhtuf2scbv/MQW/YP8j+XHMcP3n1CfGpfJng8wtcvOpaBsTD/9dcXHVtrKqzf3s3SulKW1pU59jPbmyoZjxpe6XFOwnumpkabpspiQpEog2PpV1vZOl7VGfxf2tpfmXgobgoVgtWPMhoa56ndfa78fDdYt6WD5Q3ltDVN3063utXW9UrdS8mHhwLw+iObOGFZDd+7f2vOKzvTKUZ/GPgrcALQDHzVGOOYKpmIeIEfAm8EVgLvEpGVkw77MNBnjGkDrgW+GXvvSuCdwDHA+cCPYj/PdWrK/Pz6w2s4ZlE1n/jNk/zl2QNZ/8yB0TCfvOlprrn5aY5cUMlfP3UGF5+0xJHcw9ELq7hibSs3b9qTM/2l8ajhsR29nLbcuXAXEL8IOJkInqmp0ca+y88k7BXX8crAQ/EXeSj3ezPqlrcbD91IyoPlfXpk9vSjDAbCPLajZ9pwl81RC6qoKilKKzFvGxQnm0hTQUT47LlHcmAgwE05Hk6XalL+VcAG4BzgTOBrwB9E5FoRyfyW+VBWA9uMMTuMMSHgJuDCScdciDWPBaxZLGeJdZW9ELjJGBM0xuzE6ptZ7dC6ZqS61MevP7ya45fW8MmbnsoqIbZ+ezfnf/dB/vrcAf6/847k5o+e6uhdPcCnzm5ncU0pX/zjczkJT7xwYJCBsTCntTkX7gJY0ViBCI4l5lNparSx7/IzGbSVqTCkTU2ZPzsPxYWkPEBViY/jltbMGoPy95e6CI8bzj1mZoPi9Uz0o6RK51CQ6lJfWrlOpzhtRT2nLK/jBw9sZzSUOyXoVD2Up4AXgOONMQ8aY74GvBZ4M7DJobUsBhKVDPfG9iU9xhgTAQaA+hTfC4CIXCkim0RkU1eXcwnEyhIfN3xoNauOqOWfb36a29KMXwYj43zjrhd4z3UbKPV5+cPHT+MTr2/Lau73VJT5i/jqhcewtXOYnz20w/GfP5l4/8lyZw1Kqd/LktpSxzyUVJoabZqz8VDi0xozuxerLvXFw2bp0DUUpLKkyNUL3BltDTyzp9/V8QJOsW7zQRoq/By/tDal41e31rGjeyRliZlcNTUmw/ZSuoeD/OrRV3L2uakalI8aY95rjBm0dxhjNgAnYuVUZg3GmJ8aY1YZY1Y1NjbO/IY0KC8u4pcfXM2pK+r57K3PcPPG1NzNlzuGeNsP1/PTB3fwnjXL+PMn1/KaJTWOrm0yZx3dzPnHLOB7929ld0/6DVvpsH57D21NFa4kg9saK9jqkEjkgRSaGm2ykV+xE+rVGXsovoymNnYOBVxPEK9tbyRq4NECECqcjlAkyj9e6uKso5pTvmlb02rreqXmpeRCdmU6VrXUceaRjfzkH9sZCuTGwKealL9xiv3DxpgrHFrLPmBpwvMlsX1JjxGRIqAa6EnxvTmh1O/l55efzBntjfzLbc9x42NT3x1Eo4ZfPLKTt3z/YToHA/z88lX8x9uOpcxfNOV7nOTLF6ykyCN86Y7nXetNCY9HeXxnryNyK8lob65kR/eII41cB1JsagTr5qHc782ouXFgLIxHoLI4s//nmjJfRlVeHQ7Nkp+OE5bVUO738vC2wi4ffmxHD0PBSErhLptjFlVR7vemHPbKp4di85lzjqR/NOzaqIfJTGtQROS3IlKZ8PyqSc9rReRBh9ayEWgXkdZYXuadHC48eSeW7AtYYpV/M9aV8E7gnbEqsFagnTx6TiU+Lz9930mcdVQT/3r78/zykZ2HHdMxGODyXzzOv/9pC2e0NXD3Na/lrKNT/3I7wcLqUj573pH84+Uu/vJc9sUEyXh2bz+joXHXDEpbYwWhSJQ9GchiTOZAf2pNjTaZNjf2j4apLvVlLJBZU+bPKKTUORRwLX9i4/N6WLO8nke2FbaHsm7LQUp93rRK8Iu8Hk5KsR/FGJMTj3Amjl1SzXnHNHPdQzsyuglJl5k8lMuARP//W0BinMgPnO7EQmI5kauBe7DyNbcYYzaLyFdF5ILYYT8H6kVkG/Bp4POx924GbgG2AHcDnzDG5FUJscTn5cfvPYlzVzbzlT9t4bqEXMXdzx/g/O88yMZdvXz9oldz3eWr8nYn8/5TWzh2cTX//qctDLrgFq/f1oPIRLjAadpiml5OJOYPDKbW1GjTWFlMVyZJ+bFwVuXfNaU++kfTUxw2xtDpgjBkMta2NbCze4S9fe6GUjPFGMN9Wzp57asa0s4nrWmt4+WOYXpn6OMaDkYIhKN591AAPn3OkQyHIvzfg+7nS2cyKJNvodwT9QeMMXcZY15ljFlhjPl6bN+/GWPujD0OGGMuMca0GWNWG2N2JLz367H3HWmM+aub60wVf5GHH77nRN587EL+4y8v8N37tvK5W5/hqhufZGldGX/55Bm8Z80RjpQDZ4rXI3zjomPpGQ7y33e/5PjPX7+9h5ULq6gtd6oY8FCcLB0+0D+WUrjLpqmqJKMhW/2joYyaGm1qynxEooaRNKT7BwMRgpGo6yEvsHS9gIJVH35u3wAHBwNTikFOxykpzpmf6Plx/3zPxJELKrnguEX88pFdWQmapoJzQxGUpPi8Hr77zuO54LhFXHvfy9z6xF7+6Q1t3Pax01jRWBizyY5dUs37T23hxg2v8PSefsd+biA8zhO7+1wLd4FVqtpcVeyIBMuBgUBaBqW5spjODLrlB8cyk663savD0lE76IqP/nX/jrmtqYLmqmIeKtDy4XWbO/AInHVUcjHI6Th2cQ0lPs+MYa98NTVOxafOaic0HuXHLiuOp2JQZp8edYFR5PVw7WXH869vPprfX3Uqnzn3yEPGjBYCnzn3VTRVFvP//vAcEYc0gJ58pY9QJOqoflcy2psq2e6EhzIQSKnCy6apqpix8Hjas0n6MxSGtLGNUTp5FHtSYy7umEWE09saWL+tO6+zOabi3i0dnNxSl5HX7C/ycOKy2hkbHN1WJUiX5Y0VvOPExdy44ZV4ebwbpHJV+08R+Z6IfA8rZ/LlhOdfd21lcwyvR7jijOWcdERdvpeSlMoSH1956zFsOTDIL9fvcuRnrt/eg9cjnNzq7u9sjwPOplJtNBRhYCycckIeEgdtpRdGsIZrZZFDyUDC3u2mxsmc0d5A32iYLQcGZz44h+zuGeWljqGUuuOnYk1rPS8cHJzWoBeahwLwybPaMcbw/b85JnByGDMZlAeBFcCxsW09sCzh+YrYMcoc4PxXL+ANRzXx7XUvs8OBuSnrt3dz3JLqw6bgOU1bUwUjofF42W8m2O9NRcfLxr44p9PcOB41DAbCVDngoaQjYZ9roUK7eqrQ5OzXbbH09mYSg5yO1a11GAObphmy1zkUwO/1ZJUrc5oltWW8a/Uybtm4x7Xes2kNijHmTGPM62faXFmZknNErAR9sc/DP/3uKYKRzAvlhoMRntk74Hq4CywZe8guMW9PalxQlUbIK+ahpJPoHAqEMSYzHS8b+73pNDd2DgYp9XldN+42TZUlHLWgsuD6UdZt6eCoBZUsq89czuiEZTX4vZ5pGxztHpR8Ftwkw1bf+O79W135+YUVyFfyzoLqEv774uPYvH+Qb/4186qvjTt7GY8aVxPyNvFKryw65vfHelAy8VDSaW7MVscLJjrsB9LoK+iMDdbK5QXu9LYGNu7qy7ni7VT0joTYtKs3q3AXWC0Bxy2tTsmgFBrNVSW8/9QjuP3pffGbKCdRg6Icxjkrm/nAaS1c/8jOjOe8rN/ebSUwj0hNJykb6iuKqSv3ZzXe2P7jak5DHqayuIhSnzee8E6FuI5XFgaluMhLmd+bZg4l9012a9sbCEWibJwmNJRL/vZiJ1GTXbjLZk1rPc/vG5iyIKNQDQrAx85s448fPy2tfGGqqEFRkvL5Nx7F0Qur+Ozvn8noTmb99h5OWlabM6VVS9Mrc4OyfyBAfRpNjWCFCJuqitPqlo/reGUoDGlTU+pLS8K+MweyK5NZ01qH3+spmH6UdZsPsrC6hFcvTm1s9nSsWV7HeNTw5CvJZ7/kW8drOurK/a5pBapBUZJS4vPyg3efQCAc5Zqbn0pLK6tvJMSWA4M5CXfZtDVXsDWLSq+DA2MZ3bE1VRanFfIacMBDAWs4V7pVXrm+Yy7zF3HiEYUhZx8Ij/PQ1m7OPrrZkbDfictq8XokaT9KeDxK70ioYD0UN1GDokzJisYK/v3CY3hsRy8/eiD1UsMNO3swBsfnn0xHe1MFA2Nhuocz0ytKtwfFpqmqJK2kfDbDtRKx5FdS+11HQxGGg5GclQwnsratgc37B+kZdrdDeyYe3trNWHg8LTHI6SgvLuLYxdVJ+1G6hwunSz7XqEFRpuWSk5ZwwXGL+M79W6ctk0xk/fYeyvxe1yX4E5mQYMksMZ9ul7xNU2W6Ia/M58knUlueesjLzvE05+ECt7bdkv57JM9y9uu2HKSyuMhRTbk1y+t4Zm//YUUHhdiDkiuyMigicp+IuNvLr+QVEeHrF72axTWlfOqmpxlIIcyyfnsPq1vrcqoG0N5kiWBn0jFvNzUuTKPCy6apsoThYISRFLvl+8dCVBYXUZTluakuTT3kleumxkSOXVxNVUkRD2/NX/nweNRw/wudnHlUE/4i576Ta1rrCI8bntx9aB5lQpVADUq6bEQbG+c8lSU+vv+uE+gYDPAvtz07bZ6iczDAts7hnOZPAJqriqkoLsqoFyWdOSjJPhdSH7Q1MBbOeLBWIjVl1tTGVHJGE02NufdQvB7htBUNPLy1Oyslg0B4nM37BzIaWf3U7j56RkKcm2W58GRWtdThEQ4Le3UNz18PJasuJ2PMF5xaiFLYHLe0hs+dfyTfuOtFfrNhN+895Yikxz26wwpt5KKhMRERiUuwpMvBNCY1TmZCfiVAa0P5jMcPjGYnDGlTU+ojPG4pDs/UrJjvO+a17Q3cvfkgO7tHWJ6BIOrevlGuuGETLx4coszvZU1rHWvbG1nb1sCrmitmTLKv29KBzyuceaSzE1qrSnysXFR1mPKwfb4bKtSgKMqUXLF2OQ9v6+Grf97CqpZajlpwePnl+m09VJf6OHph9qWZ6dLeVMHfX04/tGI3NebCQ7GEIbOX8o/Lr4yGZjYoQ0H8Xo8jhiwT4nL227rTNigbd/Vy1a+fIDQe5StvXcmO7hEe3trNAy9tASwvYG1bA2vbGji9reGwSj1jDPdu6eCU5fVUljj/+69uqec3G14hGBmnuMgqOe8aDlBb5nM0vDZbSMmgiMj1U7xkgACwDbjZGLPfqYUphYfHI3z7kuN443cf4urfPsWfrl5Lqf/Qvo31O7o5ZXldynO6naStqYLfP7GXgdH0wkqZNDXa2B5KZ4qlw/2jIRYkMcTpkigQuWSG3tHOoUBeZUCOqC9naV0pD23t5v2ntqT8vls27uGLtz/Hktoyrrt81SHjHvb1j/HI1m4e2tbNgy938cenrInf7U0VnB4zMKesqOfgwBg7u0f40NpWp38twErMX//ITp7dO8DJLZYIaj56fgqFVD2URuAMIAo8H9v3aqyBW08Abwe+KiJnGGOednqRSuHQWFnMtZcdx/t+/jhf/fNm/vPtr4m/tqd3lD29Y1yxdnle1tZuT2/sGkpL1TmTpkabqtIi/EWe3OdQSlOXsC+Eru21bQ38+ZkDRMajMxYkRMaj/OdfX+TnD+/kjPYGfvCuEw87Z4trSrn05KVcevJSolHDCwcHeWRbNw9t7eZ3j+/ml+t3UeSR+E3COS6N117dMjFwyzYoXcP5P9/5IlWf7BHgr8ASY8xrjTGvBZYAdwHrgCOAvwDfdmWVSkFxRnsjV71uBb97fA9/eXZiFv2j2+38SW4T8jZtjValV7od8wcHxjKq8AIrd9NcVZySh2KMsaTrHVCgTUfCvmMw/7PN17Y1MhQTDJ2OwUCYD9+wiZ8/vJMPnNbCLz5w8owG2OMRjllUzZWvXcGvP7yGZ758Lr/9yBqufO1y6iv8XHDcIldkRgBqy/0c2VzJYzsmyqJzNWq5EEnVQ/kU8AZjTFzz2BgzKiJfB+43xnxLRL4J3OfGIpXC4zPnvorHdvTw+T88y2uWVLO0roz127tpqCiO94TkmsW1pZT4PGkn5g8MBFhSm7n6bFNlSUoeykhonEjUOJOUL7MVh2dubuwcCrLa5Zk0M3HainpErAbDk6bQd9vZPcIVN2zklZ5RvnHRsbx7zbKMPqvE5+W0FQ2ctqKBz2Wz6BRZs7yOW5/YS3g8SpFH1ENJgQpgYZL9C2KvAQyiSf55g8/r4fvvOgEMfPKmpwiPR1m/vSd24chPrN7rEVY0VqRdOnxgIJCWyvBkUpVfsTvbnUjKV6cY8gpGxukfDec9pl9b7ufYxdU8MoUMy8Nbu3nbDx+hdyTEjVesydiY5IM1rfWMhsbZvH+QwbEIoUhUDcoM/BH4uYhcIiItse0S4OfAH2LHrAZedmORSmGytK6Mb7z9WJ7a3c81Nz1N51Awb+Eum3RLhzOZ1DiZ5qrUPJR4l7wDHkqJz0upzzuj/Irdtd2ch6bGyZze1sCTu/sOUeg1xvCrR3dx+S8eZ0FVCXdevZZTluf3O5QuJ7daHteGHT10DVs3FmpQpucq4B7gRmB7bLsRuBv4eOyYF4CPOL1ApbB563GLuGzVUv7ynJVLyXX/yWTamyrY1z+Wcud6fFJjBj0oNo2VxQwFIoyFpp/7EReGdGiKX02Zb8YcysRs8/xXHZ3R1kAkatgQyzeEx6N88fbn+bc7NvP6Ixu57eOnsbQu89BjvmiqLGF5YzmP7+xN6PnJ//nOBykZFGPMqDHmKqAOOCG21RljPmaMGYkd87RWeM1PvnzBStqaKjiivoyldZlfmJ3Azt+kOhvlQH9sUmMWHoqdgJ1pFPDEcK3sQ15ghb1mmtpoX+AK4Y75pJZaSnweHtraTe9IiPdet4HfbtjNx85cwf+9b1XOpkm6wZrWeh7f1cvBwfntoaTah3IN8FtjTCfwrKsrUmYdZf4ibr7yFEZD43kfedoW0/Ta1jmckjjlgYHYpMYsPBS7NLVzKMgR9VN3y9sz4J1qMLTlV6ajy5ZdKYCQV3GRl9Wt9dy7pYO/vdjJwcEA1152HBedsCTfS8uaNa11/O7x3TwUm/1SCOc7H6Qa8vo0sFdE7haR94jI7PNLFVepryguiHDFEfVl+LyScmLeDnllcwGw3zvT5EY75JWt0rBNbQozUTqHgngE6ssL4wK3tq2eff1jjIXHufnKU+aEMQHiVXTrNh+kuMhD5Sz2trIhVYNyBHAesAf4PtAhIjeKyPkiMv/0BZSCxef10FJfnnIvyoEsmhptEvW8pmNgNEyJz+PYFMuaspkl7DsHgzRUFOdFuSAZF5+0lI+c0cqdV5/OCcvcHw+dKxbVlLK0rpSR0HheVQnyTao5FGOMecAY8xGsUuHLgRKsCq+9Lq5PUdKmvbki9RxKFk2NNrVlPnxembHSy2pqdCZ/ApaE/cBoeHr156FAQYVf6sr9fPHNKzMS4ix07Fkr87WpETKQrzfGhIBHY9srWAZGUQqGtsYKXukZOWzwUTIODgRYUJXdxU1EYs2NMyTlx0KOhbvA8lBC41FGp6kus2abz8+Ko1yzJhb2mq8JeUjDoIhIpYh8UETuA3YDVwC/BVa4tThFyYS25kqiBnb1jMx47P7+sayaGm0aK4tnzKH0pylaORO1tuLwNGGvjnksA5JrJjyU+WvAUzIoInIr0AH8J7AZOM0Yc7Qx5mvGmJ1uLlBR0qXdHgc8Qx5lJBhhMBBxROepuap4Rg9lYMwZHS+b6lJbzyt5pVdkPErPiBqUXLG0rpT3rFnGecfM36BNqqUIQeAdwDpjzCH+tYicbYxRDS+lYGhtKMcjzFjp5URTo01TZQkbJg1amkz/aJjXLHE25AVMOZa5ZySEMdCUgSy/kj7WuOxj872MvJKSQTHGvCfxuYgsBj4IfAirAsyZshVFcYASn5dldWUzzpe356A44aE0VRbTPxomEB6fsoqrfyzkWFMjJApEJjco+Z7UqMw/0smheEXk7SJyF7ALuAj4CdDm0toUJWPamirY2jk07TH7HWhqtLGbG7umqPQKhMcJhKPOJuXtkNcUzY3xWfLqoSg5YkaDIiJHish/A/uB/wGejL30PmPMtzSHohQibU2V7OweITIenfKY+KTG6uzv4BtnGAUc1/FyMCk/MQZ4Cg9lSD0UJbdMa1BE5CHgMaAWuNQYs9wY8685WZmiZEF7UwXhccMrvaNTHnNgIEBDhT8+Czwb4npeUzQ3xnW8HOxDKfF5KfF5ppSwt0NeDRVqUJTcMJOHcirwK+BaY8w/crAeRXGEthQqvQ4MjDk2yS9RzysZ8VkoDnooYBmoqaq8OocC1JX78RepmIWSG2b6pp2Mlbh/WESeEpF/FpH5WxOnzBpWpKA6fHAg4FjHdl2ZnyKPTFk67LSOl01N2dSKw1ZTo3onSu6Y1qAYY54yxnwCa1rj/wIXYOl5eYA3i4gjYjwiUici94rI1ti/SX+uiFweO2ariFyesP/vIvKSiDwd25qcWJcye6koLmJRdQlbO6ZOzO/vH2OhQx6KxyM0VBTTMUVzY78LORSwDNRUZcOdQ/N3FK2SH1LV8goYY35tjHk9cDTw38A/AwdF5K8OrOPzWLPp24H7Y88PQUTqgC8Da7CmQ355kuF5jzHm+NjW6cCalFlOW3Ml26bwUOymRic1pazmximS8g7PQrGpLfNPWeXVNRiY113bSu7JRMtrmzHm88BS4FJg+oEMqXEhcEPs8Q3A25Iccx5wrzGm1xjTB9wLnO/AZytzlPbYOOBo9HDxRLup0SkPBaCxsmTqpPxYCK9HKPc727I11dTGaNRYIa8CEoZU5j4ZZ+uMMePGmDuMMRc6sI5mY8yB2OODQHOSYxZjhdts9sb22fwiFu76kkyjHS0iV4rIJhHZ1NXVlfXClcKlramCQDjKvv6xw1476IJBmc5DsZSGfY7LmlfHJOwnKw73jYaIRI3mUJSckrPyDxG5T0SeT7IdYpCM9ZcxtR53ct5jjDkWOCO2vW+qA40xPzXGrDLGrGpsbEz791BmD7am17YkHfN2U6OTIa+myhJ6R0KEIof3vvSPOSsMaVNT6icUiTI2SVnZNmzN2tSo5JCcGRRjzNnGmFcn2e7AGti1ECD2b7IcyD6sMJvNktg+jDH2v0NYCsir3fxdlNlBvHQ4Sce8k02NNnZ4qWv4cC9lYNRZYUib2imaG7WpUckHhVKgfifW0C5i/96R5Jh7gHNFpDaWjD8XuEdEikSkAUBEfMBbgOdzsGalwKkp89NQUZzUQzkwMOZYU6NNc9XUzY1O63jZTNUtb69Bk/JKLikUg/JfwDkishU4O/YcEVklItcBGGN6ga8BG2PbV2P7irEMy7PA01hey89y/hsoBUlbU3lS1eEDDvag2NgX72R5lH6XPJTqKfS84h6KJuWVHJKqfL2rGGN6gLOS7N+ENcjLfn49cP2kY0aAk9xeozI7aW+q5Pan9mGMOSQhfqA/wLL6Mkc/azr5lQGHh2vZTOWhdA0FqSwpcmx+vaKkQqF4KIriCu3NFQwFI4d5DQcGxljkYIUXQH1FMR453EMJj0cZCkYc1fGymTLkNRTQ/ImSc9SgKHOatsbDNb0mJjU6G/LyxrrlJ48CHnSpSx6sxkZIEvIa1FnySu5Rg6LMadqa7dLhiUqv+KRGB2bJT6apqpiOSXpebkjX25T4vBQXeQ6TX9GmRiUfqEFR5jSNFcVUlRQdkpg/EOtBWeBCj0ZzZclhHkq/S8KQNpO75Y0xdAxqyEvJPWpQlDmNiNDeXDnJoNgeirMhL7A8lMk5FLd0vGxqSv30JUjYDwYiBCNRDXkpOUcNijLnaW+qOGS+/IF+ezSu83fwjZUl9IwED5kUaec33CgbhpiHkjBkq2vIvd9PUaZDDYoy52lrqqBnJETviHVhPzg4RkNFsaNNjTbNVcUYA93DEx6DHY5yM+SVmEOxQ27qoSi5Rg2KMudpm6Tptb8/4KgoZCITzY0TiXnboFS5ZVBKD5Ww16ZGJV+oQVHmPJM1vaxJjW4ZFOsinjhoa2AsTFVJEV6Ps0rDNvbURltx2DZmmpRXco0aFGXOs6i6lDK/N96Lsn/AuUmNk5mYLZ/oobij42VTXeYjFIkSCFt5m87BIKU+LxXFBSGEocwj1KAocx6PR2hrqmB71zDDwQhDgQgLXajwAmio8CPCIaXD/WNhV3pQbCY3N9o9KE7PXlGUmVCDoswL2hor2NoxzMH4HBR3PJQir4f6cv9hORS3EvIwUT1m52pUdkXJF2pQlHlBW3MFBwcD8bCXG02NNk2TmhsHxsKuh7wg0aCo7IqSH9SgKPMCW9ProW3dgDtNjTaTmxv7R0Ou9aAAcdHJ/lhzY9dgkEb1UJQ8oAZFmRe0N1cC8ODLXYC7JbVNlcV0xCTso1ET81BczKGUxzyUsTCjoQhDwYiWDCt5QctAlHnB0tpS/EUe9va519Ro01xVQvdwkPGoYSQUIWrca2qERA8lHA+1NWvIS8kD6qEo84Iir4flDeWAewl5m6bKYqIGekaCrut4AZT4PPiLPPSPhbSpUckralCUeYPd4Oi2QWm0u+UHg/FEuZs5FBGhptRH/0g4oalRPRQl92jIS5k35MqgNMe8g86hAD6vdc/mxvjfRCyByFCCjpd6KEruUYOizBvam6zEvFtNjTZNsZLkjsFgvFvdTQ8FrJBa/2iYzqEgfq/H1SIARZkKDXkp84ZjFlUhQjyX4haNFTEPZTA4MVzLbQ+l1MfAmBXyaqzULnklP6iHoswbWhrKuf/Tr6Ol3l2D4i/yUBfrlo9FvFyt8gIr5PXs3jBdQ9qDouQPNSjKvGJ5rMHRbaxeFEuksczvdbVMGayQV9+olUM5or7M1c9SlKnQkJeiuEBTVQldQwFLGNJl7wQsDyUYibKnb1RLhpW8oQZFUVygqdKSX+kfDVPtYg+Kjd3cOBoa15JhJW+oQVEUF2iqLKZrKEifyzpeNolVXVoyrOQLNSiK4gLNVSVEooZd3SM5KeFNNFrNLiopK8p0qEFRFBewvYSekVBODEpiWbJWeSn5Qg2KorhAYmK8utT9HEptQp5Gk/JKvlCDoigukJgYz0nIK/YZHoH6cjUoSn7QPhRFcYHEsJPbTY0ApT5vXHLF69EueSU/qIeiKC5Q4vPGDUkuqrxEhOoyn4a7lLyiBkVRXMJWHXZbx8umsaKYRdXuCl8qynRoyEtRXKKpsoSXO4bjTYduc+1lx1Pmd1fiRVGmQw2KoriEXTqcKyn5IxdU5uRzFGUqNOSlKC5hz0XJRVJeUQoB9VAUxSXeceJiqkt9lBfrn5kyPygID0VE6kTkXhHZGvu3dorj7haRfhH586T9rSKyQUS2icjNIpKboLWiTEN7cyUfO3NFvpehKDmjIAwK8HngfmNMO3B/7Hky/ht4X5L93wSuNca0AX3Ah11ZpaIoijIlhWJQLgRuiD2+AXhbsoOMMfcDQ4n7xJp1+gbg1pneryiKorhHoRiUZmPMgdjjg0BzGu+tB/qNMZHY873A4qkOFpErRWSTiGzq6urKbLWKoijKYeQsWygi9wELkrz0xcQnxhgjIsatdRhjfgr8FGDVqlWufY6iKMp8I2cGxRhz9lSviUiHiCw0xhwQkYVAZxo/ugeoEZGimJeyBNiX5XIVRVGUNCmUkNedwOWxx5cDd6T6RmOMAR4ALs7k/YqiKIozFIpB+S/gHBHZCpwde46IrBKR6+yDROQh4PfAWSKyV0TOi730L8CnRWQbVk7l5zldvaIoilIYjY3GmB7grCT7NwFXJDw/Y4r37wBWu7ZARVEUZUbEihjNT0SkC3glxx/bAHTn+DMLHT0nh6Pn5HD0nBxOvs7JEcaYxsk757VByQcisskYsyrf6ygk9Jwcjp6Tw9FzcjiFdk4KJYeiKIqizHLUoCiKoiiOoAYl9/w03wsoQPScHI6ek8PRc3I4BXVONIeiKIqiOIJ6KIqiKIojqEFRFEVRHEENiouIyC4ReU5EnhaRTbF9KQ0Tm0uIyPUi0ikizyfsS3oexOJ7sWFpz4rIiflbuXtMcU6+IiL7Yt+Xp0XkTQmvfSF2Tl5KUIiYU4jIUhF5QES2iMhmEflUbP+8/a5Mc04K8ruiBsV9Xm+MOT6hVjzVYWJziV8C50/aN9V5eCPQHtuuBH6cozXmml9y+DkBa1Dc8bHtLgARWQm8Ezgm9p4fiYg3ZyvNHRHgM8aYlcApwCdiv/t8/q5MdU6gAL8ralByT0rDxOYSxpgHgd5Ju6c6DxcCvzIWj2EpSS/MyUJzyBTnZCouBG4yxgSNMTuBbcxBqSFjzAFjzJOxx0PAC1izjebtd2WaczIVef2uqEFxFwOsE5EnROTK2L5shonNJaY6D4uBPQnHTTswbQ5ydSx8c31COHTenRMRaQFOADag3xXgsHMCBfhdUYPiLmuNMSdiueafEJHXJr4Yk96f93Xbeh7i/BhYARwPHAC+ndfV5AkRqQBuA64xxgwmvjZfvytJzklBflfUoLiIMWZf7N9O4I9YrmeH7ZZnMExsLjHVedgHLE04bt4MTDPGdBhjxo0xUeBnTIQq5s05EREf1oXzN8aYP8R2z+vvSrJzUqjfFTUoLiEi5SJSaT8GzgWeJ4thYnOMqc7DncD7YxU8pwADCeGOOc2k+P9FWN8XsM7JO0WkWERasZLQj+d6fW4jIoI1y+gFY8z/Jrw0b78rU52Tgv2uGGN0c2EDlgPPxLbNwBdj++uxKlW2AvcBdfleaw7Oxe+w3PIwVkz3w1OdB0CAHwLbgeeAVflefw7Pya9jv/OzWBeGhQnHfzF2Tl4C3pjv9bt0TtZihbOeBZ6ObW+az9+Vac5JQX5XVHpFURRFcQQNeSmKoiiOoAZFURRFcQQ1KIqiKIojqEFRFEVRHEENiqIoiuIIalAUJQ+IyAdEZDjf61AUJ9GyYUVxGBGZ6Y/qBuBjQKWxVBQUZU5QlO8FKMocJLGL+S1Y0hiJ+8aMMWPAWE5XpSguoyEvRXEYY8xBewP6J+8zxgxMDnnFBiY9LyKXizWYbUREfiEifhH5uIjsEZEeEflfEfEkvM8vIt8Ukb0iMioiG+fqAC6l8FEPRVEKhxaseRZvwZIcvw3LszmApQV3FHAL8EjsNYBfYKnOvhtLwuVNwJ9E5GRjzDO5XLyiqEFRlMLBC3zQGDMAPC8idwOvAxYbY0LACyLyCPB64DYRWQG8C2gxxuyO/YwfiMjZwEeBj+f+V1DmM2pQFKVw2B0zJjYdwMsxY5K4ryn2+EQsgcQtlihtnGLgb24uVFGSoQZFUQqH8KTnZop99oxwT+z5yUmO04S/knPUoCjK7OUpLA9lgTHmgXwvRlHUoCjKLMUY87KI/Ab4pYh8BngSqAPOBHaYiYmHipIT1KAoyuzmg1gDlb6FNe61F2tCn3osSs7RTnlFURTFEbSxUVEURXEENSiKoiiKI6hBURRFURxBDYqiKIriCGpQFEVRFEdQg6IoiqI4ghoURVEUxRHUoCiKoiiO8P8D9MDKwcuORUwAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plt.plot(header,values.mean(axis=0))\n",
"plt.xlabel(\"Time\",size=14)\n",
"plt.ylabel(\"Avg. Expression\",size=14);"
]
},
{
"cell_type": "code",
"execution_count": 69,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 69,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAY4AAAEKCAYAAAAFJbKyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAABhBElEQVR4nO2deXhU1dnAf2eyb2RPgIRsEPadgCCgqKhgVdxw36vWqv3aqm1dqrW2ttZaa21xrVZxR1xARUUBRWQz7EtWIIQQyL7vyZzvjzMTkjBJZjIzmZlwfs8zz8zce+feNzcz973vLqSUaDQajUZjLQZXC6DRaDQaz0IrDo1Go9HYhFYcGo1Go7EJrTg0Go1GYxNacWg0Go3GJrxdLYCziYqKkklJSa4WQ6PRaDyKbdu2lUopoy2tG/CKIykpifT0dFeLodFoNB6FEOJwd+u0q0qj0Wg0NqEVh0aj0WhsQisOjUaj0diEVhwajUajsQmtODQajUZjE1pxaDQajcYmtOLQaDQajU1oxdENRqPkL6syOFJe72pRNBqNxq3QiqMb8srqeG9rPouW/MCPeeWuFkej0WjcBq04uiElOphP7p5NaIAP176ymQ/Sj7haJI1Go3EL3EpxCCEWCCGyhBC5QogHLKy/UwixRwixUwixQQgx1pnypEQH88lds5mRHMFvlu/mr6syaDPqiYkajebUxm0UhxDCC1gCLATGAtdYUAzvSCknSCknA08BzzhbrtBAH16/ZQbXz0zgpfUH+dmb6dQ2tTr7sBqNZqBhbIPSHFdL4RDcRnEAM4BcKeVBKWUz8B6wqOMGUsrqDm+DgH65/ffxMvDnSybw+KJxrMsq4YoXNuqguUajsY3d78OS06C60NWS2I07KY44oGMgocC0rBNCiLuFEAdQFsf/WdqREOIOIUS6ECK9pKTEYQLeOCuJ12+ZztHKBi5Z8gPpOmiu0Wis5dgukG1QvN/VktiNOykOq5BSLpFSDgd+B/y+m21ellKmSSnToqMttpPvM3NTo/n4rtmE+Htz7StbWL6twKH712g0A5SSTPVcdsC1cjgAd1IcR4FhHd7Hm5Z1x3vAJc4UqDtGxKiMq2mJ4dz/wS6e/CITow6aazSanijJVs8DIM7hTorjRyBVCJEshPAFrgZWdtxACJHa4e1PAJf9B8ICfVn60xlce1oCL353gJ+9tY06HTTXaDSWaKyCGlNsoyzXtbI4ALdRHFLKVuAe4CsgA1gmpdwnhHhcCHGxabN7hBD7hBA7gXuBm1wjrcLHy8ATl4znsYvGsiajiMtf2EhBhQ6aazSaLpitDf/QAaE43Gp0rJRyFbCqy7JHO7z+Zb8L1QtCCG6enUxydDD3vLOdS5b8wEs3pDEtMdzVomk0GnehNEs9j1ygsqtaGsAnwLUy2YHbWByezpkjVdA8yM+ba17ezP7C6t4/pNFoTg1KMsHLF0bMV+89PECuFYcDGRETzEc/Px1fbwMvrffsL4ZGo3EgJdkQmQrRo9R7D3dXacXhYCKD/bh6+jA+232Mo5UNrhZHo9G4AyWZSmlEjlDvyzw7s0orDidwy5xkAF7/4ZCLJdFoNC6nuR4q85Xi8A2CQXHaVaU5mbiwAH4yYQjvbj1CdWOLq8XRaDSupCwHkCfcVJHDPb6WQysOJ3H73BRqm1p5f6tux67RnNKYU3GjzIojVSkT6blFw1pxOIkJ8aGclhzB/344REub0dXiaDQaV1GSCcJLWRqg4hyNVVBf5lq57EArDidyxxkpFFY1smrPMVeLotFoXEVpFkQkg7efeh9laoDhwZlVWnE4kbNGxZASHcQr3x9EerBZqtFo7KAkC6JHn3hvtjw8OM6hFYcTMRgEt89NYe/RajYf1C3YNZpTjtZmKD8IUSNPLAtLBIOPtjg03XPplDgig3x55fuDrhZFo9H0N+UHwdja2eIweEFEilYcmu7x9/HihlmJrM0sJre4xtXiaDSa/sTcoyp6ZOflUalacWh65oaZifh5G/jv97ogUKNxK+pKwejErMcSk+KI6qI4IoebrJE25x3biWjF0Q9EBvtx+bR4PtpxlJKaJleLo9FoAOrL4dmJsP115x2jJAtCE1TFeEciU6GtGSoPO+/YTkQrjn7ip3OSaW418uZmz/yiaDQDjoIfoaUODn3vvGOUZJ2oGO9Ie88qz2w9ohVHPzE8Opj5Y2J5c1MeDc2eaZ5qNAOK/M3q+Wi6c/ZvbFMV4pYUh7mWw0NTcrXi6Edun5tMRX0LH24vcLUoGo3myFb1XJkPtSWO33/lYWhttKw4AiM9ehqgVhz9yIzkCCbFh/LqhkMYjbogUKNxGW0tcHQbDJ6o3hdud/wxuvao6ogQJ3pWeSBacfQjQghum5vCodI6vskocrU4Gs2py/Hd0NoAp92p+kgVOMFdVZKpnrum4pqJHKFjHBrrWDh+MHFhATo1V6NxJflb1HPKPIgZq6wPR1OSBcGDISDc8vqoEVB9FJrrHH9sJ+NWikMIsUAIkSWEyBVCPGBh/b1CiP1CiN1CiDVCiERXyGkP3l4Gbp2TzNa8cnYeqXS1OBrNqcmRLRA6DELjIG6qUhyO7idXmtW9tQHKVQUeaXW4jeIQQngBS4CFwFjgGiHE2C6b7QDSpJQTgeXAU/0rpWO4avowQvy9dRsSjcYVSKkUx7DT1Pu4adBYqQryHHmMkuzOrUa64sFjZN1GcQAzgFwp5UEpZTPwHrCo4wZSynVSynrT281AfD/L6BCC/by5dkYCX+w5xpHy+t4/oNFoHEfVEag5dkJxxKepZ0e6q6oLobnm5Irxjpi75GqLwy7igI7j8gpMy7rjp8AXTpXIidw8OwmDELym55JrNP2LOQ03waQ4okeDT5BjFUd7YLwHi8MnQLnLPLCWw50Uh9UIIa4H0oC/d7P+DiFEuhAivaTECfnZDmBIaAAXTRrKsh+PUNWg55JrNP1G/malKGLGqfcGLxg62bGZVaWmVFxLNRwdiRzhkbUc7qQ4jgLDOryPNy3rhBBiPvAwcLGU0mLjJynly1LKNCllWnR0tFOEdQS3zU2mrrmNd7fmu1oUjebU4cgWiJ8GXt4nlsVNNaXoNjvmGCWZKpsqqJfrj1lxeNigN3dSHD8CqUKIZCGEL3A1sLLjBkKIKcBLKKVR7AIZHcq4oaHMHhHJ/344RHOrnkuu0Tidphoo2gvDZnZeHpemmg4W7XXMcUqyVeGfED1vF5UKTdVQ556eke5wG8UhpWwF7gG+AjKAZVLKfUKIx4UQF5s2+zsQDHwghNgphFjZze48htvmplBU3cRnuwtdLYpGM/A5ug2k8URg3EzctBPrHUFJZu9uKvDYMbLevW/Sf0gpVwGruix7tMPr+f0ulJOZNzKa1JhgXl5/kEunxCF6u0PRaDR9J38LIE5kUpkJjYegGJPiuN2+Y9SVQkO5lYrDXMuRC0mz7TtuP+I2FsepihBqLnnm8Rp+yC1ztTgazcDmyBaIGQMBYZ2XC5MycYTF0Z5RZYXiCI0HLz+Pq+XQisMNWDRlKFHBfrogUKNxJkajmsHR1U1lJm6qyoZqqLTvOO1T/6xQHAYv5a7ysFoOrTjcAD9vL24+PZHvskvIOq7nkms0TqEkQwWiu1UcpjhH4Q47j5MFvsHKmrCGyOEeF+PQisNNuO60RPx9DPxXWx0ajXM4YmpsmNCN4hg6VT3b664qzVLZUtbGKyNToeKQavXuIWjF4SaEB/lyZdowVuwspLi60dXiaPqB+5btYln6kd431DiG/C2qriI82fL6gDB1EbdXcZRk9Vwx3pXIEWBsVQOlPAStONyIW2cn02I08samPFeLonEyjS1tfLyjgC/3Hne1KKcO5saGPVkCcdNUBXlfC/Iaq1QfrJ56VHXFA8fIWqU4hBD+QojfCSFWm+ondnd8OFvIU4WkqCDOGxvLW5vzqW9udbU4GidysKQOo4S8Us+bxeCR1BYrd1B38Q0z8WlQV6zmZPQF89Q/Wy0O8KjWI9ZaHM8DDwB5wCfAh10eGgdxxxkpVDW08EG6nks+kMkpVkkQ+eX1tLbprgFOpz2+MbPn7eLsjHOUmjKqrEnFNRMYAQERHpWSa20B4CXAYinlN06URQNMS4xgSkIYr244xPUzE/Ey6ILAgUhucS0ArUbJ0coGEiODXCxRN2R8Bp/9Gu7eoi5wnkr+ZlUvMWRSz9vFjgcvX+WuGruo520tUZKpjhNm44y5qFSPSsm11uKop3PLc40TuWNuCvnl9Xy9X/u/Byo5RbXtrvZD7uyu2vhv5brJ3+RqSezjyFYYOgW8/XreztsPBk+Eo9v7dpySbKUEvGxsyhE5YuDFOFCT9u4Vuh9Gv3DeuMEkRATy8nqdmjtQySmuYfKwMMCN4xwlWXBks3rtyYqjpRGO7YRhM6zbPm6aquUwttl+rJJM2wLjZiJHQO1x1YTRA7BWcZwLXAXkCSG+EEKs7PhwonynJF4Gwa2zk9ieX8m2w+WuFkfjYJpbjeSV1XP68EiCfL3IK3PTKZDbl4LBR1VA5292tTR959hO1fm2t8C4mbhp0FJ3onWItTTXq5RaWwLjZjwsQG6t4igFPgbWAseBsi4PjYNZnDaM0AAfXlmvJwQONPLK6mgzSkbGhpAYGURemRtaHK1NsPMdGH0BjFoIhTvVhdETMQfGbVEcYHuAvCwHkBDdB4vDnJLrIXEOqxxxUspbnC2IpjNBft5cd1oCL3x3gMNlde4bPNXYTE6RCoyPiAkmOSqIfYVVLpbIApmfqQ6vU29SFc0/PAuF2yFpjqsls538LRCRAsFWDnWLHA7+oUpxTL3R+uOYe1T1xeIITwaEx8Q5bCoAFEKkCCEuFEL8RAiR4iyhNIqbT0/C2yB4bYO2OgYSOcU1CAHDo4NJigrkSEUDLe6Wkrt9KYQmQMpZJ2IDnhjnkNJU+NdLGm5HhDAVAtpocZRkgfCCiOG2fQ7Axx/CEgaWq0oIMUgI8QGQi6rjWAHkCCGWCSFCnCjfKU3MIH8WTY5jWXoBlfUOGmmpcTk5xbUkRATi7+NFUmQQbUZJQUWDq8U6QfkhOPgtTL0BDAaVhhs9Bg57oOIoPwj1pdYHxs3ETYPi/dBsgxuxJFNZNt6+th3LTOQIj6nlsNbi+BcwETgLCDA9zjEte9YpkmkAuH1uCg0tbby9xXP62Gh6JreoltSYYACSo5QL0q0yq3a8CcIAk687sSxxlkpp7UumkSuxtvCvK3FpINvgmA2NMUqzbSv864q5lsMD5o9bqzguBm6TUn4npWwxPb4F7kAVB2qcxKjBIZwxMprXN+bR1OphP1ozTTXw3BTY+5GrJXE5LW1GDpbWMiJGGerm2JXb1HK0tcKOtyH1PAiNO7E8YRY010DRPtfJ1hfyN6t4hTWzMTrSXkGebt32rc3qom+P4ogcAc21UOP+9VvWKo4ALGdPlQP+jhNHY4nb5yZTUtPEip0eOpf8wFrlMvjmD+oHdgpzuKyeljbZbnFEBfsS7OftPplVOatVPUHXoLD5jt3T0nKPbIX4GcrlZgvBMSrGY21mVflBZaHYqqA64kEpudaezR+APwkhAs0LhBBBwB+Bjc4QTHOCOSOiGD04hP9+fxDpAWbsSWSvVkHDynzY9Y6rpXEpuaYeVSNjlcUhhCApKtB9LI7tb0DwYEg9v/Py0GEwKM6zAuQNFWp4k7VpuF2Jn2a94rBlXGx3tCsO949zWKs4fg3MBI4KIb4TQnyHakFyGvArJ8mmMWGeS55dVMt32SWuFsc2jEbI+Ur1/YlLg/VPu63VsTG3lGe/yXbqMcypuMNjTqRXJ7lLLUfVUWVxTLnu5JYZQiirI3+Tc33wXz4EH97mmGMUmNxM3Q1u6o24aepmp9aK31yp6XtjrsfoC4PiwDvAI2o5rFIcUsq9QCrwWyDd9PgtkCqldJjTUwixQAiRJYTIFUI8YGH9GUKI7UKIViHEFY46ridw0aShxA7y47/fe1hq7rEdUFcCI8+Hsx6EqiMq+OqGvPvjEf61JofaJue1tM8priU+PIBA3xMX5uSoII5WNNDc6uKU3J1vgzTClBssr0+YpWZNOGvgUGuzsnj2fAA5X9u/vyNblKVrLuizFVsKAUsyVTqtrx31VgaDx4yRtdrxJ6Wsl1K+IqW8z/T4r5TSYTmEQggvYAmwEBgLXCOEGNtls3zgZuCU83f4ehu4+fRkNuSWumfBWHdkrwYEjDgXhp+j/M3f/0NVJrsZh0prkRL2HnXe+c0pPpFRZSYpMgijVC3WXYbRCNvfhOQzIaKbCXnOjnMc/kEFh739YfXD9o9Szd8Mgyf0/WI+ZJJSPFYpjmz74htmPCQlt1vFIYS4TAjh0+F1tw8HyTIDyJVSHpRSNgPvAZ36Gksp86SUuwE3q5bqH66dkUCgrxevepLVkfMVxE+HoEjl7jjrQTUkZ/tSV0vWCSklh0qUu2hPgXMUR5tRcqCkltTYzqVPSe6QkntwHVTlw7Sbut8mZiz4DXJenCNntVIai5Yo10/6//q+r7ZWdcHva3wDlMKJGdt7ZpWxzf5UXDNRqVBx2G3duWZ6sjiWA+EdXnf3+MBBssTRuXV7gWmZzQgh7hBCpAsh0ktKPCwm0AOhgT5cNX0YK3cVcqzKjQrGuqOmSHUZHXneiWUpZ6kq3u+fUV1L3YSSmibqmlW6824nWRxHyutpbjUyoovF0V7L4co4x/Y31DCh0Rd2v43BSxXSOcviyP4SkubC+Msh+Qz49i8qwN0XivZAS73thX9diZuqFFBPMZfKw9DW5BjFETlCZWdV5Nm/LyfSreKQUhqklMUdXnf38Oo/ca1DSvmylDJNSpkWHW1lfxoP4dbZyRil5PWNea4WpXdyTX7qjhk6ZqujplBdrNyEg6a7/dAAH/YUVDrlGDmm4U1dXVXhgT4M8vd2XWZVbQlkroLJ1/Y+ryJhpspUqndw1+bSXJXSOvJ89R05/69qfvd3T/Vtf0e2qmdbC/+6Ep+m5CjvYcSBPT2quhJpbnbo3im5NiY3O5WjwLAO7+NNyzQdGBYRyMIJQ3hnS75Tg7gOIftLCBmq/MwdST4TEk43WR3uYTmZL9oXTBhCXlk9VfV2+tctYB4X29XiEEKQHOXCzKpd74CxxbqGfgmz1LO5IttRZH+pnkeabjIGj1dB+q0v9y1YnL9ZZSmFxtsnlzlAXtCDu8qsOPoyh6MrkaY+V24e57C2V9WVQojzOrx/VAhRIIT4SggxxEGy/AikCiGShRC+wNWAnvVhgdvnplDT2MqyH+0YytjS4NyLdmszHPgWUs+FrvO/hICzHlKFZtted54MNnCotA5fbwPnj4sFYK8TEhByi2oZEupPiL/PSeuSooLIK3VecLygop6z//EtB0pqO6+QUsWbhs20ztUSN03N6HB0nCP7SxVPCEs4sezs36v01NWP2L6/I1vti2+YiR4NPkE9B8hLslTtS0CY/ccLCIOg6AFjcTxmfiGEmAo8BDwH+AD/cIQgUspW4B7gKyADWCal3CeEeFwIcbHp2NOFEAXAYuAlIYSH9T9wDJOHhTE9KZxXNxyita9dVd+7Ft5e7FjBOpK/UbWoGLnA8vrkucqfveGfbmF1HCypIykysH0q324nBMhzimtPsjbMJEUGUVjVQGOLc9rKbMwt42BJHat2H+u84vBGdZHqKSjeEZ8ANYLVkXGOxiqliEae33l5cAyccR9kfwEH1lm/v6oCqC5wjOIweMHQyT0rjtIsx8Q3zESOUK47N8ZaxZEImOwxLgU+kVI+BdyLanboEKSUq6SUI6WUw6WUT5iWPSqlXGl6/aOUMl5KGSSljJRSjnPUsT2N2+emcLSygS/39aGvTVWBagOS971KI3QG2avByw9Szux+m3kPQm0RpL/mHBls4FBpLclRQYQF+pIQEcieo5UO3b/RKMktriU1xnIz6eSoINUB3EkpufuPVQPwfW5p5xXb31CZUmMvsX5nCTPVTG5HKfwDa8HYenK1OsBpP4ewRPjqIZUpZQ3tjQ0doDhAWVnHd1tOIZdS/YYcrTgGiMXRCJi/8ecA35heV3VYrulH5o+JJTkqiFfW96ENyd4P1bMwwM63HC8cqDTcpDk959AnzVbZMxv+aVv76t5oqoG8H6zevLXNSH55PclRyhqYEB/qcIvjaGUDDS1tpMZ2Y3FEObfZobn2Z0d+BXXm2FhDBexfARMWg29gD5/uQsIsFRMp3OEY4bJXQ0C4Stvuio8/nPu4anG+w8oU7iNbwScQYsc7Rr64aWr0bNHek9dVFyrL2tGKo65YWWJuirWK43vgH0KIR4A0YJVp+Ug6p9Bq+gmDQfDTOcnsKqjixzwbUxb3LFftP0YugF3vWX8nZy1lB9QdU1fXgyXmPaQqy3981THHbqiENy6C1y8wFR/2ztHKBlraJCmmi/fEuFAKKhoor3NcLn1uNxlVZpIjnZeSazRKMo7VMCImmJY2yZZDpn6luz+A1kbr3VRmzC4gR8Q5jEZVvzFi/sltTsyMXaSSKdY+Yd3FNH+zuth7nRxL6hPtFeTbT15n7lHliOI/M1Hun1llreK4B2gGrgDulFKa27QuRMUkNC7g8qnxhAf68PL6HlIFu1KSpczuCYvVvIXaIsj9pvfP2UKO6YKdel7P24Ga85AyD374l/1WR0MFvHkJHN+rsrm+etCqQipzKm5ytElxxIcBsMeB9RzdZVSZCQ30ITzQh0NOCJDnl9dT29TKDTMT8fM2sD671BQUfwOGTFYV0rYQFKkulI6IcxRuV4OWuouFgUqmWPAXqC9TXQd6orkOju9xTHzDTGg8BMdazqwy96hyRCquGXOzQzeOc1jbq6pASnmRlHKSlPK1Dst/JaX8P+eJp+mJAF8vrpqewLqsYusnBO5ZrlxU4y5VFkFQtON7R2V/qVITu2td0ZV5D6mLx9ZX+n7Mhgp481KlNK56Cy5+Tt2xbXmx14+aK8bNhXjj4wYBOLSeI6eolugQP8ICTdPhpIR3r1VuOhMqs8rxFse+QhXfmJIQxmkpkWzILVV3z0V7bbc2zCTMVLO8jXY2ccj+UrX1GH52z9sNnQKTroHNL6gJhd1xdJsqoLO3fqMj5lGylgLkJZnKzRYU5bjjhSer36inWxxCiGghRHSH9xOEEH8WQlzjPNE01nD+uFjajNK6rrlSwt7lKq4QEqtM+YlXqR9vXWnvn7cGc3zBGjeVmYTTVB+rjc9BU23v23eloQKWXqKGDF31FoxaoNKAU89XBWQ1RT1+/FBpHSH+3kQGqYt6iL8PKdFBDo1znNSj6thOyPoc1v65fThSspO65O4/VoWXQTAyNoS5I6LILa6lfvOrKg4wvo+9QhNmQVOVKga0h+yvlHUQGNH7tuc8CgZv+PrR7rcxB8bj0+yTqytxU1VtRUNl5+UlWcra6Jpybg/eviohwI1rOax1VS0DLgIQQkQB61HZVS8KIe5zkmwaK5gUH0ZUsC9rMop737hwu6qAndAhDXfK9SqjZff7jhHo4LcqcGopQ6YnznpIuSK2vmzb58xKo3j/CaVhZsFflQ9/zeM97uJQaR0pUUGIDj/+iXGhDnNVSWnOqOqgOHa9D16+ajrdp78Eo5HEyCCOVTXS0OzYlNx9hdWkxgTj7+PFnNQogmjAN+MjGHcZ+A/q207bGx7aEeeoLlRuU2tvMgYNgTm/hoyVkLfB8jb5W9R89IBwy+v7SpxJERV2iHNIqSwORxT+dSUq1fMtDtRscbND8wpUM8JxwI3Az5whmMY6DAbBWaNi+DarmJbeajr2LFcXq479iGLGKDN8x9uOmYGQ/RX4hdruKohPUx10Nz4HjdXWfaar0uh6AYocDjN/rjLHesjDP1Ra1+6mMjMhPoxjVY0U19jfT+tYVSO1Ta0nmhu2tajW4aMWwvl/gYIfIf1VkqJUZtPhcsdaHfsLqxk7RCmI0YNDuDowHe+2hr67qQDCk1TRmz1xjmxTeNQW63TWPTAoHr588OT550YjFGy1vz+VJYZOUc8dv0d1peo76Mj4hpnIESrJxF5XoJOwZXSs2YcwnxMV3dvp3CZE4wLOGRNDdWMr6T1lVxnbVBpu6nknV7hOvg6K99mfXimlmqMw/Ky+ZbTMe1D9ELe+1Pu2DRWwdJFJabzd/cXnjN9AUAx88TuLP8LGljaOVja0p+KamRgfCjimxfpJPapy16iYzqRrlKsw+UxY8zipAWo7R8Y5SmqaKK5pYuxQpTiEENzo+y0HiMc41A53jnmw02E7LI6c1apS3JYLr28gzH9MWSq73u28rjRLZV05Mr5hJiBM9ZHqmFlVau5R5QSLI3KEatJYc6z3bV2AtYojB7hMCDEMOA8w5znGApVOkEtjA3NSo/H1MrA2swdfft4GlUHV0U1lZvzlqp31DjtrOo7tUm1EbLmD7Ej8NOXi2vifntMu68tNSiPDpDR6yN7yH6QuNAU/wp5lJ602xxTMGVVmxg4ZhEE4poI8p0hlVLVbHLvehcBIlYIqBFz4T2hrJnX7nwEcmlllLvwzKw6O7yWxMYO3W84is6gP8aSOJMxSFdqVfcjIb2lUbs2RC2yPD0y4QtV8rHm8c0zMHN9wZEZVR+LTVGaV2TJvHxfrBIujPSXXPeMc1iqOPwJ/A/KAzVJKc4ez8wEHVQFp+kqwnzenpUT0HOfY8wH4hli+qAeEwZiLVeDcnmrg7K9oH9rUV856EBorYUs3Vkd9uUq5tUZpmJl0jXLHff0HFbzvgDmjKqWLqyrIz5sRMcEOmc2RW1xLZJAvEUG+ylLK+kIpcLNVFjkczvgNPlkruSRwt0MtDnPh37ghyoJi+1Kkly8ftc1hQ66dIwfsGeyUt0HdUdsaC4MT3XNrizplpXFkKwRGQUSK7fu0hrhpqjCvqkC9L8kG32DVTNHRtM8fd884h7XpuB8BCajiv44J19+g2o5oXMz8MbEcLK3jYNcmdqBaJexfCWMuVL2GLDHlOnWXn/l534XI+Ur9uILtaGU/dAqMugA2/efkDJZ2SyMTrn7HOqUBaiTnwqeUNdSlDuCQyeJIijq5wn1CXBi7Cqpsr8zvQqceVfs+UbMbJl3deaPT/w+ix/Awr1FY4qAMN1R8Iy4sgNBAH3VTsPs9xJiLiY4Zwvc5dh4ndry6GelLgDz7S5XVlTSnb8ceNl0p303/OWHx5G9W1oYjM5w6EjdVPZvjHObAuDOOFzJENVcszeVoZQNf7+85M7C/sWV0bJGUcgcQLYQwmJZtkVJmOk06jdWcPToGgLWZFqyO3G9U6uSEHlIvk86A0IS+u6tqS5T/t69uqo7Me0Apsc0vnFhmVholWUpppNpo1cSnKctj0xIVdDRxqKSOmBA/gv1OrlqeGB9KaW0Tx6v7HiCXUpJTVHOi1ciu95RrY8jkzht6+8JF/yLaWMzCEgdV0aMUxzizm2r/SnVep97InNQoth4qt6+pope3uoDbanFIqW4yUuapliJ95Zw/qOdvHlOB6vIDzgmMm4mdoJJLzBMBHTX1zxJCQORwZGkOdyxN5/al6SxZ5z7Wh7V1HD5CiKeEEDWoGRlJpuV/E0Lc5UT5NFYyLCKQUbEhlt1Vez5QJnzyvO53YDCoQT4Hv4XKfNsFyP0akNZVi/fGkEkq82vz88q1c5LSmN+3/c5/TP3wV/++fZGljCozE0wBcnviHCU1TVQ3tqrmhuUH4chmZW1YuktNOI09Qy7nqrbPacjrZVypFdQ1tXKorI5xQ81uqjdUcVnSXOamRtHUauw5ocIaEmapBAVbJvWVZKrvmL03GWHDlKW2d7myPMA5gXEz3r4weKK6QWqsUoFrZykOgKhUagsz2VdYzYS4UP7+VRYvfneg98/1A9ZaHH9A1XFcD3RsEbkVuNnBMmn6yDljYvgxr5yqhg5DiJpqlE993KXd9wIyM/laQMLOd3vezhLZX6n0TFvbV3THvAegqRrW/cUxSgMgZDCccT9krWpvs3KotI6UaMuKY+yQQXgZhF1xjk4ZVbveBwRMuLLb7Y9O+y1lhMJnv7K7h1jm8WqkNAXGc76Bwz+oYU0GA6clR+LjJfjeIXEOCUd+tP4z5qFNjrjJmP1L9b3b8E91U9DVknM0cdNU9mHRfvXeGYFxE/UhSQQ2HOXM4SF8fNfpXDRpKE9+kcnL612vPKxVHNegelStADrmNO5FNTrUuAHnjImh1ShZ37GKPHOVKoKzlE3VlfBElRq6823b8sfbWlRrbEtDm/rK4Akw5iJVEFiSBdfYqTTMzLxLBU+/fJCqmnrK6pq7tTj8fbwYGRti1wxyc0bViJgglU2VciaEdh9MjR8yhMdabiSgdI91ack9YG41Mr38M3jnSogZB9NuBlTwf2pCOBvsjXPETVPV3LbEObJXqzv3QUPtOzaAX7CqKAelNOxxfVlD3DQV1M8wVSQ4o/jPxMf5gXgheXxuMN5eBv555SR+MnEIf1mVyX+/t6E/nROwVnEMBQ5bWO5temjcgMnDwokI8mVNRodA2p4PVOzCWt/vlOuh8jAc7qYy1xL5m5R14Ij4RkfOfkRZMNe8o1JXHYG3nyq6K82mdsPzACfVcHRkYlwoewoq+xwgzymuJTTAh+iKHeq8Tuq5S09SVBCrjKeRFzFHdYPtS6qriYyjlfze/wPCvrlXxRNu/bJTa4+5qVHsK6ymrNbCnAlr8Q1S/yNr4xz15cpd11NTQ1uZdI3KCpx8reP22R3mVia7l6l5M+FJTjnMtsPlvHdQzX9PlGqCtreXgX9dNZkLJgzmz59n8NqGHnp2ORlrFcc+4AwLy68EehiNpelPvAyCeaOiWZdVoiYD1pUqS2DC5dZbAmMuUpXfO962/sDZX6lxoinz+iR3t0SPgp+td5zSMDNyAQw/h5ht/ySSqm4tDlBxjor6Fgoq+pambO5RJXa9p7JkOlbtWyDYz5voEH/ejvw/QMKq+/tW0d/SyILsR7iNj2HqTXDt+ye1F5mTqrLffjhQZvv+O5IwS2UaWRp01JUDa0EaHXuTYTDAVW9C2i2O22d3RKSoNjH1parWwuDl8EO0thl55JN91IckqQUdUnK9vQz86+opLBg3mMc/288bG/McfnxrsKWO499CiIcBL2CxEOJ/wAPAn5wlnMZ25o+Jpaqhhe35lbDvY9Up1Bo3lRmfABh/mRrwY+0gmZzVKq3Sz0NmegkBC57E0NbAb3yWkRDR/RAjcwV5X/tW5RbXMibaR6Xhjr1YuVZ6ITkyiJ01IXDWwyoesH+FbQetL8e4dBFnNq9nbfxdcNG/LFbyT4gLJTTAhw05DohztDVB4c7et83+UiVqDJ1q3zFdhblTLjgtMP72lnz2H6vmvovSVDv3Lu3VfbwMPHfNFM4dG8sfVu7jzU15TpGjJ6yt4/gUZV2ch4px/AFIBS6SUjp4mIPGHuamRuHjJZS7au+HquFbrI0TdqfcAK0NsPej3rctP6TSEh3tpnI20SP5LvRSrvT6Ft/iXd1uNmpwCD5eok+ZVWW1TZTXNXOW2KbSobvWbnRDUlSgqh4/7U7lBvrid9Yr8bID8N/5ULiDe5p/QfW0e7q1Nr0MgtOHR7Ihp9S+WpVh5kLAjT1v19aqkhJSz1NWgqdibnjoyOFNJkpqmnh6dRZzU6NYOH6wanNioQjQ19vAkmunMn9MDI+s2MfbWyxFEpxHr/89cyoukCmlPFNKGSylDJRSzpFSWjdiTdNvhPj7cFpyJHv271Wxh55qN7ojbqpSODutcFfZMrTJzXiRK6g1hMIXD3TrDvLz9mL04EF9mkFuzqiaVPalqi5OmmvV55KigiitbaKmRSproa4Yvvlj7x/M3wKvngsNFayf+V8+M846UcPRDXNSoyisauRAiR3V6sHRqtK5tzhHwY8qbdfTbjK6Yo5zOMHiePKLTBpb2njs4nGqW3Pk8G7bjvh6G1hy3VTOHh3Dwx/v5d2tfUij7yO9Kg4pZQtwF+CkcswTCCEWCCGyhBC5QogHLKz3E0K8b1q/RQiR5GyZPJFzxsQwscJkCPZFcQihKskLflRV2j2R/ZW6aEQOt/04LkRKyd5ywbfD7lTB2j3Lu93WPIPc1rvynOJaoqgi4th6mHil1f5w8xjZw2X1qpL+tDsh/TXVUqM79n2sRub6h8Jt3/B90wj8vA09xm8A5o5QcQ6HuKvyN/ecjZf9pcrA6m1ok7szYj5c9JzqcOBAfswr58PtBdw+N4Xh0SaXZlSqGjdQX27xM37eXrxw/VTmjYrmwY/2sOzH/pnkba29+BXg1P+2EMILWIIaRzsWuEYIMbbLZj8FKqSUI4B/ovpnabpwzuhYLvbaRHHoxL5nfUy8Sv3Id/ZQSd5UC3nf963fkJW0GR3Q6t0CxTVN1De3UT3qSuUO+vrRbkfXTowLpaaxVV3IbSC3qIYr/DYjZBtMtM5NBSfanxwy96w662FlsXz6S5X63BEpYcOz8MHNSsn89BuIHM6+wipGDxmEt1fPP/GEyEASIgLVVEB7SJileoyZO8ZaImc1JJ7e9xkg7oLBS7Wk9/Z12C5VQHwvQ0P9uefsESdWtPes6r52w8/bixevn8YZI6P53Ue7+SDd+crDWsWxBviLEOJZIcQNQojLOj4cJMsM1JyPg1LKZuA9YFGXbRYBb5heLwfOEcJZjWk8l4S2w4w1HOYL0cc+QADBMUoh7Hr/5IuVmUPfQVuz9T2jbOTz3ccY++iX7Y36HMlBk2smKTpU9bGqKYTvn7G4rXkGua31HDnFtSz22aAu6DHWF4olRqpgfXuzQ79g+MnTqkJ743MnNmxrhc9+Dd/8QXU4vnEFBEUipew0g6M35qRGsflgee/zXHoiYZZ67q6eozJfye/INNwBxJubD5N5vIZHLxpLoG+HCodIc5fcntuN+Pt48fIN05gzIorffribD7cVOFFa6xXHf4AY4P9QF+7lHR4fOEiWOKCjqiwwLbO4jZSyFagCIrvuSAhxhxAiXQiRXlJipwnuiexZjhEDzxdPoLqxm4u+NUy5XvnXc762vD77K9XkLuH0vh+jG7YdruDXy3bS1Gq0vxmfBcx388nRQcrNMmExbPy3xXnWqbHB+HkbbJ5Bbizax/DWA73WbnQl0Neb2EF+7Q0YATX0aczFahRu+UHVEeDdq2Db/2DOvXDZf9uL3woqGqhubO01vmFm7ogoapta2Xmk0iY5OxGRouaedBfnMA9tcqJ16qkU1zTyzOpszhgZzfnjBndeGZ6oLH8r2qv7+3jxyo1pnD48kvuX7+KTHUedJLH1WVWGHh6OT2S2Eynly1LKNCllWnS0HZ1aPRHTXPGaoadTZAzl+2w7Lrqp56qLgaUgecehTQ402QHyy+q5Y2k6Q0L9GRrqz7bDdvZTssCh0lr8vA0MGWSqNJ7/R+WC+OqhkwLlPl4Gxg4dZFNmVWV9M/Ma12IU3soasJGkyKCT26svfEq11fjkbnhtIRxYp3zt8//QKUvppBkcvXD68CgMAvsUtHmwU3cWR/ZXEDEcokZYXn8K8+SqTJpajfzRHBDviJePcjdb2V7d38eL/944nZnJkdy7bCcrdjpHebhTTtxROk8TjDcts7iNEMIbCAXsrF4aYBzdBhV5BKddQ1igT+cqclvx8oFJV6mgZm2X5onH9yj3joMzZKrqW7jl9a20GiWv3TydmcMj2ZFfYXdr866YmxsaDKYfamicmkCYtarzjAcTE+NC2Xu0CqOVMZec41Vc6rWBsqFnQlCUzfIlRwWR1zWmMmiIaq+RvxEq8uC6DyyOf91XWI1BwJjB1imO0EAfJsaHOSBAPku5pKq6/Gyb6+DQeu2mssCWg2V8tOMod5yR0n0iQ2Sq+r0V7VMDsHohwNeLV29OY3pSBK9vzHNKnNBqxSGEuEQIsV4IUWp6fC+EuNSBsvwIpAohkoUQvsDVnBhRa2YlYP6lXAGslY6+ong6ez4ALz+8xl7EWaNiWJdVbN8XZ/L1YGyF3e93Xp5jcj3YM7SpC82tRu58axv55fW8dMM0hkcHMzUhnNLaZvLLHTcVD+Cgpa64p/8Cxl8Ba/6oWpB3YEJ8GHXNbRy0cshSzf41xIpKDFbWbnQlKSqI8rrmzg0rAdJ+Cuc9AT9dDSPOsfjZ/YXVpEQHE+BrvTNgbmoUuwqqTj6eLZg70x7p4q46tF4VCDopFuaptLQZeXTFPuLCArj7rB4ssSGTlHvyhdPhicHw7AR481JY9VvY+oqqxq880imjLdDXm9duns7rt8zAy+D4MLBVfaaEEPcBfwGWAq+bFs8C3hFCPCKlfNpeQaSUrUKIe1AZXF7Aa1LKfUKIx4F0KeVK4FXgTSFELlCOUi4aM22tqmhv5HngH8rZo2P4eMdRduRXkJYU0fvnLREzWhU87XgLZnUoJsterYK+IbEOEV1KyUMf72HTwTKeuXISM1NU6GpaYjgA2/MrSIzsObXUWlrbjOSX1bOgqz9ZCFi0RN01f3SHats9dArQsYK88sRQph6IOvghVTKI8MkX90nGJNPfmldax6RhYSdWGAxw+j09fnZ/YZXN/+85I6L499pcNh0oY8H4wb1/wBKDJ6q2KvmbO7vnsr90WizMk1m66TBZRTW8dMO0npX8mb9VMa6yXPUozVExjyNbobnD4DbvgBOp8VGpBEWmqt9vgIM6VnfA2gaF9wP3SClf6bDsNSHEVuBxwG7FASClXAWs6rLs0Q6vGwEb+mecYuR9r4LZphYjZ46KxtsgWJNZ3HfFASpI/tmv1ByC+GmqB1bBj3Dm7xwjN7BkXS7LtxXwy3NSuWxqfPvykbEhBPt5s+1wBZdOie9hD9ZTUNFAq1Fadg34+MPVb8Mr58C718Dta2HQUIZHBxPg48WuI1W9y9FUw6iK71gbcA4LffvWrdUsW15ZF8XRCxV1zRRWNVodGDczJSGcQF8vNuSW9F1xeHmr4rj8Tby1+TA/5Jay5JopGLJXOyUW5skUVzfyz6+zmTcqmvPG9nLzZfCCoZPVoyNSQs1xpURKc1TKblkOHNuluvdKo2rtcsc6h8tvreIIBiwdfZ1pncYd2LMc/Aa1V3EP8vdhRnIEazKK+N0CO+YGjL8MvnwQ4463eHirL2c0rGEh0mHxjRU7j/L06mwunRLHr+andlrnZRBMHhbG9sOVDjkWnMio6m4OB8Exqingq+fBO1fBrV/i5RvE+LhB1vWs2r8SP9lE9uCfsLCPMppTcg/ZOH/c1sC4GV9vAzNTIu1vs54wC7n+KZ5e+SOVxgC2p39PWk2hjm904S+rMmhuNfLYRRYC4tYihIp7DRoCyV160LY2Q8Uh1QLeCVgb4/gEFVPoyuWcHIfQuIKWRnWXMbrzXPGzR8eQXVTLEXtiBP6hMPZiWna+z8dbc2jN/IJyEcbmxmG9f7YX0vPK+c3y3cxIiuDJyydY/BFNTQgj83g1tU32DTYyY45T9NROndixcMVrULRXua2MRibEhbGvsEp1Hu6B1h3vcMgYi29i36fR+ft4MTTU3+aiQ3PNi7U1HB2ZMyKKvLJ6u74rzXEzENLIGQGHiAzy5cjmT9QKW0f9DmA2Hyzjk52F3HlmisVZ9w7B21e1RDG5Wh2NtYojF3hACPGVEOIx0+NL4EEgSwhxr/nhFCk1vZP7tZqJ0aXFyPwxygy2K7sKOBB/CX5tdTyUmMkC//1sMkzl6le28uBHu/scUM0rreP2penEhQXw0g3T8PO27OedmhiOUcJue+oMOnCoVM3ICA88uWNsJ0aeB+f/FTI/gzWPMTE+lMYWI7kltd1/pjIf7/wNfNQ2l9RY+7oFJ0UF2W5xFFYzeJA/kcF+Nh9vbqrK/rKnivzfWaG0SgP3ji7j6hnDSCxbT3PsFGXFaWhpM/KHFfuIDw/g5/M8NzXZWsVxM1CBmvZ3k+kxyrTsFuAXpkfPUTuN89jzAQRFqwl+HUiKCiIlOog1mRZmkVtJfXMrd3znTyExXF/7Gj4t1cxfdAN3nJHC+z8eYf4z3/HFnmM2pcxW1jdz6+tq3Oj/bp5OeFD3/u8pw1SA3FH1HOZUXKtcBKf9TGUy/fAvTq/+AuhlBvnuZQB8bJxDaqx9XtykqCDyymxTHPsKq22Ob5gZERNM7CC/Prurfswr5z8bizgemEpS7R6unxDEZHGALT7T+7S/gcgbG/PIKqrhDxeNsynrzd2wtgAw2cpHirMF1ligsRqyvux2rvj8MbFsPljWZ1fPnz7L4GB5A62TrsVQVwIGH/xGzuehC8aw4u45xIT48fO3t3PHm9s4XtV7nnlTaxt3vLmNgooGXr4xrVdzPTTQh9SYYLbnO0hxlFhIxe0OIWDh3yDlLKK/+x1n+WV1P4NcStj1HodDJlPiNZj48O7nfFhDcmQQlfUtVNY3W7V9Y0sbB0pq+6w4hBDMGRHNDwdKbU7hrmtq5b5luxgWHkjsuHlwNJ0hx9ZiEJIXCkfQ2NLWJ5kGEoWVDTz7TQ5nj45h/hjPtsCsUhxCiNAe1mll4WoyP1d58t0MbDp7dAwtbZLvs20v8Ppq33He3ZrPz84YTsJZPwUEJM5qb1Q3IT6UFXfP5sGFo1mfXcK5z3zHm5sPd1soJ6XkwQ/3sPVQOX9fPJHpVmZ7TU0IZ3t+pdUFeN3R0NxGYVWj9YoDVCHk4tcREcN5zvAMJYf3W97u6HYoy2GNz9kMjw62O3/+pGaHvZB5vAajtD0w3pG5qVFU1rfY3B/siVUZHKmo5+nFk/BJPl3Nud/wDE0BsWysj2PVnmN9lmkgkFNUw+IXN2GUkj9cNLbvAXE3wVpX1W4hxEmjY4UQtwI7HSqRxnb2fABhCRBv2SWQlhhOaICPze6qoupGHvhwN+PjBnHvuSPVMX7yNJz1+07beXsZ+NmZw1n96zOYOCyURz7Zy5UvbSK3uOakfT63JpePdhzlvnNHsmhy11Zk3TMtMZyqhharC/C6w+z6sUlxAASEwbXv4+Vl4Lflj9JcY6HN9a53wduf9+qm2u2mUjKamh1a6a4yX+zHDe32Pq9XZo9QcQ5b2o+syyrmnS353DE3hRnJEScaHlbk4Tv6fFKiglm6qX8HDbkTGw+UctkLG2luM/L+HbMcVo/kSqxVHO8A3wgh/iKE8BJChAshPgSeBX7lLOE0VlBbAge/VRXP3dzFeHsZ1CzyTOuryI1Gyf0f7KKhpY1/XT0FX2/TV2X6bZBwmsXPJEYG8dZPT+PvV0wkp7iWC/61gWe/yaapVbkpPt5RwD+/yebyqfGdW0dbwdTEMAC22xnnaG9u2JdslohkdsxaQhwlNL97Xeeuwa3NsHc5rakLya4ykGpFkWBvDIsIxCBQ0wCtYH9hNSH+3sSHB/S+cTdEh/gxZsggvrey/UhlfTO/W76bkbHB/PrckWphSKxqegiIUQu4fmYiO49Udu/iG8B8uK2Am17bypBQfz6+63QmxPddqbsT1sY4HkSNjb0e2ArsRvWSmiqlfM154ml6Zf8nVs0VP3t0DGV1zeyyssPraz8c4vucUh65cOyJoTJWIIRgcdow1tx3JgvGD+bZb3K48LkNLN2Ux++W72FmSgR/vcxy2m1PpEQFExrgY3ecwy7FAcRPPpsHW24juHAjrLr/REPEnNXQUMGRBFUpPiLG/vnrft5eDA0LOLnZYTfsM7VSt9cNMjc1im2HK6hv7j0m9uiKfZTXNfPMlZPx9+kQ7E08Hbz9IflMLp8WT4CPF0tdMBvbVUgp+dc3Odz3wS6mJ0XwwZ2n2x3zcidsaXK4AfgCmALEAo9LKa1r2ahxHvs+Ns0V7zrzqjPzRsbgZRBWpeVmHKvmqS+zmD8mlmtnJPRJrKhgP567Zgr/u3k69c1tPLpiH/ERAbx4/bQT1osNGAyCKQlhdmdWHSypI3aQH0F+1ta+diYhIpBvfM9mXcwNsO112Py8WrHrXQiKZof3VACHuKrA3Oywd8XRZpRkHq+2K75hZs6IKFraJFsOWZ46Z+az3YWs3FXI/52Tyvi4LnfSZz8KN30GfkrhXzIljpW7Cqmosy7Q78k0txr5zfLd7db167fMIDSgl9RvD8Pa4PhIYAtwLjAP+BPwkRDin6aGhBpXUFsMhzfC2N77IYUG+pCWGM6ajJ7jHI0tbfzyvR2EBvrwt24K8mzhrNExrP71GTx64Vje/OlphAX2/esyLSGcnOJauxrxHSqt7bO1AcqimhgfxjOti9V8jK8ehp3vqLbhE64ku7QRXy8DiRGOubtMilS1HL2lOh8qraWxxWhXfMPMjOQIfL0NPablFlc38vtP9jJpWBh3zbMwNjgkFoadiLndOCuRplYjy508YMjVVDWo7s7LtxXwq/mpPL14Yp9ulNwda/+iHUAGMFlKuV5K+SfgDOAnQLqzhNP0QubngFQXMCuYPyaWzOM1FFR07zN/8otMsotqeXrxpD4VkVkiyM+bW+ckExfWd987qEJAgB12uKtUDYd91sCE+FAyi+povOh51T/ok5+DsQUmXU1ucQ0p0UG9jmy1lqSoIGoaWynv5U59X6FqNdLXVNyO+Pt4MT0pvFvFIaXkgY/20NDcxj8WT7Lqbx0zZBDTk8J5a0v3GXeeztHKBha/uJEtB8t5evEkfjV/pMdnT3WHtd/un0kpr5dSVpsXSCm3AFNRMQ+NK8hYqYKQseOs2vxsU+742m6yq9ZlFvP6xjxunZ3MmSPdbwDWpGFhGARsz6/s0+cr6pqpqG8hxc42DxPjQmlpk2SVtcE176l54EMmweAJ5BTXWtU911qszazaX1iNr5fBYceeMyKarKIaiqtPrstZln6EtZnF/G7BaJuOd8OsJA6X1fOdvXM/3JC9R6u4ZMkPHKtqZOmtM7himmMacror1gbH3+pmea2U8jbHiqSxioYKNedgzEXdZlN1ZXh0MMlRQRbdVaW1Tfxm+S5GDw7htwtGOVpahxDs582owYP6nFl1qK+puF0wZ8bsPloFIYPhrk1wwyc0thrJL68n1QGBcTPm1M3eMqv2H6tm5OBgfBxk6XTXfuRIeT2Pf7qfWSmR3Hx6kk37XDBuMFHBfrzphNRcV47lWZNRxJUvbcLXy8CHPz+d00fYPrjL0+jxWyaEeEcIEdLh/Z1d3ocLIdY7U0BNN2R9oQYsjVlk08fOHh3DpgNl1HWoIpdS8tvlu6lubOVfV0/pnB3jZkxLDGPnkco+DafK6zhn3A7iwgKIDPI9MYPcPxQCI8gtrkVKxwXGAYaFq5TcnjKrpJTtGVWOYuyQQUQE+Xaq5zCnaAsh+PviiSemJ1qJr7eBa2YMY11WsX1NN7tQ1dDCBc9t4K9fZDhsn9by5ubD3L40nZToID6+63RG2tmfzFPo7fbkKqCjY/opoKMPwxeY7WihNFawfyUMioe4qTZ97JwxMTS3GTvdSb61JZ+1mcU8uHA0owa79xd/akI4tU2tZBedXFzYG4dK6/AyCIbZmRYphGBCfOhJPatyi1XzQ0fUcJjx9TYQHx7Ybi1Z4nh1I+V1zQ4JjJsxGASnD49kQ25p+938az8cYsuhch69aGyfU0uvPS0BgxC8tdkxVoe66dlFxrFqXll/kJw+fC/6gtEo+cuqDB75ZC9njYrh/TtmETOob7NXPJHeFEfXW4qBGenxNJpq1LhIG9xUZqYnRRDi792elptbXMOfP9vPmSOjbXY9uIKOEwFt5WBpHcPCAxyS5TIxLpSc4loamk/0YMoprsHbIBxeGZwUFdSjxbG/sG8zOHpjbmoUJTVNZBXVkFNUw1NfqRTtxXb474eEBnDumFjeTz/ikP5Vr/2Qx1f7irjnrBEE+Xnz1y8y7d5nbzS3GvnFuzt4ef1BbpiZyEs3TOtzerenMvDyxE4Fclar3lRWpOF2xcfLwJkjo1mbWUJjSxv/9+5Ogvy8+fviiR6RAZIQEUhkkG+f6jlsam7YCxPiw2gzSvYfO2F15BTVkhQV5PD0y+TIQA6X1Xfrx99XWI0QKnPJkcxJVc6Fb7NKuHfZLoL9vPtUvNmVG2clUlnfwqe7Cu3az/b8Cv66KoNzx8Zy33kjueesEazNLGajHW3hreGV7w/y+Z5jPHTBaB5fNM5hGXSehDV/8cDMnfNk9q9ULdSHWW790Rvzx8RSWtvE7UvT2X+smqcun0hMiGeY2UIIpiaGs8PGzCoppUNScc2YZ5B3dFflFtc61E1lJikqiNqmVkprLafk7i+sJikyiGAH3/XGhQWQEh3EP7/OZs/RKp64ZDzRIfanaM8aHsmImGDetMNdVVHXzC/e2cGQMH+evmISQghuOj2JuLAAnliV4bSU38NldTy3JocLJgzmjjOGe8TNljOwRnH8VQjxnBDiOVRM4w8d3j/hXPE0J9HSADlfq0l/hr4Fsc8cGY1BqEZ2189MYH5vM4/djKkJ4RwqraOstsnqzxRVN9HQ0mZ3YNxM7CB/YkL82vsvNbW2kVdW5zTFAd2n5O47VuXQwHhH5o6IoqnVyKVT4lg4YYhD9imE4IaZiewuqGJnH4ZzGY2Se5ftpKSmiSXXTiXUNJDL38eL3y4Yxb7Caj7ZedQhsnZESsmjK/bhbRA8eqF1KfADld4Ux3pgODDB9NgIJHR4P9y0jV0IISKEEF8LIXJMz+HdbPelEKJSCPGZvcf0WA6shZa6PrmpzIQH+TJ7RBSpMcE8fEHPrUrckWnthYCVVn/mYKkKXNtbw9GRifGhKiUXFXg3ShjhhKya5Mju26tXNbRwpLzB4fENM4vThnH+uFgeu8ixF8rLpsYR5OvVp9Tcl9YfZF1WCb+/cAwT48M6rbto4lAmxofy9FdZDp8BsmrPcb7LLuG+80YxONQzLHRn0aPikFLOk1Ke1dvDAXI8AKyRUqYCa0zvLfF34AYHHM9z2b8S/MMgaa5du3nphml8cvdsj5xCNjE+FG+DYJsNAXJ7mxtaYkJcGAdKaqltaiWnyPEZVWbiwwPwNgiLAfKMY84JjJsZHxfKSzektd/VO4oQfx8unRrHp7sLe62K78iWg2U8vTqLn0wcwg0zE09abzAIHrpgDIVVjbz2wyGHyVvT2MIfP93HuKGDuHHWycc91XCXqM4i4A3T6zeASyxtJKVcA/RPvp070tqs6jdG/0QNF7KDQF9vj80E8ffxYtxQ2woBD5XU4e9jYLADUyYnxociJew7WkVOcS0G4VjFZMbby8CwiECLrqr9Dmw10t/cOCuJ5lYjy9KPWLV9aW0Tv3h3BwkRgTzZQ5B+Zkok88fE8vy6Aza5M3viH6uzKalt4olLJ5ySwfCuuMsZiJVSmkeEHUd13+0zQog7hBDpQoj0kpIB1N7g0HpoqlJpuKc4UxLC2VVQSUub0artD5XWkRQZZHPRWk+YO8LuOVpFbnENiZFBTiueTIoMtFg9vq+wmqhgP49JbujIyNgQTkuO4K3Nh3st6GwzSn713k6qGlpYcu1UQvx7vnF6YOFoNUtmTY7dcu4pqGLppjxumJnI5GFhdu9vINBvikMI8Y0QYq+FR6fSZ6lyDu1KiZBSviylTJNSpkVHu1/PpT6TsRJ8gyHFEd5Bz2ZaYjiNLUYyj1lngB4qrSPFQYFxM9EhfgwN9Wd3QRU5RY7tUdWVpKggDped3CV3X2GVR1obZm6clURBRQPfZvXctfnfa3PYkFvK44vGWeWWGxETzDUzhvHOlnwOlNT2Wb42o+ThT/YQGezH/ee7ZyseV9BvikNKOV9KOd7CYwVQJIQYAmB6tm3G6amAsU11wx15Pvh43t2lozF3yt12uOeZEQAtbaqHlDPcSBPiQ9meX8GhUudkVJlJjgqivrmN4poTrpem1jZyi2s9WnGcNy6WmBC/HkfLbsgp5V9rcrhsahxXpg2zet+/mj8Sfx8v/mZHUeDbWw6zu6CKRy4cy6BerJxTCXdxVa0EbjK9vglY4UJZ3JPDG6G+1OoW6gOdoaH+DB7kb1Wn3IKKBlqN0mE1HB2ZGB/Wvn9H9qjqSpKFzKqcolpajdJpgfH+wMfLwDUzEvguu8Ri8L+oupFfvb+DEdHB/PmS8TbVTUQF+/HzecNZvb+ILQfLbJatuLqRv3+ZxdzUKC6a6JhU5IGCuyiOJ4FzhRA5wHzTe4QQaUKI/5o3EkJ8D3wAnCOEKBBCnO8SaV1Bxko1inPEfFdL4haoQkDrJgIeMqXiOsXi6DD5zpFdcbtilr3jxfVEYNyz51hfe1oC3oaT+1e1tqnWHnVNbbxw/VQCfW1P5rh1djKDB/nzlz4UBf7p8wya2ow8vsg2hXUqYJfiMMUtDtgrhJSyTEp5jpQy1eTSKjctT+/Ytl1KOVdKGS2lDJBSxkspv7L32B6B0QgZnyql4ee8u1pPY2pCOEcrGyiyMDOiIwdL1MXWkTUcZsyKQwhsms1uK0PDAvD1MnRqdrivsIogXy+HTRt0FbGD/Dl/3GCWpR/p1Pvrma+z2XqonL9cNr7PM9wDfL24//xR7Cqo4rM9x3r/gIn12SV8uquQu+eNcMoNh6djr8XxIw4oANT0wtFtUHNMu6m6YI5z9JaWe6i0jrBAH8KDHD/lODzIl2ERAQwLD3RqTYyXQTAsIqCzxXGsmjFDBjk0U8xV3DArkerG1vb+Vesyi3n+2wNcMyOBS6fYNxTp0ilxjB0yiL99kWlVUWBjSxuPrNhLSlQQd85LsevYAxW7FIeU8kEp5S2OEkbTDRkrwOCjAuOadsYNHYSvt6HXTrmqR5Xz7hpvnZ1ssRjN0SRHBZFnSsk1GiX7C6s9Or7RkdOSIxgZG8zSzXkcrWzg18t2MnbIIP5wkf2dDbxMRYFHKxtYuimv1+2fX5fL4bJ6/nTJePy8Pa9Atj9wlxiHpjukVNXiKfMgIMzV0rgVft5eTIgL7TXO4WzFccvsZG4/w/l3pomRQeSV1WE0Sg6X11PX3ObRGVUdEUJww6wk9h6t5pqXN9PaJnn+uqkOq4uZkxrFvFHR/GdtLhU9VKrnFtfywncHuGTyUGafApP8+opVikMI8Vo3j1eFEEuEEL8WQgx1trCnJMd3Q+VhXfTXDdMSw9l7tJqmVssuiPrmVo5VNTolvtHfJEUF0dRq5Hh144AJjHfk0ilxBPt5k19ez1NXTGxv7ugoHlw4htqmVv69Ntfieiklj3yyF38fLx7+ief1cOtPrLU4ooHLUK1ARpgel5iWjQJ+C2QJISY7XMJTnYxPQRhUmxHNSUxNCKO5zcjeo9UW15tdO85Ixe1vzM0O88rq2FdYhbdBODUFuL8J9vPm8UXj+OPF47jAQZ14OzJqcAhXpg3jzc15HLbQvuWTnUfZdLCM3y0Y7ZD28QMZaxXHD8AXQLyU8gwp5RlAPLAKWA0kAp8D/3CKlKcy+1dC4mwI0mazJaYmmDvlWnZXOaO5oatIilLZU3ml9ew/Vs2ImOAB54O/bGo8NzlxEuW9547E22DgqS+zOi2vqm/hz59lMHlYGNfOSHDa8QcK1iqOXwKPSynbm+WYXj8B/FpK2Qz8DZjscAlPZUqyoDQLxi7qfdtTlJhB/sSHB3Qb5zDXcJgvup7M0FA19lZZHAMnMN6fxAzy52dnpvD5nmOdvjN/+yqTivpmnrh0/IDIUnM21iqOYMCS7TjYtA6gGvDMdqvuyv6V6nn0ha6Vw82ZlhjO9vwKi6NVD5bWMSTUv0/FY+6GwSBIjAjkx7xySmqaBlR8oz+544wUYkL8eOLz/Ugp2Xa4gne25HPL7GR9Tq3EWsXxMfCqEGKxECLJ9FgMvAp8ZNpmBpDtDCFPWTJWQvwMGKTbHfTE1IRwiqqbOFrZcNI6Z2dU9TdJUUHtA6ycNfVvoBPo6829545ke34ln+0+xsMf72HwIH9+fe5IV4vmMVirOO4EvgLeAg6YHm8BXwJ3mbbJAG53tICnLOWHVEaVHZP+ThXMEwEt9a0aaIqj49+iXVV9Z3HaMEbFhnDfsl1kHq/hsYvHOnxm+0DGKsUhpayXUt4JRABTTI8IKeXPpZR1pm12Sil3Ok3SU42MT9WzTsPtldGDQwjw8TqpgryirpnK+pYBpTjMzQ6HRQQQGqC7tfYVL4PgwQtG09xm5OzRMZw/brCrRfIorFKxQohfAe9IKYuB3U6VSKPIWAlDJkF4kqslcXu8vQxMGhZ6UgX5QVNGlaPncLgSc5Bfu6ns58yR0bx2cxpTE8J1E0MbsdZVdS9QIIT4UghxnRDC81NU3Jmqo1Dwo7Y2bGBqQjj7C6s7Nck7kYo7cGodzI0Ux+sgrt0IITh7dCxhgY7vYTbQsVZxJALnA0eAf6MGL70lhFgghNBtSxxN5ufqeYxOw7WWaYnhtBoluwsq25cdKq3F2yCIDw9wnWAOJnaQPy/dMI0bZyW5WhTNKYy1MQ4ppVwnpbwdlYJ7E+CPyqgqcKJ8pyYZKyF6NETrLA9rmWIqBNzWwV11qLSOhIhAfLwG1r3N+eMGExqo4xsa12HzL8pU7LfJ9DiMUiQaR1FXCod/0C3UbSQiyJeUqCC2H65sX3awZGBlVGk07oLVikMIESKEuEUI8Q2QD9wGvAMMd5ZwpySZn4E06jTcPjAl4UQhoNEoySvTikOjcQbWZlUtBy5AVYe/DzwopfzRmYKdsmR8qjKpYse7WhKPY1piOB9uL+BwWT2+3gYaW4wkD6CMKo3GXbC24qUJuBxYLaXs1L9aCDFfSvmNwyU7FWmohIPfwcyfq1mkGpuYmhgGwLbDFQwO9QcGRnNDjcbdsEpxSCmv6/heCBEH3ALcisq4GlgtOl1F9pdgbNFNDftIakwIIX7ebM+vYIypziFlAKXiajTugi0xDi8hxGVCiFVAHnAp8CJqNofGEexfCYPiYOhUV0vikXgZBJMTwth2uIJDpXUE+HgRO0jPVdBoHE2vikMIMUoI8XegEHga2G5adYOU8ikp5SF7hRBCRAghvhZC5Jiewy1sM1kIsUkIsU8IsVsIcZW9x3UrmmrhwBpV9GcYWOmj/cnUhHCyi2rYU1BFclSQrgjWaJxAj1coIcT3wGYgHLhSSpkipfy9E+R4AFgjpUwF1pjed6UeuFFKOQ5YADwrhAhzgiyuIfdraG3U1eJ2MjUxHKOErXnlOjCu0TiJ3m5tZwFLgX9KKb9zohyLgDdMr99AjaXthJQyW0qZY3pdCBSjRtoODPavhKBoSJjlakk8msnDwtrzCgbCnHGNxh3pTXFMRwXQNwghdgghfi2EcEbBX6yU8pjp9XEgtqeNhRAzAF9Ue3dL6+8QQqQLIdJLSkocK6kzaGmEnNVqrrhB5xnYQ2iAD6kxKiCuM6o0GufQo+KQUu6QUt6Nmv73DHAxql+VAfiJpVhEdwghvhFC7LXw6JRCJNUYt5NHuZ3YzxDgTeAWKaWxG7lfllKmSSnToqM9wCg5sBaaa3W1uIMwz+fQikOjcQ7WpuM2oi7WbwohRqCqxn8N/FkIsVZKudCKfczvbp0QokgIMURKecykGIq72W4Q8DnwsJRyszWyewQZn4J/KCTNdbUkA4Lzxg7m26wSUmNDXC2KRjMg6Uuvqlwp5QPAMOBKoNkBcqxENU7E9Lyi6wZCCF/UCNulUsrlDjime9DWAlmrYNQF4K3bOzuCs0bHsOnBc/REN43GSfQ571NK2SalXCGldES12pPAuUKIHGC+6T1CiDQhxH9N21wJnAHcLITYaXpMdsCxXcuh9dBYqd1UGo3GY3CLWzIpZRlwjoXl6Si3GFLKt1BzzgcWGSvBNxiGn+1qSTQajcYqdKWZKzG2qaFNqeeBj7+rpdFoNBqr0IrDleRvhroSXfSn0Wg8Cq04XEnGSvD2VxaHRqPReAhacbgKo1Gl4Q4/B/x0B1eNRuM5aMXhKgq3Q/VRPelPo9F4HFpxuIqMlWDwhpELXC2JRqPR2IRWHK5AStXUMPlMCAhztTQajUZjE1pxuIKivVBxSLupNBqNR6IVhyvYvxKEAUZf6GpJNBqNxma04nAFGSshcTYERblaEo1Go7EZrTj6m5JsKMnURX8ajcZj0Yqjv8lYqZ614tBoNB6KWzQ5PKXIWAnx02HQUFdLotEMKFpaWigoKKCxsdHVongU/v7+xMfH4+PjY/VntOLoTyry4NguOPdPrpZEoxlwFBQUEBISQlJSEsI8eF7TI1JKysrKKCgoIDk52erPaVdVf5LxqXrWbiqNxuE0NjYSGRmplYYNCCGIjIy02UrTiqM/yfgUBk+ACOs1u0ajsR6tNGynL+dMK47+ovoYHNkCYxwxMFGj0Whch1Yc/UXmZ+pZV4trNJpuePHFF1m6dCkAr7/+OoWFhe3rbrvtNvbv3+8q0Tqhg+P9xf4VEDUKoke5WhKNRuOm3Hnnne2vX3/9dcaPH8/QoSoD87///a+rxDoJrTj6g7oyOPwDzL3P1ZJoNKcEf/x0H/sLqx26z7FDB/GHi8Z1uz4vL48FCxYwbdo0tm/fzrhx41i6dCmbNm3i/vvvp7W1lenTp/PCCy/g5+fHAw88wMqVK/H29ua8887j6aef5rHHHiM4OJikpCTS09O57rrrCAgIYNOmTSxcuJCnn36a9PR0Dhw4wN///ndAKZj09HT+85//8NZbb/Hcc8/R3NzMaaedxvPPP4+Xl5dDzwO4iatKCBEhhPhaCJFjeg63sE2iEGK7EGKnEGKfEOJOS/tyS7I+B2nU2VQazQAnKyuLu+66i4yMDAYNGsQzzzzDzTffzPvvv8+ePXtobW3lhRdeoKysjI8//ph9+/axe/dufv/733fazxVXXEFaWhpvv/02O3fuJCAgoH3d5Zdfzscff9z+/v333+fqq68mIyOD999/nx9++IGdO3fi5eXF22+/7ZS/010sjgeANVLKJ4UQD5je/67LNseAWVLKJiFEMLBXCLFSSlnYdWdux/6VEJYIgye6WhKN5pSgJ8vAmQwbNozZs2cDcP311/OnP/2J5ORkRo4cCcBNN93EkiVLuOeee/D39+enP/0pF154IRdeaH3D0+joaFJSUti8eTOpqalkZmYye/ZslixZwrZt25g+fToADQ0NxMTEOP6PxH0UxyJgnun1G8C3dFEcUsrmDm/9cBNrqVcaKuHgtzDzTtCpghrNgKZramtYWBhlZWUnbeft7c3WrVtZs2YNy5cv5z//+Q9r1661+jhXX301y5YtY/To0Vx66aUIIZBSctNNN/HXv/7V7r+jN9zl4hsrpTxmen0ciLW0kRBimBBiN3AE+Ft31oYQ4g4hRLoQIr2kpMQ5EltL9ldgbNFpuBrNKUB+fj6bNm0C4J133iEtLY28vDxyc3MBePPNNznzzDOpra2lqqqKCy64gH/+85/s2rXrpH2FhIRQU1Nj8TiXXnopK1as4N133+Xqq68G4JxzzmH58uUUFxcDUF5ezuHDh53xZ/afxSGE+AYYbGHVwx3fSCmlEEJa2oeU8ggwUQgxFPhECLFcSllkYbuXgZcB0tLSLO6r38hYCSFDIG6aS8XQaDTOZ9SoUSxZsoRbb72VsWPH8txzzzFz5kwWL17cHhy/8847KS8vZ9GiRTQ2NiKl5JlnnjlpXzfffDN33nlne3C8I+Hh4YwZM4b9+/czY8YMAMaOHcuf//xnzjvvPIxGIz4+PixZsoTExESH/51CStdeVwGEEFnAPCnlMSHEEOBbKWWPeatCiNeAVVLK5T1tl5aWJtPT0x0orQ0018FTw2HqDXDB310jg0ZzipCRkcGYMWNcdvy8vDwuvPBC9u7d6zIZ+oqlcyeE2CalTLO0vbu4qlYCN5le3wSs6LqBECJeCBFgeh0OzAGy+k3CvpDzNbQ2wBhd9KfRaAYO7qI4ngTOFULkAPNN7xFCpAkhzFUvY4AtQohdwHfA01LKPS6R1loyVkJgFCSe7mpJNBqNk0lKSvJIa6MvuEVWlZSyDDjHwvJ04DbT668Bz8lnbWlUgfHxl4PB8QU4Go1G4yrcxeIYeBz8FpprtZtKo9EMOLTicBYZK8EvFJLPcLUkGo1G41C04nAGbS2Q+TmMWgjevq6WRqPRaByKVhzOIO97aKzULdQ1Go3DqKys5Pnnn29/X1hYyBVXXOESWbTicAb7V4JPEAw/29WSaDSaAUJXxTF06FCWL++xjM1puEVW1YDC2KbcVKnngk9A79trNBrH88UDcNzB2fqDJ8DCJ7tdnZeXx8KFC5kzZw4bN24kLi6OFStWUFhYyN13301JSQmBgYG88sorjB49mgMHDnDddddRV1fHokWLePbZZ6mtraW2tpZFixZRUVFBS0sLf/7zn1m0aBEPPPAABw4cYPLkyZx77rncfffd7QWHM2fO5NVXX2XcONXccd68eTz99NOMGTOGX/ziF+zdu5eWlhYee+wxFi2yv/2RtjgcgdEIBdtgzePwwmyoK4axujeVRnOqkZOTw913382+ffsICwvjww8/5I477uDf//4327Zt4+mnn+auu+4C4Je//CW//OUv2bNnD/Hx8e378Pf35+OPP2b79u2sW7eO++67DyklTz75JMOHD2fnzp3tszjMXHXVVSxbtgyAY8eOcezYMdLS0njiiSc4++yz2bp1K+vWreM3v/kNdXV1dv+d2uLoK61NcGi9si6yvoDa4yC8VLHf9Kdh7CWullCjOXXpwTJwJsnJyUyePBmAadOmkZeXx8aNG1m8eHH7Nk1NTQBs2rSJTz75BIBrr72W+++/HwApJQ899BDr16/HYDBw9OhRiopOasnXiSuvvJLzzjuPP/7xjyxbtqw99rF69WpWrlzJ008/DUBjYyP5+fl2t2bRisMW6stVG5GszyF3jarT8AmCEefA6J9A6nkQGOFqKTUajYvw8/Nrf+3l5UVRURFhYWHs3LnT6n28/fbblJSUsG3bNnx8fEhKSqKxsbHHz8TFxREZGcnu3bt5//33efHFFwGlhD788ENGjXLsyGrtquqNijzY9Dy8fiH8fQR8fAfkb4YJV8C1H8BvD8JVb8Kkq7XS0Gg0nRg0aBDJycl88MEHgLqQm1uoz5w5kw8//BCA9957r/0zVVVVxMTE4OPjw7p169pbo/fUZh2Uu+qpp56iqqqKiRNVk43zzz+ff//735ib2e7YscMhf5dWHN1ReQSePx3+NQm+ehDqSmHOr+C2tXBvJlz0Lxh5Hvj4u1pSjUbjxrz99tu8+uqrTJo0iXHjxrFiherh+uyzz/LMM88wceJEcnNzCQ0NBeC6664jPT2dCRMmsHTpUkaPHg1AZGQks2fPZvz48fzmN7856ThXXHEF7733HldeeWX7skceeYSWlhYmTpzIuHHjeOSRRxzyN7lFW3Vn0ue26m2t8N61qvJ79AUQkeJ44TQajcNwdVt1W6mvrycgIAAhBO+99x7vvvtuu1Lpb2xtq65jHN3h5Q3XLXO1FBqNZoCybds27rnnHqSUhIWF8dprr7laJKvRikOj0WhcwNy5cy2OjPUEdIxDo9EMGAa6690Z9OWcacWh0WgGBP7+/pSVlWnlYQNSSsrKyvD3ty3JR7uqNBrNgCA+Pp6CggJKSkpcLYpH4e/v36ly3Rq04tBoNAMCHx8fkpOTXS3GKYF2VWk0Go3GJrTi0Gg0Go1NaMWh0Wg0GpsY8JXjQogS4LALDh0FlLrguO6MPicno8/JyehzcjKuOCeJUspoSysGvOJwFUKI9O7K9U9V9Dk5GX1OTkafk5Nxt3OiXVUajUajsQmtODQajUZjE1pxOI+XXS2AG6LPycnoc3Iy+pycjFudEx3j0Gg0Go1NaItDo9FoNDahFYdGo9FobEIrDgcghMgTQuwRQuwUQqSblkUIIb4WQuSYnsNdLaczEUK8JoQoFkLs7bDM4jkQiueEELlCiN1CiKmuk9x5dHNOHhNCHDV9V3YKIS7osO5B0znJEkKc7xqpnYsQYpgQYp0QYr8QYp8Q4pem5afsd6WHc+K+3xUppX7Y+QDygKguy54CHjC9fgD4m6vldPI5OAOYCuzt7RwAFwBfAAKYCWxxtfz9eE4eA+63sO1YYBfgByQDBwAvV/8NTjgnQ4CpptchQLbpbz9lvys9nBO3/a5oi8N5LALeML1+A7jEdaI4HynleqC8y+LuzsEiYKlUbAbChBBD+kXQfqSbc9Idi4D3pJRNUspDQC4ww2nCuQgp5TEp5XbT6xogA4jjFP6u9HBOusPl3xWtOByDBFYLIbYJIe4wLYuVUh4zvT4OxLpGNJfS3TmIA4502K6Ann8oA417TG6X1zq4ME+5cyKESAKmAFvQ3xXgpHMCbvpd0YrDMcyRUk4FFgJ3CyHO6LhSKvvylM571uegnReA4cBk4BjwD5dK4yKEEMHAh8CvpJTVHdedqt8VC+fEbb8rWnE4ACnlUdNzMfAxymwsMpvUpudi10noMro7B0eBYR22izctG/BIKYuklG1SSiPwCidcDKfMORFC+KAukG9LKT8yLT6lvyuWzok7f1e04rATIUSQECLE/Bo4D9gLrARuMm12E7DCNRK6lO7OwUrgRlPGzEygqoObYkDTxT9/Keq7AuqcXC2E8BNCJAOpwNb+ls/ZCCEE8CqQIaV8psOqU/a70t05cevviqszCjz9AaSgMhx2AfuAh03LI4E1QA7wDRDhalmdfB7eRZnTLSif60+7OweoDJklqGyQPUCaq+Xvx3Pypulv3o26AAzpsP3DpnOSBSx0tfxOOidzUG6o3cBO0+OCU/m70sM5cdvvim45otFoNBqb0K4qjUaj0diEVhwajUajsQmtODQajUZjE1pxaDQajcYmtOLQaDQajU1oxaHROBEhxM1CiFpXy6HROBKdjqvR9BEhRG8/njeAnwMhUnUV0GgGBN6uFkCj8WA6VvZeiGoL0XFZg5SyAWjoV6k0GiejXVUaTR+RUh43P4DKrsuklFVdXVWm4Tx7hRA3mQaA1Qkh/ieE8BVC3CWEOCKEKBNCPCOEMHT4nK8Q4m9CiAIhRL0Q4seBOuxJ4/5oi0Oj6X+SUDMVLkS1w/4QZakcQ/U6Gw0sA34wrQP4H6pT6rWo9iUXAJ8KIaZLKXf1p/AajVYcGk3/4wXcIqWsAvYKIb4EzgTipJTNQIYQ4gfgLOBDIcRw4BogSUqZb9rHf4QQ84GfAXf1/5+gOZXRikOj6X/yTUrDTBGQbVIaHZfFmF5PRTX7268aqbbjB6x1pqAajSW04tBo+p+WLu9lN8u8TK8NpvfTLWynA++afkcrDo3G/dmBsjgGSynXuVoYjUYrDo3GzZFSZgsh3gZeF0LcB2wHIoB5wEF5YoqeRtMvaMWh0XgGt6CG9zyFGhVajpr6pi0QTb+jK8c1Go1GYxO6AFCj0Wg0NqEVh0aj0WhsQisOjUaj0diEVhwajUajsQmtODQajUZjE1pxaDQajcYmtOLQaDQajU1oxaHRaDQam/h/RPD+dsNeeuoAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plt.plot(header,(values[values[:,0]>0]).mean(axis=0),label=\"positive\")\n",
"plt.plot(header,(values[values[:,0]<0]).mean(axis=0),label=\"negative\");\n",
"plt.xlabel(\"Time\",size=14)\n",
"plt.ylabel(\"Avg. Expression\",size=14)\n",
"plt.legend()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"outputs": [],
"source": []
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.9.6"
}
},
"nbformat": 4,
"nbformat_minor": 4
}
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Array Memory"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In the standard python interpretter, the return value of `id` is the memory address of the object."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"4448783488\n"
]
}
],
"source": [
"print(id(L))"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"-128\n"
]
}
],
"source": [
"print(id(L[1])-id(L[0])) #rows are far away"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"32\n"
]
}
],
"source": [
"print(id(L[0][1])-id(L[0][0])) #columns not so much, but 32 bytes?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Why does this matter?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
},
"tags": []
},
"source": [
"Keeping data close together results in faster access times.\n",
" * It's easier to figure out the location of the data\n",
" * The data is more likely to fit in the processor's *cache*"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"## If you have a *block* of *dense* numerical data, store it in a `numpy` array"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"source": [
"# Creating `numpy` Arrays"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note that `np.ndarray` and `np.array` are the same thing."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"dtype('int64')"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A = np.array([1,2,3,4])\n",
"A.dtype #type of what is stored in the array - NOT python types!"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"1"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A.ndim #number of dimensions (axes in numpy speak)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(4,)"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A.shape #size of the dimensions as a tuple"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(4, 1)"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A.reshape((4,1)).shape #a column vector"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"slideshow": {
"slide_type": "slide"
},
"tags": []
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"A = np.array([1,2,3,4]).reshape(4,1)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Initializing numpy Arrays"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"float64 (2, 3)\n"
]
}
],
"source": [
"#can initialize an array with a list, or list of lists (or list of lists of lists, etc)\n",
"M = np.array([[1,2,3],[4,5,6.0]])\n",
"print(M.dtype,M.shape)"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
"#if know the size, but not the data, can initialize to zeros:\n",
"Z = np.zeros((10,10))\n",
"#or ones\n",
"O = np.ones((5,10))\n",
"#or identity\n",
"I = np.identity(3) #this makes a 3x3 square identity matrix"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"float64\n"
]
}
],
"source": [
"print(Z.dtype) #note, default type is floating point"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"int64\n"
]
}
],
"source": [
"Z = np.zeros((10,10),np.int64) #can change\n",
"print(Z.dtype)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Indexing and Slicing"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"source": [
"`numpy` arrays can be indexed and sliced a lot like python lists, but take **tuples** of values to reference each dimension."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"outputs": [
{
"data": {
"text/plain": [
"array([[0, 1, 2],\n",
" [3, 4, 5]])"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"M = np.array([[0,1,2],[3,4,5]])\n",
"M"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"4\n",
"2\n"
]
}
],
"source": [
"print(M[1,1]) #indexing\n",
"print(M[0,-1]) #last item of first row"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[1 2]\n"
]
}
],
"source": [
"print(M[0,1:]) #can have slices - all but first column of first row"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[3 4 5] [3 4 5]\n"
]
}
],
"source": [
"print(M[1],M[1,:]) #missing indices are treated as complete slices"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"M = [[0,1,2],[3,4,5]]"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Advanced Slicing: Integer"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`numpy` arrays support advanced indexing by arrays of integers or booleans:"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [],
"source": [
"A = np.array([0,1,4,9,16,25])"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 4 25]\n"
]
}
],
"source": [
"print(A[[2,5]]) #choose just indices 2 and 5"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Advanced Slicing: Boolean\n",
"\n",
"Indexing by **Boolean** *numpy arrays* can be used to select elements"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[False False False True True True]\n"
]
}
],
"source": [
"b = A > 4\n",
"print(b)"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 9 16 25]\n"
]
}
],
"source": [
"print(A[b])"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Slicing Assignment"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"b = [False False False True True True]\n"
]
}
],
"source": [
"print(\"b =\",b)\n",
"A[b] = 0"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0 1 4 0 0 0]\n"
]
}
],
"source": [
"print(A)"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"S = np.array(['a','b','c','b','a'])\n",
"S[S != 'a'] = 'z'"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Array Views vs. Copies"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
" * A `numpy` array object has a pointer to a dense block of memory that stores the data of the array.\n",
" * *Basic* slices are just *views* of this data - they are **not** a new copy. \n",
" * Binding the same object to different variables will **not** create a copy.\n",
" * *Advanced* slices will create a copy if bound to a new variable - these are cases where the result may contain elements that are not contiguous in the original array "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Views"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [],
"source": [
"A = np.array([[0,1,2],[3,4,5],[6,7,8]])"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"True"
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"B = A #A and B reference the _same_ object\n",
"A is B"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[1000, 1, 2],\n",
" [ 3, 4, 5],\n",
" [ 6, 7, 8]])"
]
},
"execution_count": 36,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"B[0,0] = 1000\n",
"A"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Sliced Views"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([3, 4, 5])"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"row = A[1,:]\n",
"row"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[1000, 1, 2],\n",
" [ 3, 4, 5000],\n",
" [ 6, 7, 8]])"
]
},
"execution_count": 38,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"row[2] = 5000\n",
"A"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Explicit Copy"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[1000, 1, 2],\n",
" [ 3, 4, 5000],\n",
" [ 6, 7, 8]])"
]
},
"execution_count": 39,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"newMat = A.copy() #this will actually copy the data\n",
"newMat[0,0] = 0\n",
"A"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[ 0, 1, 2],\n",
" [ 3, 4, 5000],\n",
" [ 6, 7, 8]])"
]
},
"execution_count": 40,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"newMat"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Advanced Slices Copy"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([5, 6, 7, 8])"
]
},
"execution_count": 41,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A = np.array([[0,1,2],[3,4,5],[6,7,8]])\n",
"B = A[A > 4]\n",
"B"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([-1, -1, -1, -1])"
]
},
"execution_count": 42,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"B[:] = -1\n",
"B"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[0, 1, 2],\n",
" [3, 4, 5],\n",
" [6, 7, 8]])"
]
},
"execution_count": 43,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"but..."
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[ 0, 1, 2],\n",
" [ 3, 4, -1],\n",
" [-1, -1, -1]])"
]
},
"execution_count": 44,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A[A > 4] = -1\n",
"A"
]
},
{
"cell_type": "code",
"execution_count": 45,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"def z(M):\n",
" M[:] = 0\n",
"A = np.array([1,2,3])\n",
"z(A)"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Functions on Arrays\n",
"\n",
"`numpy` includes a number of standard functions that will work on arrays"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"2.5"
]
},
"execution_count": 47,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A = [1,2,3,4]\n",
"np.mean(A)"
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"10"
]
},
"execution_count": 48,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.sum(A)"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([ 0.84147098, 0.90929743, 0.14112001, -0.7568025 ])"
]
},
"execution_count": 49,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.sin(A)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Axis\n",
"\n",
"Most aggregation operations take an `axis` parameter that limits the operation to a specific direction in the array\n",
"* axis 0: across rows (apply operation to individual columns)\n",
"* axis 1: across columns (apply operation to individual rows)"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[ 0, 1, 2, 3],\n",
" [ 4, 5, 6, 7],\n",
" [ 8, 9, 10, 11]])"
]
},
"execution_count": 50,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b = np.arange(12).reshape(3,4); b"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"66"
]
},
"execution_count": 51,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.sum(b)"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([12, 15, 18, 21])"
]
},
"execution_count": 52,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.sum(b,axis=0)"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([ 6, 22, 38])"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.sum(b,axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Loading Data\n",
"\n",
"`genfromtxt` (and the simpler `loadtxt`) will read in deliminated files."
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([nan, nan, nan, ..., nan, nan, nan])"
]
},
"execution_count": 55,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.genfromtxt('../files/Spellman.csv')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The defaul delimiter is *whitespace* which will not work with a csv"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[ nan, 4.0000000e+01, 5.0000000e+01, ...,\n",
" 2.4000000e+02, 2.5000000e+02, 2.6000000e+02],\n",
" [ nan, -7.0000000e-02, -2.3000000e-01, ...,\n",
" 5.7000000e-01, 0.0000000e+00, 1.0000000e-02],\n",
" [ nan, 2.1500000e-01, 9.0000000e-02, ...,\n",
" -1.0000000e-01, 2.7000000e-01, 2.3500001e-01],\n",
" ...,\n",
" [ nan, -2.5500000e-01, -3.6000000e-01, ...,\n",
" 8.4000000e-01, -3.9000000e-01, -4.1500000e-01],\n",
" [ nan, 5.7000000e-01, 1.2000000e-01, ...,\n",
" -1.2000000e-01, 6.9000000e-01, 5.5500000e-01],\n",
" [ nan, 4.0500000e-01, 1.7000000e-01, ...,\n",
" -8.0000000e-02, 6.5000000e-01, 5.2000000e-01]])"
]
},
"execution_count": 56,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.genfromtxt('../files/Spellman.csv',delimiter=',')"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Why nan? "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Loading Data\n",
"\n",
"Recall that numpy arrays are dense, uniformly typed arrays. Can't mix a gene name (string) with expression values (float)."
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([['time', '40', '50', ..., '240', '250', '260'],\n",
" ['YAL001C', '-0.07', '-0.23', ..., '0.57', '0', '0.01'],\n",
" ['YAL014C', '0.215', '0.09', ..., '-0.1', '0.27', '0.23500001'],\n",
" ...,\n",
" ['YPR201W', '-0.255', '-0.36', ..., '0.84', '-0.39', '-0.415'],\n",
" ['YPR203W', '0.57', '0.12', ..., '-0.12', '0.69', '0.555'],\n",
" ['YPR204W', '0.405', '0.17', ..., '-0.08', '0.65', '0.52']],\n",
" dtype='\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%html\n",
"\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 61,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Help on function genfromtxt in module numpy:\n",
"\n",
"genfromtxt(fname, dtype=, comments='#', delimiter=None, skip_header=0, skip_footer=0, converters=None, missing_values=None, filling_values=None, usecols=None, names=None, excludelist=None, deletechars=\" !#$%&'()*+,-./:;<=>?@[\\\\]^{|}~\", replace_space='_', autostrip=False, case_sensitive=True, defaultfmt='f%i', unpack=None, usemask=False, loose=True, invalid_raise=True, max_rows=None, encoding='bytes', *, ndmin=0, like=None)\n",
" Load data from a text file, with missing values handled as specified.\n",
" \n",
" Each line past the first `skip_header` lines is split at the `delimiter`\n",
" character, and characters following the `comments` character are discarded.\n",
" \n",
" Parameters\n",
" ----------\n",
" fname : file, str, pathlib.Path, list of str, generator\n",
" File, filename, list, or generator to read. If the filename\n",
" extension is ``.gz`` or ``.bz2``, the file is first decompressed. Note\n",
" that generators must return bytes or strings. The strings\n",
" in a list or produced by a generator are treated as lines.\n",
" dtype : dtype, optional\n",
" Data type of the resulting array.\n",
" If None, the dtypes will be determined by the contents of each\n",
" column, individually.\n",
" comments : str, optional\n",
" The character used to indicate the start of a comment.\n",
" All the characters occurring on a line after a comment are discarded.\n",
" delimiter : str, int, or sequence, optional\n",
" The string used to separate values. By default, any consecutive\n",
" whitespaces act as delimiter. An integer or sequence of integers\n",
" can also be provided as width(s) of each field.\n",
" skiprows : int, optional\n",
" `skiprows` was removed in numpy 1.10. Please use `skip_header` instead.\n",
" skip_header : int, optional\n",
" The number of lines to skip at the beginning of the file.\n",
" skip_footer : int, optional\n",
" The number of lines to skip at the end of the file.\n",
" converters : variable, optional\n",
" The set of functions that convert the data of a column to a value.\n",
" The converters can also be used to provide a default value\n",
" for missing data: ``converters = {3: lambda s: float(s or 0)}``.\n",
" missing : variable, optional\n",
" `missing` was removed in numpy 1.10. Please use `missing_values`\n",
" instead.\n",
" missing_values : variable, optional\n",
" The set of strings corresponding to missing data.\n",
" filling_values : variable, optional\n",
" The set of values to be used as default when the data are missing.\n",
" usecols : sequence, optional\n",
" Which columns to read, with 0 being the first. For example,\n",
" ``usecols = (1, 4, 5)`` will extract the 2nd, 5th and 6th columns.\n",
" names : {None, True, str, sequence}, optional\n",
" If `names` is True, the field names are read from the first line after\n",
" the first `skip_header` lines. This line can optionally be preceded\n",
" by a comment delimiter. If `names` is a sequence or a single-string of\n",
" comma-separated names, the names will be used to define the field names\n",
" in a structured dtype. If `names` is None, the names of the dtype\n",
" fields will be used, if any.\n",
" excludelist : sequence, optional\n",
" A list of names to exclude. This list is appended to the default list\n",
" ['return','file','print']. Excluded names are appended with an\n",
" underscore: for example, `file` would become `file_`.\n",
" deletechars : str, optional\n",
" A string combining invalid characters that must be deleted from the\n",
" names.\n",
" defaultfmt : str, optional\n",
" A format used to define default field names, such as \"f%i\" or \"f_%02i\".\n",
" autostrip : bool, optional\n",
" Whether to automatically strip white spaces from the variables.\n",
" replace_space : char, optional\n",
" Character(s) used in replacement of white spaces in the variable\n",
" names. By default, use a '_'.\n",
" case_sensitive : {True, False, 'upper', 'lower'}, optional\n",
" If True, field names are case sensitive.\n",
" If False or 'upper', field names are converted to upper case.\n",
" If 'lower', field names are converted to lower case.\n",
" unpack : bool, optional\n",
" If True, the returned array is transposed, so that arguments may be\n",
" unpacked using ``x, y, z = genfromtxt(...)``. When used with a\n",
" structured data-type, arrays are returned for each field.\n",
" Default is False.\n",
" usemask : bool, optional\n",
" If True, return a masked array.\n",
" If False, return a regular array.\n",
" loose : bool, optional\n",
" If True, do not raise errors for invalid values.\n",
" invalid_raise : bool, optional\n",
" If True, an exception is raised if an inconsistency is detected in the\n",
" number of columns.\n",
" If False, a warning is emitted and the offending lines are skipped.\n",
" max_rows : int, optional\n",
" The maximum number of rows to read. Must not be used with skip_footer\n",
" at the same time. If given, the value must be at least 1. Default is\n",
" to read the entire file.\n",
" \n",
" .. versionadded:: 1.10.0\n",
" encoding : str, optional\n",
" Encoding used to decode the inputfile. Does not apply when `fname` is\n",
" a file object. The special value 'bytes' enables backward compatibility\n",
" workarounds that ensure that you receive byte arrays when possible\n",
" and passes latin1 encoded strings to converters. Override this value to\n",
" receive unicode arrays and pass strings as input to converters. If set\n",
" to None the system default is used. The default value is 'bytes'.\n",
" \n",
" .. versionadded:: 1.14.0\n",
" ndmin : int, optional\n",
" Same parameter as `loadtxt`\n",
" \n",
" .. versionadded:: 1.23.0\n",
" like : array_like, optional\n",
" Reference object to allow the creation of arrays which are not\n",
" NumPy arrays. If an array-like passed in as ``like`` supports\n",
" the ``__array_function__`` protocol, the result will be defined\n",
" by it. In this case, it ensures the creation of an array object\n",
" compatible with that passed in via this argument.\n",
" \n",
" .. versionadded:: 1.20.0\n",
" \n",
" Returns\n",
" -------\n",
" out : ndarray\n",
" Data read from the text file. If `usemask` is True, this is a\n",
" masked array.\n",
" \n",
" See Also\n",
" --------\n",
" numpy.loadtxt : equivalent function when no data is missing.\n",
" \n",
" Notes\n",
" -----\n",
" * When spaces are used as delimiters, or when no delimiter has been given\n",
" as input, there should not be any missing data between two fields.\n",
" * When the variables are named (either by a flexible dtype or with `names`),\n",
" there must not be any header in the file (else a ValueError\n",
" exception is raised).\n",
" * Individual values are not stripped of spaces by default.\n",
" When using a custom converter, make sure the function does remove spaces.\n",
" \n",
" References\n",
" ----------\n",
" .. [1] NumPy User Guide, section `I/O with NumPy\n",
" `_.\n",
" \n",
" Examples\n",
" --------\n",
" >>> from io import StringIO\n",
" >>> import numpy as np\n",
" \n",
" Comma delimited file with mixed dtype\n",
" \n",
" >>> s = StringIO(u\"1,1.3,abcde\")\n",
" >>> data = np.genfromtxt(s, dtype=[('myint','i8'),('myfloat','f8'),\n",
" ... ('mystring','S5')], delimiter=\",\")\n",
" >>> data\n",
" array((1, 1.3, b'abcde'),\n",
" dtype=[('myint', '>> _ = s.seek(0) # needed for StringIO example only\n",
" >>> data = np.genfromtxt(s, dtype=None,\n",
" ... names = ['myint','myfloat','mystring'], delimiter=\",\")\n",
" >>> data\n",
" array((1, 1.3, b'abcde'),\n",
" dtype=[('myint', '>> _ = s.seek(0)\n",
" >>> data = np.genfromtxt(s, dtype=\"i8,f8,S5\",\n",
" ... names=['myint','myfloat','mystring'], delimiter=\",\")\n",
" >>> data\n",
" array((1, 1.3, b'abcde'),\n",
" dtype=[('myint', '>> s = StringIO(u\"11.3abcde\")\n",
" >>> data = np.genfromtxt(s, dtype=None, names=['intvar','fltvar','strvar'],\n",
" ... delimiter=[1,3,5])\n",
" >>> data\n",
" array((1, 1.3, b'abcde'),\n",
" dtype=[('intvar', '>> f = StringIO('''\n",
" ... text,# of chars\n",
" ... hello world,11\n",
" ... numpy,5''')\n",
" >>> np.genfromtxt(f, dtype='S12,S12', delimiter=',')\n",
" array([(b'text', b''), (b'hello world', b'11'), (b'numpy', b'5')],\n",
" dtype=[('f0', 'S12'), ('f1', 'S12')])\n",
"\n"
]
}
],
"source": [
"help(np.genfromtxt)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Data Normalization\n",
"\n",
"## Q1: How would you rescale your data to range from 0 to 1?\n",
"\n",
"## Q2: How would you rescale your data to have zero mean and unit standard deviation?"
]
},
{
"cell_type": "code",
"execution_count": 62,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"array([[0.51995439, 0.50171038, 0.51653364, ..., 0.59293044, 0.52793615,\n",
" 0.5290764 ],\n",
" [0.55245154, 0.5381984 , 0.53078677, ..., 0.51653364, 0.55872292,\n",
" 0.55473204],\n",
" [0.54503991, 0.54503991, 0.55302166, ..., 0.48916762, 0.55644242,\n",
" 0.54960091],\n",
" ...,\n",
" [0.49885975, 0.48688712, 0.49372862, ..., 0.62371722, 0.48346636,\n",
" 0.48061574],\n",
" [0.59293044, 0.54161916, 0.51995439, ..., 0.51425314, 0.60661345,\n",
" 0.59122007],\n",
" [0.57411631, 0.54732041, 0.52280502, ..., 0.51881414, 0.60205245,\n",
" 0.58722919]])"
]
},
"execution_count": 62,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"(values-values.min())/(values.max()-values.min())"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"0.9999999999999999"
]
},
"execution_count": 63,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.std((values-values.mean())/values.std())"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Project: Expression Data\n",
"\n",
"https://MSCBIO2025.github.io/files/Spellman.csv\n",
"\n",
"* Read this data into a numpy array\n",
"* Plot a histogram of the expression values for the first time point\n",
"* Plot a histogram of the expression values for the last time point\n",
"* Plot a histogram of the average expression value for the genes across all time points\n",
"* Plot the average expression value (across all genes) at each time point as a line graph\n",
"* Plot two series of average expression values: one for all genes where the first value is positive and the other for all genes where the first value is negative\n"
]
},
{
"cell_type": "code",
"execution_count": 64,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD4CAYAAAAXUaZHAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAAAOWUlEQVR4nO3df6jd9X3H8edrzvlHLajkLktjXKRkg3R0sVys0P5hcZu/xqKjE/1DXedICxEUhBEVZmEIga5269iEdIoWnFZQMaxh0wbB9Q+tUcQfia6hjZgQTVo3FYSO6Ht/3K96TO/NPeeec+6593OfDzjc7/fz/XHe3+Tklc/9fH+cVBWSpLb8xqQLkCSNnuEuSQ0y3CWpQYa7JDXIcJekBv3mpAsAWLVqVa1fv37SZUjSsvLss8/+oqqmZlu2JMJ9/fr17NmzZ9JlSNKykuS1uZY5LCNJDTLcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ1aEneoSurf+m0//Gj6wPZLJ1iJljJ77pLUIMNdkhpkuEtSgxxzlxrkuLzsuUtSgwx3SWqQwzJSI3qHYiR77pLUIMNdkhpkuEtSgxxzl5Yxx9k1l3l77knWJXkiyd4kLye5oWv/ZpJDSZ7vXpf0bHNzkv1JXk1y4TgPQNKJrd/2w49eWjn66bkfA26qqueSfBp4Nsnj3bLvVNXf966cZCNwJfA54DPAj5L8XlW9P8rCJUlzm7fnXlWHq+q5bvpdYB+w9gSbbAYeqKpfVdXPgf3AuaMoVpLUn4FOqCZZD5wDPN01XZ/khSR3Jzm9a1sLvN6z2UFm+c8gyZYke5LsOXr06OCVS5Lm1He4JzkVeAi4sareAe4EPgtsAg4D3x7kjatqR1VNV9X01NTUIJtKkubRV7gnOZmZYL+vqh4GqKo3q+r9qvoA+B4fD70cAtb1bH5m1yZJWiT9XC0T4C5gX1Xd0dO+pme1y4GXuumdwJVJTklyNrAB+MnoSpYkzaefq2W+BFwNvJjk+a7tFuCqJJuAAg4AXweoqpeTPAjsZeZKm61eKSNJi2vecK+qHwOZZdGuE2xzO3D7EHVJkobg4wckqUGGuyQ1yHCXpAYZ7pLUIMNdkhpkuEtSg3yeu7RE9T6i98D2SydYiZYje+6S1CDDXZIa5LCMtAz4LUoalD13SWqQ4S5JDTLcJalBjrlLK5SXWrbNnrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkNmjfck6xL8kSSvUleTnJD135GkseT/LT7eXrXniTfTbI/yQtJvjDug5AkfVI/PfdjwE1VtRE4D9iaZCOwDdhdVRuA3d08wMXAhu61Bbhz5FVLkk5o3nCvqsNV9Vw3/S6wD1gLbAbu7Va7F7ism94MfL9mPAWclmTNqAuXJM1toK/ZS7IeOAd4GlhdVYe7RW8Aq7vptcDrPZsd7NoO97SRZAszPXvOOuusQeuWtAC9X62ntvV9QjXJqcBDwI1V9U7vsqoqoAZ546raUVXTVTU9NTU1yKaSpHn0Fe5JTmYm2O+rqoe75jc/HG7pfh7p2g8B63o2P7NrkyQtkn6ulglwF7Cvqu7oWbQTuLabvhZ4tKf9mu6qmfOAt3uGbyRJi6CfMfcvAVcDLyZ5vmu7BdgOPJjkOuA14Ipu2S7gEmA/8B7wtVEWLEma37zhXlU/BjLH4gtmWb+ArUPWJUkagneoSlKDDHdJapDhLkkNMtwlqUGGuyQ1yHCXpAYZ7pLUoIEeHCZpvHywl0bFnrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkNMtwlqUGGuyQ1yG9ikvSJb4A6sP3SCVaiUbHnLkkNMtwlqUGGuyQ1yHCXpAbNG+5J7k5yJMlLPW3fTHIoyfPd65KeZTcn2Z/k1SQXjqtwSdLc+um53wNcNEv7d6pqU/faBZBkI3Al8Llum39JctKoipUk9WfecK+qJ4G3+tzfZuCBqvpVVf0c2A+cO0R9kqQFGGbM/fokL3TDNqd3bWuB13vWOdi1/ZokW5LsSbLn6NGjQ5QhSTreQsP9TuCzwCbgMPDtQXdQVTuqarqqpqemphZYhiRpNgsK96p6s6rer6oPgO/x8dDLIWBdz6pndm2SpEW0oHBPsqZn9nLgwytpdgJXJjklydnABuAnw5UoSRrUvM+WSXI/cD6wKslB4Dbg/CSbgAIOAF8HqKqXkzwI7AWOAVur6v2xVC5JmtO84V5VV83SfNcJ1r8duH2YoiRJw/EOVUlqkI/8lSbAR+xq3Oy5S1KD7LlL+oTe3yrA3yyWK3vuktQge+7ShB3fU5ZGwZ67JDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkNMtwlqUHexCTphHzI2fJkz12SGmS4S1KDHJaRFonPkNFisucuSQ0y3CWpQYa7JDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkNMtwlqUGGuyQ1aN5wT3J3kiNJXuppOyPJ40l+2v08vWtPku8m2Z/khSRfGGfxkqTZ9dNzvwe46Li2bcDuqtoA7O7mAS4GNnSvLcCdoylTkjSIecO9qp4E3jqueTNwbzd9L3BZT/v3a8ZTwGlJ1oyoVklSnxY65r66qg53028Aq7vptcDrPesd7Np+TZItSfYk2XP06NEFliFJms3QJ1SrqoBawHY7qmq6qqanpqaGLUOS1GOhX9bxZpI1VXW4G3Y50rUfAtb1rHdm1yatSH5BhyZloT33ncC13fS1wKM97dd0V82cB7zdM3wjSVok8/bck9wPnA+sSnIQuA3YDjyY5DrgNeCKbvVdwCXAfuA94GtjqFmSNI95w72qrppj0QWzrFvA1mGLkiQNxztUJalBhrskNchwl6QGGe6S1KCFXucuaQ5e266lwJ67JDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkN8jp3SQvSez3/ge2XTrASzcZwl9Q3b9BaPhyWkaQGGe6S1CDDXZIa5Ji7NAKORWupsecuSQ0y3CWpQYa7JDXIcJekBhnuktQgw12SGuSlkNICefmjljJ77pLUIHvukobmEyKXHnvuktQge+6SRspe/NIwVLgnOQC8C7wPHKuq6SRnAD8A1gMHgCuq6n+GK1OSNIhRDMt8pao2VdV0N78N2F1VG4Dd3bwkaRGNY8x9M3BvN30vcNkY3kOSdALDhnsBjyV5NsmWrm11VR3upt8AVs+2YZItSfYk2XP06NEhy5Ak9Rr2hOqXq+pQkt8GHk/ySu/CqqokNduGVbUD2AEwPT096zrSUuONS1ouhuq5V9Wh7ucR4BHgXODNJGsAup9Hhi1SkjSYBYd7kk8l+fSH08CfAC8BO4Fru9WuBR4dtkhJ0mCGGZZZDTyS5MP9/FtV/UeSZ4AHk1wHvAZcMXyZ0uQ4FKPlaMHhXlU/A/5wlvZfAhcMU5QkaTg+fkCSGmS4S1KDfLaMNAvH2bXcGe6SxsaHiE2OwzKS1CDDXZIa5LCMpEXhEM3isucuSQ0y3CWpQYa7JDXIcJekBnlCVSuWNyqpZYa7VhQDXSuFwzKS1CB77pIW3VzXvHst/OjYc5ekBtlzlzRRngcZD3vuktQge+6SljzH4gdnz12SGmS4S1KDHJZR8zxhp5XIcFeTDHStdIa7mmGgt6Wfv09PtM7NcNeS4p2L0mh4QlWSGmTPXdKy4vBbfwx3LZq5/lHONcwy1/oO0Wg2fi4+yXDXvJbyOLi9OM1nKXxOJ8Fw18QZ0NLojS3ck1wE/CNwEvCvVbV9XO+1EixG76Of9xj08jRpKRn0M36if2tL/TeCsYR7kpOAfwb+GDgIPJNkZ1XtHcf7tWpcITmqEJeWqkE/vy12WsbVcz8X2F9VPwNI8gCwGRh5uJ/oD3yY/00HPfk37v30s/+F7HNUH9jl9sGXFqPz1I9x9fpTVaPfafJV4KKq+utu/mrgi1V1fc86W4At3ezvA6+OvJDBrAJ+MeEaFoPH2ZaVcpywco51kOP83aqamm3BxE6oVtUOYMek3v94SfZU1fSk6xg3j7MtK+U4YeUc66iOc1x3qB4C1vXMn9m1SZIWwbjC/RlgQ5Kzk/wWcCWwc0zvJUk6zliGZarqWJLrgf9k5lLIu6vq5XG81wgtmSGiMfM427JSjhNWzrGO5DjHckJVkjRZPhVSkhpkuEtSgwz3TpK/S/JCkueTPJbkM5OuaVySfCvJK93xPpLktEnXNA5J/iLJy0k+SNLcJXRJLkryapL9SbZNup5xSXJ3kiNJXpp0LeOSZF2SJ5Ls7T6zNwy7T8P9Y9+qqs9X1Sbg34G/nXA94/Q48AdV9Xngv4GbJ1zPuLwE/Dnw5KQLGbWeR3xcDGwErkqycbJVjc09wEWTLmLMjgE3VdVG4Dxg67B/n4Z7p6re6Zn9FNDsmeaqeqyqjnWzTzFzH0JzqmpfVU36zudx+egRH1X1f8CHj/hoTlU9Cbw16TrGqaoOV9Vz3fS7wD5g7TD79JG/PZLcDlwDvA18ZcLlLJa/An4w6SI0sLXA6z3zB4EvTqgWjVCS9cA5wNPD7GdFhXuSHwG/M8uiW6vq0aq6Fbg1yc3A9cBti1rgCM13rN06tzLz6+B9i1nbKPVznNJykeRU4CHgxuNGEwa2osK9qv6oz1XvA3axjMN9vmNN8pfAnwIX1DK+2WGAv9PW+IiPxiQ5mZlgv6+qHh52f465d5Js6JndDLwyqVrGrfsilb8B/qyq3pt0PVoQH/HRkCQB7gL2VdUdI9nnMu60jVSSh5h59PAHwGvAN6qqyZ5Qkv3AKcAvu6anquobEyxpLJJcDvwTMAX8L/B8VV040aJGKMklwD/w8SM+bp9sReOR5H7gfGYehfsmcFtV3TXRokYsyZeB/wJeZCaDAG6pql0L3qfhLkntcVhGkhpkuEtSgwx3SWqQ4S5JDTLcJalBhrskNchwl6QG/T/f+Nm+J6yvwAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"#bins = [-3,-2,-1,0,1,2,3]\n",
"#bins = np.linspace(-3,3,100)\n",
"plt.hist(values[:,0],bins=100);"
]
},
{
"cell_type": "code",
"execution_count": 65,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD4CAYAAAAXUaZHAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAAANx0lEQVR4nO3df+hd9X3H8edrzvWPKaiYZS6GRUpWSMcWyxfn6P5wc1v9MRYdm+gfNusc6R8RFISh7R/tP4XAVsvKNkc6xRScTlAxrHZtGgQpTOs3Emxi6hraiAnRfDtHFYSO2Pf+yIm7xm/y/XF/nO/3c58PuNxzPuece9+HfO/rfvI5P26qCklSW36h7wIkSaNnuEtSgwx3SWqQ4S5JDTLcJalBv9h3AQCXXnppbdiwoe8yJGlV2bdv30+qas18y1ZEuG/YsIHZ2dm+y5CkVSXJa2db5rCMJDXIcJekBhnuktQgw12SGmS4S1KDDHdJapDhLkkNMtwlqUGGuyQ1aEVcoSqN2oZ7v/H+9JEdN/ZYidQPe+6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXI89zVjMFz26VpZ89dkhq0YLgnWZ/k2SSvJDmY5K6u/YtJjiXZ3z1uGNjmviSHk7ya5FPj3AFJ0octZljmJHBPVb2U5EJgX5I93bKvVNXfDa6cZBNwK/Bx4NeA7yT5jap6b5SFS5LObsGee1Udr6qXuul3gEPAunNssgV4rKp+VlU/Bg4DV42iWEnS4ixpzD3JBuBK4IWu6c4kLyd5KMnFXds64PWBzY5y7i8DSdKILTrck1wAPAHcXVVvAw8AHwU2A8eBLy/ljZNsSzKbZHZubm4pm0qSFrCoUyGTnM+pYH+kqp4EqKo3B5Z/Dfj3bvYYsH5g88u7tg+oqp3AToCZmZlaTvHSUnkrYE2LxZwtE+BB4FBV3T/QftnAajcDB7rp3cCtST6S5ApgI/C90ZUsSVrIYnrunwRuB76fZH/X9jngtiSbgQKOAJ8FqKqDSR4HXuHUmTbbPVNGkiZrwXCvqu8CmWfRM+fY5kvAl4aoS5I0BK9QlaQGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIn9nTquZP60nzs+cuSQ0y3CWpQYa7JDXIcJekBnlAVVPrzIOx/niHWmK4q3meUaNpZLhr1TGspYU55i5JDTLcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIe8tIncF71niHSK129twlqUGGuyQ1aMFwT7I+ybNJXklyMMldXfslSfYk+WH3fHHXniRfTXI4yctJPjHunZAkfdBieu4ngXuqahNwNbA9ySbgXmBvVW0E9nbzANcDG7vHNuCBkVctSTqnBcO9qo5X1Uvd9DvAIWAdsAXY1a22C7ipm94CfL1OeR64KMlloy5cknR2SxpzT7IBuBJ4AVhbVce7RW8Aa7vpdcDrA5sd7drOfK1tSWaTzM7NzS21bknSOSw63JNcADwB3F1Vbw8uq6oCailvXFU7q2qmqmbWrFmzlE0lSQtYVLgnOZ9Twf5IVT3ZNb95erilez7RtR8D1g9sfnnXJkmakMWcLRPgQeBQVd0/sGg3sLWb3go8PdD+6e6smauBnw4M30iSJmAxV6h+Ergd+H6S/V3b54AdwONJ7gBeA27plj0D3AAcBt4FPjPKgiVJC1sw3Kvqu0DOsvjaedYvYPuQdUkfMHhrAEkL8wpVSWqQ4S5JDTLcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIcJekBhnuktQgw12SGmS4S1KDDHdJatBifmZP6sVK+fWlwTqO7Lixx0qkxbPnLkkNMtwlqUGGuyQ1yDF3aR4rZbxfWi7DXSuKoSqNhsMyktQgw12SGmS4S1KDDHdJapDhLkkN8mwZaQm8FYFWC3vuktSgBcM9yUNJTiQ5MND2xSTHkuzvHjcMLLsvyeEkryb51LgKlySd3WJ67g8D183T/pWq2tw9ngFIsgm4Ffh4t80/JTlvVMVKkhZnwXCvqueAtxb5eluAx6rqZ1X1Y+AwcNUQ9UmSlmGYMfc7k7zcDdtc3LWtA14fWOdo1/YhSbYlmU0yOzc3N0QZkqQzLTfcHwA+CmwGjgNfXuoLVNXOqpqpqpk1a9YsswxJ0nyWFe5V9WZVvVdVPwe+xv8PvRwD1g+sennXJkmaoGWFe5LLBmZvBk6fSbMbuDXJR5JcAWwEvjdciZKkpVrwIqYkjwLXAJcmOQp8AbgmyWaggCPAZwGq6mCSx4FXgJPA9qp6byyVS5LOKlXVdw3MzMzU7Oxs32VoBVit93P3alX1Icm+qpqZb5lXqEpSgwx3SWqQ4S5JDTLcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoP8DVX1brVelSqtZPbcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQV6hql54Vao0XvbcJalBhrskNchwl6QGGe6S1CDDXZIaZLhLUoM8FVIagcFTO4/suLHHSqRT7LlLUoMMd0lq0ILhnuShJCeSHBhouyTJniQ/7J4v7tqT5KtJDid5Ocknxlm8JGl+i+m5Pwxcd0bbvcDeqtoI7O3mAa4HNnaPbcADoylTkrQUC4Z7VT0HvHVG8xZgVze9C7hpoP3rdcrzwEVJLhtRrZKkRVrumPvaqjreTb8BrO2m1wGvD6x3tGuTJE3Q0AdUq6qAWup2SbYlmU0yOzc3N2wZkqQByw33N08Pt3TPJ7r2Y8D6gfUu79o+pKp2VtVMVc2sWbNmmWVIkuaz3HDfDWztprcCTw+0f7o7a+Zq4KcDwzeSpAlZ8ArVJI8C1wCXJjkKfAHYATye5A7gNeCWbvVngBuAw8C7wGfGULNWEa/clPqxYLhX1W1nWXTtPOsWsH3YoiRJw/EKVUlqkOEuSQ0y3CWpQd7yVxojDyirL/bcJalBhrskNchhGU3M4BCFpPGy5y5JDTLcJalBhrskNchwl6QGGe6S1CDPlpFGzLOCtBLYc5ekBhnuktQgh2WkCfE+M5oke+6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQYa7JDXIcJekBhnuktQgr1CVeuDVqho3e+6S1CDDXZIaZLhLUoMcc9fI+WMVUv+GCvckR4B3gPeAk1U1k+QS4N+ADcAR4Jaq+p/hypQkLcUohmV+v6o2V9VMN38vsLeqNgJ7u3lJ0gSNY8x9C7Crm94F3DSG95AkncOw4V7At5PsS7Kta1tbVce76TeAtfNtmGRbktkks3Nzc0OWIUkaNOwB1d+rqmNJfgXYk+QHgwurqpLUfBtW1U5gJ8DMzMy860iSlmeonntVHeueTwBPAVcBbya5DKB7PjFskZKkpVl2uCf55SQXnp4G/hg4AOwGtnarbQWeHrZISdLSDDMssxZ4Ksnp1/nXqvqPJC8Cjye5A3gNuGX4MiVJS7HscK+qHwG/PU/7fwPXDlOUJGk4XqGqkfCqVGll8d4yktQge+5Sz7y3u8bBnrskNcieu7RC2aPXMOy5S1KDDHdJapDDMtIq4BCNlsqeuyQ1yJ67ls0Ll6SVy3CXVhC/MDUqDstIUoPsuWtJ7FlKq4PhLq0ynjmjxXBYRpIaZLhLUoMMd0lqkGPuWpAHUVcfx+Vlz12SGmS4S1KDDHdJapDhLkkN8oCq1AgPfGuQPXdJapA9d2kVs7eus7HnLkkNsueuedkjbIcXNE0nw33K+cHXmc78YvfvYnUy3PU+e+vt88t8ehju0pSaRND7ZdKfsYV7kuuAvwfOA/6lqnaM672mzVI/MPbItZBz/Y2cbdng354hvvKMJdyTnAf8I/BHwFHgxSS7q+qVcbzfNPNDpdViMV8Sw7ymf/8fNK6e+1XA4ar6EUCSx4AtwMjD/Vw9jnH8Yw/Tax7H+lJfzvbZW+r/FJe6/jCfo5UyFDWJOlJVo3/R5M+B66rqr7v524Hfqao7B9bZBmzrZj8GvDryQhbnUuAnPb13n9zv6TOt+97yfv96Va2Zb0FvB1Sraiews6/3Py3JbFXN9F3HpLnf02da931a93tcV6geA9YPzF/etUmSJmBc4f4isDHJFUl+CbgV2D2m95IknWEswzJVdTLJncC3OHUq5ENVdXAc7zUCvQ8N9cT9nj7Tuu9Tud9jOaAqSeqXd4WUpAYZ7pLUIMMdSPK3SX6Q5OUkTyW5qO+aJiHJXyQ5mOTnSZo/VSzJdUleTXI4yb191zMpSR5KciLJgb5rmaQk65M8m+SV7u/8rr5rmiTD/ZQ9wG9W1W8B/wXc13M9k3IA+DPgub4LGbeBW2JcD2wCbkuyqd+qJuZh4Lq+i+jBSeCeqtoEXA1sn6J/c8MdoKq+XVUnu9nnOXVefvOq6lBV9XVl8KS9f0uMqvpf4PQtMZpXVc8Bb/Vdx6RV1fGqeqmbfgc4BKzrt6rJMdw/7K+Ab/ZdhEZuHfD6wPxRpuiDPu2SbACuBF7ouZSJmZr7uSf5DvCr8yz6fFU93a3zeU79V+6RSdY2TovZb6llSS4AngDurqq3+65nUqYm3KvqD8+1PMlfAn8CXFsNnfy/0H5PEW+JMYWSnM+pYH+kqp7su55JcliG939Y5G+AP62qd/uuR2PhLTGmTJIADwKHqur+vuuZNMP9lH8ALgT2JNmf5J/7LmgSktyc5Cjwu8A3knyr75rGpTtgfvqWGIeAx1fwLTFGKsmjwH8CH0tyNMkdfdc0IZ8Ebgf+oPtc709yQ99FTYq3H5CkBtlzl6QGGe6S1CDDXZIaZLhLUoMMd0lqkOEuSQ0y3CWpQf8HJXuJ/flNKXMAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plt.hist(values[:,-1],bins=100);"
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"Text(0, 0.5, 'Number of Instances')"
]
},
"execution_count": 66,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYkAAAEKCAYAAADn+anLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAAAik0lEQVR4nO3de5xVdb3/8dcbRSkhMUAPchEUPYqWo42GWV7z2knFNPV0UPNC55ecvORRzNNPsviJx5LqeDJJNOio6NEMKy2RUOvxEA0Jb5A6ouAQecHwloCDn98fa824GfeeWTOz96w9e97Px2M/Zq/vWnutz+KyP7O+37U+X0UEZmZmxfTJOwAzM6teThJmZlaSk4SZmZXkJGFmZiU5SZiZWUmb5x1AOQ0ePDhGjRqVdxhmZj3Ko48++mpEDCm2rqaSxKhRo1i0aFHeYZiZ9SiSVpRa5+4mMzMryUnCzMxKcpIwM7OSampMwsystXfffZfGxkbWrVuXdyi569evH8OHD6dv376ZP+MkYWY1rbGxkQEDBjBq1Cgk5R1ObiKCNWvW0NjYyOjRozN/zt1NZlbT1q1bx6BBg3p1ggCQxKBBgzp8ReUkYWY1r7cniGad+XNwkjAzs5I8JmFmvcr0ec+UdX/nH7ZLm+vXrl3LzTffzFe/+tUO7XflypWMHTuWKVOmcOGFFwLwm9/8hnPPPZeNGzdy1llnMXny5E7HnZWvJMwqbPq8Z1pe1vusXbuWH/3oRx3+3AUXXMBRRx3Vsrxx40bOOecc7rnnHpYuXcott9zC0qVLyxlqUb6SMDOroMmTJ/Pcc89RV1fHPvvsw9NPP80bb7xBU1MT1157LZ/5zGc+8Jlf/OIXjB49mq222qql7ZFHHmHMmDHsuOOOAJx88snMnTuXsWPHVjR+X0mYmVXQtGnT2GmnnViyZAm77rorRxxxBEuWLOGxxx6jrq7uA9u/9dZbXHnllVx22WWbtK9atYoRI0a0LA8fPpxVq1ZVOnxfSZiZdZd99tmHM844g3fffZfjjjuuaJKYMmUK559/Pv379+/+AItwkjAz6yYHHHAADz74IL/+9a85/fTTueCCCxgwYADf+ta3ALj++ut5+OGHuf3227noootYu3Ytffr0oV+/fnziE5/gxRdfbNlXY2Mjw4YNq3jMThJmZhU0YMAA3nzzTQBWrFjB8OHDOfvss1m/fj2LFy/m+9//PuPHj2/Z/ve//33L+ylTptC/f38mTZpEU1MTzz77LM8//zzDhg1jzpw53HzzzRWP30nCzHqV9m5ZLbdBgwax//77s8cee/D222+z1VZb0bdvX/r378/s2bMz72fzzTfnmmuu4YgjjmDjxo2cccYZ7L777hWMPD1uxY9gZtbLdfY3/ilTpmyyfPTRR3P00UeXIaLsfHeTmZmV5CRhZmYlOUmYmVlJThJmZlaSk4SZmZXkJGFmZiV12y2wkvoBDwJbpse9PSIukzQamAMMAh4FJkTEBklbArOBTwBrgJMi4oXuitfMatSCK8q7v4MvaXN1R0uFz5s3j8mTJ7Nhwwa22GILrrrqKg455BAANmzYwKRJk7j//vvp06cPU6dO5Qtf+ALr16/n1FNP5dFHH2XQoEHceuutjBo1qqtnBnTvlcR64JCI2BOoA46UNA64EpgeEWOAvwFnptufCfwtbZ+ebmdWM1xCvHfoaKnwwYMH88tf/pInnniCWbNmMWHChJZ1U6dOZdttt+WZZ55h6dKlHHjggQDMnDmTbbbZhoaGBs4//3wuvvjissXfbUkiEm+li33TVwCHALen7bOA49L3x6bLpOsPlecgNLMeprBU+Nlnn80BBxxAXV0de+yxxyYlOJrttddebL/99gDsvvvuvPPOO6xfvx6AG264gUsuSa5c+vTpw+DBgwGYO3cup512GgAnnHAC8+fPJyLKEn+3jklI2kzSEuBlYB7wHLA2IprSTRqB5opVw4AXAdL1r5N0SbXe50RJiyQteuWVVyp8BmZmHdPRUuGF7rjjDvbee2+23HJL1q5dC8A3v/lN9t57b0488UReeuklYNMy4ptvvjlbb701a9asKUv83ZokImJjRNQBw4F9gV3LsM8ZEVEfEfVDhgzp6u7MzCpmn3324cYbb2TKlCk88cQTDBgwoOS2Tz31FBdffDHXXXcdAE1NTTQ2NvKpT32KxYsXs99++7VMa1pJudzdFBFrgQXAfsBASc0D6MOB5lk0VgEjANL1W5MMYJv1WB6H6N2aS4UPGzaM008/ndmzZ3PnnXdSV1dHXV0dixYtApIy4OPHj2f27NnstNNOQFIo8MMf/jDHH388ACeeeCKLFy8GYNiwYS1lxJuamnj99dcZNOgDHS+d0m1JQtIQSQPT9x8CDgOWkSSLE9LNTgPmpu/vSpdJ1/8uytXJZmbWTVqXCt9uu+04++yzOeuss1i8eDHjx49nyZIlLFmyhPr6etauXcvnPvc5pk2bxv7779+yH0l8/vOf5/777wdg/vz5LVOXHnPMMcyalQzh3n777RxyyCGUawi3O6vADgVmSdqMJDndFhG/krQUmCPpO8CfgJnp9jOBn0lqAF4DTu7GWM2sVrVzy2q5dbRU+DXXXENDQwOXX345l19+OQD33nsv2267LVdeeSUTJkzgvPPOY8iQIdx4440AnHnmmUyYMIExY8bw0Y9+lDlz5pQtftXSL+f19fXRfLlmlqeOdid19xwHvcmyZcvYbbfd8g6jahT785D0aETUF9veT1ybmVlJThJmZlaSk4SZ1bxa6lbvis78OThJmFlN69evH2vWrOn1iSIiWLNmDf369evQ5zp9d5OkMUBjRKzr7D7MzCpt+PDhNDY24ooMScIcPnx4hz6TKUlI+n/A0xExK62fdC9wKPC6pCMj4uEOR2tm1g369u3L6NGj8w6jx8p6JfEl4KT0/VEkVVzHpe3TgIPLHplZL1J4y6xvh7VqkjVJbEdSfA/gaJIH4R6R9BrgBxPMzGpU1oHrNcAO6fvDgfnp+80Bl+82M6tRWa8k7gBulvQM8FHgt2l7HdBQgbjMzKwKZE0SFwArgJHARRHxdto+FLi2EoGZmVn+MiWJdNKf7xVpn172iMzMrGpkfphO0sckXSPpHklD07bjJO1VufDMzCxPmZKEpMOBP5JMKXoI8KF01U7AZZUJzczM8pb1SuLbwAURMR7YUNB+P8k0pGZmVoOyJok9gLuLtL9GcreTmRUYt3IG41bOyDsMsy7LmiReI+lqam1v3n/IzszMakzWJHEzcJWk4UAAm0s6EPgu8MH598zMrCZkTRL/ATxP8qxEf2Ap8DvgD8DUyoRmZmZ5y/qcxLvAlyR9k6SLqQ/wp4h4tpLBmZlZvrKWCt8C6BMRy4HlBe39gPciYkPJD5uZWY+VtSzH/wIPAFe3av9X4CDguPKFZNYzFZb7HpdjHGbllDVJ7A9cWqR9HvCN8oVj1nP5llerRVkHrj8MNBVpfw8YkGUHkkZIWiBpqaSnJJ2btk+RtErSkvR1dMFnLpHUIOlpSUdkjNXMzMok65XE48ApfLAExz8DT2bcRxPw9YhYLGkA8Kikeem66RHx3cKNJY0FTgZ2B7YH7pO0S0RszHg8MzProqxJ4nJgrqQxJLe+QjLH9YnA+Cw7iIjVwOr0/ZuSllH8Ab1mxwJzImI98LykBpISIA9ljNnMzLooU3dTRNwNfJ5kdrofpq+RwDER8auOHlTSKGAv4OG0aZKkxyXdIGmbtG0Y8GLBxxopklQkTZS0SNKiV155paOhmJlZGzKXCo+I30TEpyNiq/T16Yi4p6MHlNSfZKa78yLiDZJJi3YimeVuNUXmrWgnrhkRUR8R9UOGDOloOGbdxvWcrCfK2t3UQtJAWiWXiHgt42f7kiSImyLi5+lnXypY/xOg+cpkFTCi4OPD0zazmlZ4K+35h+2SYyRm2eeT2CGdbOgdYA3wSvp6Nf2ZZR8CZgLLIuLqgvahBZuN5/2B8LuAkyVtKWk0sDPwSJZjmZlZeWS9krgRGAicCfyFpMhfR+0PTACekLQkbfsGcIqkunSfLwBfAYiIpyTdRlInqgk4x3c2mZl1r6xJYl9gXERkvd31AyLiD4CKrCo2T0XzZ6biAoJmZrnJOnD9PLBlJQMxM7PqkzVJnAtckT4nYWZmvUTW7qa5JFcST0taT6sSHRHxkXIHZmZm+cuaJCZVNAozM6tKWScdmlXpQMzMrPp05mG6fwC2KGyLiJVli8isp1lwRd4RmFVM1pnptiap1/RFWiWI1GblDMrMzKpD1rubvgvsSTID3TqSEuH/TlJ076SKRGZmZrnL2t10FHBKRPxe0kbg0Yi4VdJqkiekb69YhGZmlpusSWIgsCJ9/zowCGggmdvh+vKHZVa7CivBLhw5McdIzNqXNUk8B+wIrASWkRTeewQ4HshUAdasN3JpcOvpsiaJnwIfB+4HppGU855EMqZxbiUCM6tqvqPJeomsz0lML3j/O0m7AvXAsxHxRKWCMzOzfGW9BfZU4NZ0vunm5yJWStpC0qkRMbuSQZpVq4eWr8k7BLOKynoL7I3A1kXaB6TrzMysBmVNEqL4REMjSe52MjOzGtRmd5OkJ0iSQwAPSCqs/roZsANtTBpkZmY9W3tjEs0Pye0B/Bp4q2DdBpLpRu8of1hmBjB93jObLJ9/2C45RWK9VZtJIiK+BSDpBWBO88C1mZn1DlnHJO4GWiYWkvQxSd+RdEplwjIzs2qQNUncBnweQNJg4EFgPPBjSV+vUGxmNW/cyhl+KtuqWtYk8XFgYfr+BKAhInYHTiUp8GdmZjUoa5L4EO8PWn8WuCt9vxgYkWUHkkZIWiBpqaSnJJ2btn9U0jxJz6Y/t0nbJemHkhokPS5p7+ynZWZm5ZA1STwLHC9pBHA4cG/avh2wNuM+moCvR8RYYBxwjqSxwGRgfkTsDMxPlyEpT75z+poIXJvxOGZmViZZk8S3gCtJbnldGBEPp+1HAH/KsoOIWB0Ri9P3b5JUkx0GHAs0z6E9i2RiI9L22ZFYCAyUNDRjvGZmVgZZC/z9XNJIYHvgsYJV99GJ5yQkjQL2Ah4GtouI1emqv5JcnUCSQF4s+Fhj2rYaMzPrFllLhRMRLwEvtWp7uMTmJUnqT5JYzouINyQV7i8kFSv/0db+JpJ0RzFy5MiOhmNmZm3InCQknQQcCmxLq26qiDgm4z76kiSImyLi52nzS5KGRsTqtDvp5bR9FZsOig9P2zYRETOAGQD19fUdSjBmZta2TGMSkq4C/gcYRTJQvabVK8s+BMwElkXE1QWr7gJOS9+fBswtaD81vctpHPB6QbeUmZl1g6xXEqcCp0TE7e1uWdr+wATgCUlL0rZvkMx0d5ukM0nm0f5iuu5u4GiSubT/Dny5C8c2Kw/PSGe9TNYk0QdY0pUDRcQfSEqOF3Noke0DOKcrxzQzs67JegvsDOBfKhmImZlVn6xXEgOBf5Z0GPA48G7hyoj4WpnjMjOzKpA1SYzl/e6mXVut8x1FZmY1KuvDdAdXOhAza1/hJESegMi6Q9YxCTMz64Xam+P6h1l24jEJM7Pa1F5308cy7MNjEmZmNaq9Oa49FmFm1ot5TMLMzEpykjAzs5KcJMzMrCQnCTMzK6lkkpB0g6QB6fsDJGWee8LMzGpDW1/8/0JSyvtNYAFQOCGQWe/RjeXBx62c0fJ+4ciJ3XZcs1LaShIvAP8m6V6SEt/7SfpbsQ0j4sEKxGZmZjlrK0n8O3A9cAnJA3N3ltgugM3KHJeZmVWBkkkiIuYCcyUNBF4DdsfdTWZmvUq7g9ERsVbSwcCzEdHUDTGZVYecxiLMqknWUuEPSNpS0qkkc0sEsBS4OSLWVzJAMzPLT6YkIWkscA+wNfBE2nw2MEXSkRGxrELxmVWdh5avyTsEs26T9WG6H5DMTDcyIj4TEZ8BRgKPAd+vTGhmZpa3rA/I7Q/sExFvNDdExBuSLgUWViQyMzPLXdYriXXAwCLtW6frzKzMxq2c4QFty13WJPFL4CeS9pe0Wfr6NHAdcFeWHaRlPl6W9GRB2xRJqyQtSV9HF6y7RFKDpKclHdGRkzIzs/LImiTOBZ4Ffk9y5bAOeAB4Bjgv4z5+ChxZpH16RNSlr7uhZaD8ZJJnM44EfiTJD+yZmXWzrLfArgWOlTQG2C1tXhYRDVkPFBEPShqVcfNjgTnp7bXPS2oA9gUeyno8s3LyHU3WW3WosmuaFDInhowmpc9fLAK+HhF/A4ax6YB4Y9r2AZImAhMBRo4cWebQzMx6t7znk7gW2AmoA1YD3+voDiJiRkTUR0T9kCFDyhyemVnvlmuSiIiXImJjRLwH/ISkSwlgFTCiYNPhaZuZmXWjXJOEpKEFi+OB5juf7gJOTkuBjAZ2Bh7p7vjMzHq7dsck0hnpJgK/iIi/dPZAkm4BDgIGS2oELgMOklRHUgvqBeArABHxlKTbSOpDNQHnRMTGzh7bzMw6J0sV2CZJVwG/7sqBIuKUIs0z29h+KjC1K8c0qwWerc7ylPXupoXA3sCKCsZiZh0wfd4zLe/PP2yXHCOxWpY1SfwE+J6kHYBHgbcLV0bE4nIHZmZm+cuaJG5Of15dZJ2nLzUzq1FZk8ToikZhZmZVKWtZDo9FmJn1Qpmfk5B0lKRfSVoqaUTadpakQysXnpmZ5SlTkpD0JeA2kkqwo4G+6arNgIsqE5qZmeUt65jERcDZETFH0lkF7QuBy8sflllOFlzR8taVX82ydzftTPEy3W8BHylfOGZmVk2yJom/AMWe1jkAeK584ZiZWTXJmiRmAD+UtH+6PELSacB/kpT7NjOzGpT1Ftj/lLQ1MA/oBywA1gPfjYj/rmB8ZmaWo8wz00XEpZKmAmNJrkCWRsRbFYvMzMxy16HpS0lKcKxL37t0t5lZjcuUJCRtCVxJMt/DFoCA9ZJmABdHxLq2Pm9W9QpufTWz92W9krgWOBw4i/dvhd0PuAIYAJxR/tDMzCxvWZPEicDxETGvoG25pJeBO3CSMDOrSVlvgX0bWFWkfRXwTvnCMTOzapI1SfwXcJmkDzU3pO+/ma4zM7MaVLK7SdJdrZoOAlZJejxd/lj6+a0qE5qZmeWtrTGJ1tXN7mi1/HyZYzEzsypTMklExJe7MxAza9+4lTMAWDhy4ibt0+c90/L+/MOKlVkz65zMkw6ZmVnvk3XSoW0k/UDS45L+KunlwlfGfdyQbv9kQdtHJc2T9Gz6c5u0XZJ+KKkhPebenTs9MzPriqzPScwGdgdmAS+RlOfoqJ8C16T7ajYZmB8R0yRNTpcvBo4imcNiZ+CTJA/zfbITxzQzsy7ImiQOAg6MiMWdPVBEPChpVKvmY9N9Q5KA7idJEscCsyMigIWSBkoaGhGrO3t8MzPruKxJ4jkqM36xXcEX/1+B7dL3w4AXC7ZrTNs+kCQkTQQmAowcObICIVpv4ilLzTaV9Yv/XOAKSXtK2qwSgaRXDR3uxoqIGRFRHxH1Q4YMqUBkZma9V9Yk0QB8CFgMbJC0sfDVheO/JGkoQPqzeRB8FTCiYLvhFC8LYtZxC65w1VezjLJ2N90CbA18jc4PXBdzF3AaMC39ObegfZKkOSQD1q97PMLMrPtlTRL1wL4R8WS7W5Yg6RaSQerBkhqBy0iSw22SzgRWAF9MN78bOJrkCubvgB/ss4pofght3EqPRZgVkzVJLAU+0pUDRcQpJVYdWmTbAM7pyvHMzKzrso5J/AdwtaTPStoufQiu5VXJAM3MLD9ZryTuTn/ey6bjEUqXK3LHk5m1r1Q9J7NyyJokDq5oFGZmVpUyJYmIeKDSgZh1uwVXeMDarB2ZkkR7Bfa6Uq7DzMrLZcOtnLJ2Ny0iGXtQQVvh2ITHJMzMalDWJDG61XJfYC/gUuCSskZkZmZVI+uYxIoizQ2SXid5KO6eskZlZmZVIeuVRCnPA3VliMPMOqD5tlezSss6cN36gTkBQ4EpwNNljsmsonpTOXAPYltXZb2SeJUPFvUTyZwPJ5U1IjPrlMKrCz9YZ+XS2Yfp3gNeARoioqm8IZmZWbXww3RmZlZSm0kia/G+iHitPOGYmVk1ae9KothYRGuRYT9mZtYDtffl3lZhvyNJ5r72mISZWY1qM0kUG4uQtBdwFfAZ4Drg25UJzczM8pZ10iEkjZZ0M/AIsAYYGxFfi4hXKhadmZnlqt0kIWmQpB8Afwb+AfhURJwUEc9VPDoz65RxK2f4qWwrizaThKRLgeeAA4FjI+KQiPhjt0RmZma5a2/g+tvAO0Aj8FVJXy22UUQcU+7AzMwsf+0lidm0fwusWdUrrGE0Lsc4zHqa9u5uOr07gpD0AvAmsBFoioj69EG+W4FRwAvAFyPib90Rj9Ue98+bdU41PQR3cES8WrA8GZgfEdMkTU6XL84nNOuJfPVg1nWZb4HNwbHArPT9LOC4/EIxM+udquVKIoB7JQVwXUTMALaLiNXp+r8C2xX7oKSJwESAkSNHdkesZj2S55awzqiWJPHpiFglaVtgnqQ/F66MiEgTyAekCWUGQH19vQfZzczKqCq6myJiVfrzZeBOYF/gJUlDAdKfL+cXoZlZ75T7lYSkrYA+EfFm+v5w4HLgLuA0YFr6c25+UZrVFnc9WVa5JwmSsYY7JUESz80R8RtJfwRuk3QmsAL4Yo4xmpn1SrkniYhYDuxZpH0NcGj3R2S1xM9HmHVNVYxJmJlZdcr9SsKsnAr72m3TK6mFIyfmGIn1VE4SZr2ME4d1hLubzMysJCcJs15s3MoZsOCKvMOwKuYkYWZmJXlMwmqOb3s1Kx8nCeuRfBdTx5VKng8tX8PCpuTPs/Dpaz+VbeDuJjMza4OvJKxmuJup85r/7B6a6dtibVO+kjAzs5J8JWE9hschqoPHKnoXX0mYmVlJvpKwHs3jEN2k+YG7gy/JNw7rdk4SVtXcxWSWL3c3mZlZSb6SMLN2PbR8DUDLQ3fWezhJmFlRHu8xcJKwblZqjMG3UlaPjiQH3w5b+5wkrCza+rLo6OCzB6vNqoeThFWFjiYGd4Xkw7Pa9T5OElb1mr+Y/KVU3QoT/biVM9hvx0HJwsGXuFuqB3OS6OUqMUZQqe4iXz1UFyfv3qHqk4SkI4EfAJsB10fEtJxDqqju+I2rK1/ilR4v8BdPz1OqC6r1bbPFKs2ev/kdLdtPb/pCy3b77TjIT3dXiapOEpI2A/4bOAxoBP4o6a6IWJpvZD1DVxJOuZNBR/uyfdXQMxX7eyvn36W7rbpfVScJYF+gISKWA0iaAxwLVDRJtPUF2ZUv2079o05r5jT/Vgaw35nf7fh+isj6W3te21ntakkczeMWbJpMHlq+BpZf+MHPFS4sGLTp9gVarlQO26Xl/1DzlUrzsT5wtVLu+lRt7a95XTmPVyGKiLxjKEnSCcCREXFWujwB+GRETCrYZiLQ/G3zj8DTnTzcYODVLoRbTXwu1alWzqVWzgN8Ls12iIghxVZU+5VEuyJiBtDl61lJiyKivgwh5c7nUp1q5Vxq5TzA55JFtRf4WwWMKFgenraZmVk3qPYk8UdgZ0mjJW0BnAzclXNMZma9RlV3N0VEk6RJwG9JboG9ISKeqtDhaul2Gp9LdaqVc6mV8wCfS7uqeuDazMzyVe3dTWZmliMnCTMzK8lJooCkb0t6XNISSfdK2j7vmDpL0lWS/pyez52SBuYdU2dJOlHSU5Lek9TjbleUdKSkpyU1SJqcdzydJekGSS9LejLvWLpK0ghJCyQtTf9tnZt3TJ0hqZ+kRyQ9lp7Ht8p+DI9JvE/SRyLijfT914CxEfGvOYfVKZIOB36XDv5fCRARF+ccVqdI2g14D7gOuDAiFuUcUmZpaZlnKCgtA5zSE0vLSDoAeAuYHRF75B1PV0gaCgyNiMWSBgCPAsf1tL8XSQK2ioi3JPUF/gCcGxELy3UMX0kUaE4Qqa2AHptBI+LeiGhKFxeSPGPSI0XEsojo7JP0eWspLRMRG4Dm0jI9TkQ8CLyWdxzlEBGrI2Jx+v5NYBkwLN+oOi4Sb6WLfdNXWb+3nCRakTRV0ovAl4D/m3c8ZXIGcE/eQfRSw4AXC5Yb6YFfRrVM0ihgL+DhnEPpFEmbSVoCvAzMi4iynkevSxKS7pP0ZJHXsQARcWlEjABuAia1vbd8tXcu6TaXAk0k51O1spyLWblJ6g/cAZzXqiehx4iIjRFRR9JbsK+ksnYFVvXDdJUQEZ/NuOlNwN3AZRUMp0vaOxdJpwP/BBwaVT741IG/l57GpWWqVNqHfwdwU0T8PO94uioi1kpaABwJlO3mgl53JdEWSTsXLB4L/DmvWLoqnazpIuCYiPh73vH0Yi4tU4XSAd+ZwLKIuDrveDpL0pDmOxclfYjkBomyfm/57qYCku4gKTf+HrAC+NeI6JG/9UlqALYEmgvtL+zBd2qNB/4LGAKsBZZExBG5BtUBko4Gvs/7pWWm5htR50i6BTiIpCT1S8BlETEz16A6SdKngd8DT5D8fwf4RkTcnV9UHSfp48Askn9bfYDbIuLysh7DScLMzEpxd5OZmZXkJGFmZiU5SZiZWUlOEmZmVpKThJmZleQkYdaDSHpB0oV5x2G9h5OE1SRJP5UURV5lq46Zk32AH+UdhPUeva4sh/Uq9wETWrVtqNTBJG2RVnqtmIh4pZL7N2vNVxJWy9ZHxF9bvV6TdKCkdyUd1LyhpK9IekPSjuny/ZJ+LOkHkv6Wvq6S1KfgMy9ImpJOxrOWtIiipE9JekDS3yWtknStpI8UfO4ASQslvSXp9XTSmD3SdVtL+lk6uc86ScslndfqmBcWLI9UMqnUm+nr55KGF6yfkhZKPFnSc+k2v5A0uAJ/3laDnCSs14mIB4CrgJ9J2kbSrsDVwL9FxPKCTb9E8n9kP+ArwETgvFa7u4CkVk498A1JHwPuJanPtCdwPFAH3AAgaXNgLsnkMHsCnyQp2bEx3d93gI+RFGb8R5Iy70VLw6QJay6wHXBw+toe+EVam6jZKOAkYDxwOElZ7B5ZGsS6n7ubrJYdKemtVm3/nc7QdxlJMbSZJF+iv4qIWa22XQ18La2g+2dJu5AkhcKCcA9ExH82L0iaDdwaEd8raPs/wJ8kbUtStn0g8MuIeC7dpLAg2w7A4oh4JF1e0cb5HQp8HNgpIl5Ij/XPQEO67r50u82B0yPi9XSbGcCX29ivWQsnCatlD5L89l9oLUBEvJt+oT5FMlnLIUU+v7BVifWHgG+rYJpboPVUqp8Axkg6qaCt+bf6nSLiIUk/BX4raT4wH7g9Ilam21wL3C7pE8A8kmTyQInz2w34S3OCSM9ruaS/AGN5P0msaE4Qqb8A25bYp9km3N1ktezvEdHQ6vVqwfpxJP8HBpJUmO2Mt1st9wGuJ+lian7tCewMLAGIiC+TdDM9CBwDPC3piHTdPSRXE98lqbb6a0k3diKuwuT2bpF1/r9vmfgfivVKkkYD1wDnkPzG/j/peEGhT7bq2x9H8pt7WzOYLQZ2L5KcGiLineaNIuKxiLgyIg4C7gdOK1j3akT8LCJOB84ETpO0ZZFjLQO2VzL9ZvN57UgyLrG0nT8Cs0ycJKyWbSnpH1q9hkjaDPgZyXjCdcBZJLPHtZ6FcHvg+5L+UdIJwL8D09s55pUkU0j+WNJeksZI+idJ10GSnCRNS++A2kHSwSTjCkvT9ZdLOk7SzpJ2Ixn4Xh4R64sc6z7gceAmSfWS6knusFoM/K7Df1pmRXhMwmrZZ0kGnwutAq4DxpDcRURErJF0GnC3pN9GxB/SbW8imczlYZIumpm0kyQi4nFJB5DcpfRA+vnlwJ3pJn8HdgH+l/cn77mJJLkArCe582g0sA5YCHy+xLFCyRzgPwQWpM33kdyl5YlirCw86ZBZEZLuB56MiEl5x2KWJ3c3mZlZSU4SZmZWkrubzMysJF9JmJlZSU4SZmZWkpOEmZmV5CRhZmYlOUmYmVlJ/x/DUQ3pJgVtBQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"bins = np.linspace(-3,3,100)\n",
"plt.hist(values[:,0],bins=bins, alpha=0.5,label=\"ts-40\")\n",
"plt.hist(values[:,-1],bins=100,alpha=0.5,label=\"ts-260\")\n",
"plt.legend(loc=\"best\");\n",
"plt.xlabel(\"Expression\", size=14)\n",
"plt.ylabel(\"Number of Instances\", size=14)"
]
},
{
"cell_type": "code",
"execution_count": 67,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXsAAAD4CAYAAAANbUbJAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAAAOzElEQVR4nO3dbYxc1X3H8e+v5KFSkxaoXdc1Jk5Tt5KRWhNtKVKqhoq0EJBqIkUUpIAbUTkvQEpU3jjJi0SVkNyHQBupRXUKiqlCCCFBWA1NCy5SGqk8rCki2JTgJKbYNfYmoQSVitbw74u9Tib22jO7M7Oz6/P9SKO5c+bcmb+PZ3979sydO6kqJEmnt5+YdAGSpPEz7CWpAYa9JDXAsJekBhj2ktSAN0y6AIAVK1bUunXrJl2GJC0ru3fv/m5VrRyk75II+3Xr1jE9PT3pMiRpWUny3KB9XcaRpAYY9pLUAMNekhpg2EtSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGLIlP0EotWLf1Kz/c3r/t8glWohY5s5ekBhj2ktQAw16SGmDYS1IDDHtJaoBH40gT5lE6WgzO7CWpAYa9JDXAsJekBrhmLy0hvev3vVzL17Cc2UtSAwx7SWqAYS9JDTDsJakBfcM+ydokDyXZm2RPkg937Z9McjDJE93lsp59PppkX5Jnklwyzn+AJKm/QY7GOQrcWFWPJ3krsDvJA919t1TVn/d2TrIBuAo4D/gF4MEkv1xVr42ycEnS4PrO7KvqUFU93m2/DDwNrDnFLpuAu6rq1ar6DrAPuGAUxUqSFmZea/ZJ1gHnA490TTckeTLJ7UnO6trWAM/37HaAU/9ykCSN2cBhn+QtwJeAj1TVD4BbgXcAG4FDwKfm88RJtiSZTjI9MzMzn10lSfM0UNgneSOzQf+5qvoyQFUdrqrXqup14DP8aKnmILC2Z/dzurYfU1Xbq2qqqqZWrlw5zL9BktRH3zdokwS4DXi6qm7uaV9dVYe6m+8Dnuq2dwJ3JrmZ2Tdo1wOPjrRqaZk72WkRpHEZ5GicdwHXAN9I8kTX9jHg6iQbgQL2Ax8CqKo9Se4G9jJ7JM/1HokjSZPVN+yr6utA5rjr/lPscxNw0xB1SZJGyE/QSlIDDHtJaoDns5eWAb+nVsNyZi9JDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWpAYa9JDXAsJekBhj2ktQAw16SGuApjqVlxtMdayGc2UtSA5zZSyPmzFtLkTN7SWqAYS9JDTDsJakBhr0kNcA3aKUx6n2zVpokw15axjzyR4NyGUeSGmDYS1IDDHtJakDfsE+yNslDSfYm2ZPkw1372UkeSPJsd31W154kn06yL8mTSd457n+EJOnUBpnZHwVurKoNwIXA9Uk2AFuBXVW1HtjV3QZ4L7C+u2wBbh151ZKkeekb9lV1qKoe77ZfBp4G1gCbgB1dtx3AFd32JuCOmvUwcGaS1aMuXJI0uHmt2SdZB5wPPAKsqqpD3V0vAKu67TXA8z27Hejajn+sLUmmk0zPzMzMt25J0jwMHPZJ3gJ8CfhIVf2g976qKqDm88RVtb2qpqpqauXKlfPZVZI0TwOFfZI3Mhv0n6uqL3fNh48tz3TXR7r2g8Dant3P6dokSRMyyNE4AW4Dnq6qm3vu2gls7rY3A/f1tF/bHZVzIfBSz3KPJGkCBjldwruAa4BvJHmia/sYsA24O8l1wHPAld199wOXAfuAV4APjrJgSdL89Q37qvo6kJPcffEc/Qu4fsi6JEkj5CdoJakBnvVSGgFPZaylzpm9JDXAsJekBhj2ktQAw16SGmDYS1IDDHtJaoBhL0kNMOwlqQGGvSQ1wLCXpAYY9pLUAMNekhpg2EtSAzzrpXSa6D3z5v5tl0+wEi1FzuwlqQGGvSQ1wLCXpAYY9pLUAMNekhpg2EtSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIa0Dfsk9ye5EiSp3raPpnkYJInustlPfd9NMm+JM8kuWRchUuSBjfIzP6zwKVztN9SVRu7y/0ASTYAVwHndfv8dZIzRlWsJGlh+oZ9VX0N+P6Aj7cJuKuqXq2q7wD7gAuGqE+SNALDfHnJDUmuBaaBG6vqRWAN8HBPnwNd2wmSbAG2AJx77rlDlCFNRu+XhUhL3ULfoL0VeAewETgEfGq+D1BV26tqqqqmVq5cucAyJEmDWFDYV9Xhqnqtql4HPsOPlmoOAmt7up7TtUmSJmhBYZ9kdc/N9wHHjtTZCVyV5M1J3g6sBx4drkRJ0rD6rtkn+TxwEbAiyQHgE8BFSTYCBewHPgRQVXuS3A3sBY4C11fVa2OpXJoA1+m1XPUN+6q6eo7m207R/ybgpmGKkiSNlp+glaQGGPaS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWpAYa9JDXAsJekBgxzimNJS1TvaR32b7t8gpVoqXBmL0kNMOwlqQGGvSQ1wLCXpAYY9pLUAMNekhpg2EtSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGeCI06TTnSdEEzuwlqQmGvSQ1wGUcqSEu6bTLmb0kNcCwl6QG9A37JLcnOZLkqZ62s5M8kOTZ7vqsrj1JPp1kX5Ink7xznMVLkgYzyMz+s8Clx7VtBXZV1XpgV3cb4L3A+u6yBbh1NGVKkobRN+yr6mvA949r3gTs6LZ3AFf0tN9Rsx4GzkyyekS1SpIWaKFr9quq6lC3/QKwqtteAzzf0+9A13aCJFuSTCeZnpmZWWAZkqRBDH3oZVVVklrAftuB7QBTU1Pz3l9aLL2HK0rL1UJn9oePLc9010e69oPA2p5+53RtkqQJWmjY7wQ2d9ubgft62q/tjsq5EHipZ7lHkjQhfZdxknweuAhYkeQA8AlgG3B3kuuA54Aru+73A5cB+4BXgA+OoWZp7Fy60emmb9hX1dUnueviOfoWcP2wRUmSRstP0EpSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIaYNhLUgP8wnGpUX75eFuc2UtSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIaYNhLUgP8BK0kP03bAGf2ktQAw16SGmDYS1IDXLOXOr3r1tLpxrCX9GOO/6XnG7anB5dxJKkBhr0kNcCwl6QGGPaS1ICh3qBNsh94GXgNOFpVU0nOBr4ArAP2A1dW1YvDlSmNnkffqCWjmNn/dlVtrKqp7vZWYFdVrQd2dbclSRM0jmWcTcCObnsHcMUYnkOSNA/Dhn0B/5Rkd5ItXduqqjrUbb8ArJprxyRbkkwnmZ6ZmRmyDEnSqQz7oarfrKqDSX4OeCDJv/feWVWVpObasaq2A9sBpqam5uwjSRqNoWb2VXWwuz4C3AtcABxOshqguz4ybJGSpOEsOOyT/FSStx7bBn4XeArYCWzuum0G7hu2SEnScIZZxlkF3Jvk2OPcWVVfTfIYcHeS64DngCuHL1MaDQ+3VKsWHPZV9W3g1+Zo/x5w8TBFSaNkwEt+glaSmmDYS1IDDHtJaoBfXiLplHrf8/CLTJYvZ/aS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWpAYa9JDXA4+wlLYjH3y8vzuwlqQGGvSQ1wGUcnZY8rfF4OK7Ll2Gv04ZBJJ2cyziS1ABn9pKG5pE5S59hr2XBMJGG4zKOJDXAsJekBriMo2XHo26WNpfcliZn9pLUAGf2ksbGWf7SYdhrSTEcpPEw7LVkuTYvjY5hL2nRnewX+cn+mvMvvuEZ9horf0ilpcGwl7QoBlmWc3IwPmML+ySXAn8JnAH8bVVtG9dzaTJO9oPpD7XGydfOwqSqRv+gyRnAN4HfAQ4AjwFXV9XeufpPTU3V9PT0yOtY7ub7ol7ID8Ega6e+Uaqlar6v00H6n6zPUvzFkmR3VU0N0ndcM/sLgH1V9e2uoLuATcCcYT+MYf8zBpmdDhO043ixDDtznu/+0lI139fpMK/r4/cd5ud5Er9ExjWzfz9waVX9YXf7GuA3quqGnj5bgC3dzV8Bnhl5IZO3AvjupItYghyXEzkmJ3JMTnT8mLytqlYOsuPE3qCtqu3A9kk9/2JIMj3on1gtcVxO5JicyDE50TBjMq5z4xwE1vbcPqdrkyRNwLjC/jFgfZK3J3kTcBWwc0zPJUnqYyzLOFV1NMkNwD8ye+jl7VW1ZxzPtcSd1stUQ3BcTuSYnMgxOdGCx2Qsb9BKkpYWz2cvSQ0w7CWpAYb9CCU5O8kDSZ7trs+ao8/GJP+aZE+SJ5P8/iRqXUyDjEvX76tJ/ivJ3y92jYshyaVJnkmyL8nWOe5/c5IvdPc/kmTdBMpcVAOMyW8leTzJ0e7zO00YYFz+KMneLkN2JXlbv8c07EdrK7CrqtYDu7rbx3sFuLaqzgMuBf4iyZmLV+JEDDIuAH8GXLNoVS2i7hQifwW8F9gAXJ1kw3HdrgNerKpfAm4B/mRxq1xcA47JfwB/ANy5uNVNzoDj8m/AVFX9KnAP8Kf9HtewH61NwI5uewdwxfEdquqbVfVst/2fwBFgoE/ALWN9xwWgqnYBLy9STYvth6cQqar/BY6dQqRX7zjdA1ycJItY42LrOyZVtb+qngRen0SBEzLIuDxUVa90Nx9m9rNMp2TYj9aqqjrUbb8ArDpV5yQXAG8CvjXuwiZsXuNymloDPN9z+0DXNmefqjoKvAT87KJUNxmDjEmL5jsu1wH/0O9BPZ/9PCV5EPj5Oe76eO+NqqokJz2uNclq4O+AzVW17GctoxoXSYNL8gFgCnh3v76G/TxV1XtOdl+Sw0lWV9WhLsyPnKTfTwNfAT5eVQ+PqdRFNYpxOc0NcgqRY30OJHkD8DPA9xanvInwtCpzG2hckryH2cnUu6vq1X4P6jLOaO0ENnfbm4H7ju/QnT7iXuCOqrpnEWubpL7j0oBBTiHSO07vB/65Tu9PPXpalbn1HZck5wN/A/xeVQ02eaoqLyO6MLu+ugt4FngQOLtrn2L227oAPgD8H/BEz2XjpGuf9Lh0t/8FmAH+h9l1yksmXfuIx+EyZr/U51vM/lUH8MfdDyzATwJfBPYBjwK/OOmal8CY/Hr3WvhvZv/K2TPpmpfIuDwIHO7JkJ39HtPTJUhSA1zGkaQGGPaS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWpAf8PJxHm/X3mia4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plt.hist(values.mean(axis=1),bins=100);"
]
},
{
"cell_type": "code",
"execution_count": 68,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZQAAAEKCAYAAAA1qaOTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAABJB0lEQVR4nO29d5hkdZX//zpVXdU5p8l0z3QLDCJpmCEMihJNIEowY0BEZZVVf65+XVdXV3d118Wsq4iiqICggIowgChhYJghM0OYyOTOubtS1+f3x61bXdNT3V3h3qrq7vN6nvtM1a1bXZ++U33PPel9xBiDoiiKomSLJ98LUBRFUeYGalAURVEUR1CDoiiKojiCGhRFURTFEdSgKIqiKI5QlO8F5JOGhgbT0tKS72UoiqLMKp544oluY0zj5P3z2qC0tLSwadOmfC9DURRlViEiryTbryEvRVEUxRHUoCiKoiiOoAZFURRFcQQ1KIqiKIojqEFRFEVRHEENiqIoiuIIalAURVEUR1CDoigFxtaOIR7b0ZPvZSg55IlX+oiMR/O9jKxRg6IoBcZ37tvKv9z2bL6XoeSIPb2jvOPH67nzmf35XkrWqEFRlAKjdyRE70go38tQcsTevjEAXu4YzvNKskcNiqIUGP1jYYYCkTkRAlFmpms4CMDObjUoiqI4zMCo5Z0MjIXzvBIlF3QOBgDY1T2a55VkjxoURSkw+mOGpF8Nyrwg7qH0jBCNmjyvJjvUoChKARGMjDMaGgegf1QNynyga8gyKKFIlP0DY3leTXaoQVGUAiIxzNU/qon5+UDXUBCvR4DZH/ZSg6IoBcTgIQZFPZT5QNdQkGMWVQGzPzGvBkVRCohEI6I5lPlB51CQVy+uptTnZad6KIqiOEWiQRnQkNecJzwepXckRFNlMS0N5eqhKIriHIleiXooc5/uWIVXU2UJyxvK2dWjHoqiKA5hJ+Lryv30aQ5lzmNXeDVWFtPSUMbu3lHCs7ihVQ2KohQQA2NhPAJLa0u1ymse0DloeyjFtDZUMB417OmdvV6KGhRFKSD6R8NUl/qoLfdrp/w8wG5qbKwsprWhDIBdPSP5XFJWFJRBEZHzReQlEdkmIp9P8vprReRJEYmIyMWTXrtcRLbGtstzt2pFcY7+sTA1ZX5qSn1aNjwPsD2UhgrLQwHY0TV7DUpRvhdgIyJe4IfAOcBeYKOI3GmM2ZJw2G7gA8BnJ723DvgysAowwBOx9/blYu2K4hT9oyGqS33UlPnp05DXnKdrOEBtmQ9/kYdar4+qkiL1UBxiNbDNGLPDGBMCbgIuTDzAGLPLGPMsMDlrdR5wrzGmN2ZE7gXOz8WiFcVJBsbC1JT5qC71qeLwPKBzMEhTZQkAIkJrYwU7u9WgOMFiYE/C872xfW6/V1EKhv7RMDWlPmrLfAAMBiJ5XpHiJl3DQRori+PPW+vLZrX8SiEZlJwgIleKyCYR2dTV1ZXv5SjKIfSPhqwcSpk//lyZu1geSoJBaahgX/8YgfB4HleVOYVkUPYBSxOeL4ntc/S9xpifGmNWGWNWNTY2ZrRQRXGD8ahhKBihutRHdcxD0ebGuYsx5nAPpbEcgFdmaYNjIRmUjUC7iLSKiB94J3Bniu+9BzhXRGpFpBY4N7ZPUWYNQ4EwxkBNmY+a0phBUQ9lzjI4FiEUiU4KeVkGZbZKsBSMQTHGRICrsQzBC8AtxpjNIvJVEbkAQEROFpG9wCXA/4nI5th7e4GvYRmljcBXY/sUZdZglwlXl/qojYe81EOZq3QNW5MaEw1KS6wXZccsTcwXTNkwgDHmLuCuSfv+LeHxRqxwVrL3Xg9c7+oCFcVF7PBWTZmPGjvkpQZlzjLRJV8S31dZ4qOhophds9SgFIyHoijzHTu8VV3qp7LEh4jmUOYyiV3yiSxvKJ+1pcNqUBSlQBhI8FC8HqGqxKc5lDlM3EOpOtSgtDSUzdq5KGpQFKVAsMNbdkK+pkzlV+YyXcNBios8VBYfmnlobaigezjIUGD2/d+rQVGUAiExKQ9QU+bXkNccpnMwQFNVMSJyyP64SOQs9FLUoChKgdA/FqKyuIgir/VnWVPq06mNc5iu4SCNFcWH7Y+LRM7C0mE1KIpSIAyMhuMNjRALeamHMmdJ1PFK5Ij6MkSYlYl5NSiKUiD0x4QhbWpKffSNqIcyV5ncJW9T4vOyqLp0VpYOq0FRlAKhfzRETak//rymzM9gIMJ41ORxVYobBCPj9I+GD9HxSqR1lpYOq0FRlAJhYOzwkBfAoIa95hzdw5bnmcxDAbt0eARjZtfNhBoURSkQBsbC8ZJhmDAomkeZe3QOWrIrk3tQbFobKhgMROidZSFPNSiKUgAYY+Lz5G3s8Jc2N849uoZiXfIVhyflgVk7X14NiqIUACOhcSJRc0hSvlr1vOYsnUPJu+RtZut8eTUoilIA2F5IYlI+rjg8ph7KXKNrKIgI1Jf7k76+pLYUr0fUQ1EUJX3iXfKTyoYTX1PmDp1DQerL/fEm1sn4vB6W1ZXNukovNSiKUgDEhSETcihValDmLF1DQRqSdMkn0tpQriEvRVHSJy4MWTYRArEUh4s0KT8H6RoO0lSVPCFv01Jfzis9o0RnUR+SGhRFKQDsPEliUt56rgKRc5GuwUBSHa9EWhvLGQuP0zEUyNGqskcNiqIUAJOVhm1qVcJ+zmGMiXkoMxiU+Hz52RP2UoOiKAXAwFiYEp+HEp/3kP3V6qHMOfpHw4THTUoeCqhBURQlTSbreNmohP3cY6rRv5NZWFVCcZFnVolEqkFRlAJgYJLSsE1NmY8+DXnNKeKjf2cwKB6P0FI/u0Qi1aAoSgEwWXbFxlIcDqvi8Byia9hKss/koYAlErlDDYqiKOkwMDaFQSn1YQyzcr64kpy4hzJD2TBYEix7ekeJjEfdXpYjFKVykIiUAJ8CzgKamGSIjDGvcX5pijJ/6B8N85olyUNe9uuJPSrK7KVrKEipz0u53zvjscsbygmPG/b1j3FErOqrkEnJoAA/Ai4Cfg+sB9T/VhQH6R8LJTUYtkHpGw3RQuFfUJSZ6RyySoZFZMZjWxomKr3mkkF5G3CJMeY+F9eiKPOSQHicQDiaNORVbUvYa+nwnKFrKDhjybBNa4JBOfNIN1flDKnmUEaBPW4uRFHmK3EdryRVXrWxfQNa6TVn6BwKzNjUaNNQ4aeiuGjWlA6nalC+BXxaUvHRFEVJi7iOV7I+lDIdsjXXSMdDERFLJHKWGJRUQ17nAGcA54vIFuCQ2yVjzAVOL0xR5gvxWShJPJSqEutPVENec4NAeJzBQCSlCi+bloZynt7T5+KqnCNVg9IN/NHNhSjKfMU2FslyKEVeD5UlRa7qeXUOBagt8+ObYjaH4hwTo39T81DAyqP8+dn9BCPjFBfNXBmWT1IyKMaYD7q9EEWZrwyMTp1DAWtyo1shr2jUcO61D3LZqqV84U1Hu/IZygT26N/GFHMoYM2XNwZ294zS3lzp1tIcIa1bEhFZLiJvEZE3i8hytxalKPOJCen65H0mNWU+10JefaMh+kfD3LJpD8HIuCufoUyQmYdizZefDRIsKRkUEakSkd8D24DbgTuArSJyi4gUtslUlAJnYCxMkUembHSrLnVPwt6+Y+4bDXPflk5XPkOZoCs22yTVKi+YXTL2qXoo3wVeA7weKI1tZ8X2fceVlSnKPMHqgvdN2ehW42LIyzYoHoGbN2lngNt0DQXxCNSXp25Qqst81JX72dUzdwzKBcAVxph/GGPCse3vwJVYTY+KMmcZDkb42YM7XBNo7B8Lx+fHJ6Om1L2QV+egdcd84fGLeWhrF/v6x1z5HMWicyhIfUUxXk96HRizZb58qgalFOhJsr8XSL3+TVFmIes2H+Trd73Ac/sGXPn5A6NhaqYxKLVlPgbGwq7MFrc9lI+fuQJj4LYn9jr+GcoE6fSgJNJSXz6nPJRHgK+JSJm9Q0TKgX/H0vZSlDnLgQHrLr5j0J3Z3lPpeNlUl/ljisMRxz+7czBAZUkR7c2VnN5Wzy2b9rhiuBQLW8crXZY3ltMxGGQk6Px3wElSNSj/DJwC7BORf4jIP7CkWNYA17i0NkUpCA4MWGGgTrcMygweiv2aXQ3mJJ1Dwfigp0tXLWVv3xiP7kgWjFCcIBsPBQo/MZ+SQTHGPA+0A58DNsW2zwHtxpjNTi1GRM4XkZdEZJuIfD7J68UicnPs9Q0i0hLb3yIiYyLydGz7iVNrUpQD/ZYhscNDTjMwGqZ6ih4USFQcdj6PYhkUK2p93jELqCop4uaNmpx3g2jU0D2cmYdii0QWetgr1U55jDGjwM/cWoiIeIEfYsm87AU2isidxpgtCYd9GOgzxrSJyDuBbwKXxV7bbow53q31KfMXO+RlD0ZykvB4lKFgJKmOl42bel6dQwFOXFYLQInPy9tOWMxNG/fMaOSU9OkbDRGJmsw8lAYr27CzwBPzU3ooIvJ2EfElPJ5yc2gtq4FtxpgdxpgQcBNw4aRjLgRuiD2+FThLBSsVt7FDXh1Dzoe8BqdRGraxXxtwuNLLGEPnYPCQ2eaXrlpKKBLljmf2OfpZyoSHm46Ol02Zv4gFVSXsnMUeyq3AAqAz9ngqDOCEwMxiDpXI34uVo0l6jDEmIiIDQH3stVYReQoYBP7VGPNQsg8RkSuxyp1ZtmyZA8tW5jKB8Hg81OSGh9KfikGxcygOh7wGAxGCkSjNCRe4Vy+u5phFVdy8cQ/vP7XF0c+b78S75FOYJZ+M1oby2ZtDMcZ4jDGdCY+n2gpBrewAsMwYcwLwaeC3IlKV7EBjzE+NMauMMasaGxtzukhl9mGHu0p9XldyKLaRSCYMaWO/1udwyMvu2p58gbt01VI27x/keZfKpOcrcQ8lQ4PS0lBe8HNRCkledB+wNOH5kti+pMeISBFQDfQYY4LGmB4AY8wTwHbgVa6vWJnz2OGuYxdX0zMSJDIedfTnD8yg4wUxxeFi5xWHbY/LTsrbvO34xfiLPNyinfOOkq2HsryhnL7RcEHPxklVy+tSETk34fm/icheEblHRBY6tJaNQLuItIqIH3gncOekY+4ELo89vhj4mzHGiEhjLKlPTLSyHdjh0LqUeYxd4XXc0mqMge5hZ/+YJ4ZrTZ8Aryn3OZ5DmYjpH3qBqy7zcf4xC7j9qX0EwioY6RSdQwEqioso86dcC3UIifPlC5VUPZSv2A9E5ETg/wHfA3zAt51YiDEmAlwN3AO8ANxijNksIl8VEXuA18+BehHZhhXaskuLXws8KyJPY+V7rjLG9DqxLmV+czDWe/KaJTWAdVFwkunG/yZSU+q8npf9uyQLwVx28lIGAxHu2XzQ0c+cz3QNBTP2TuDQ+fKFSqqm8gjgpdjji4DbjTHfEpF1WAbAEYwxdwF3Tdr3bwmPA8AlSd53G3CbU+tQFJv9/WPUlvlYVmeVbXY4nJjvHw0jApUlMxgUFyTsOwaDlPq8VBQffhk4dXk9S2pLuWXTHi48frGjnztf6czSoCyrK8MjhW1QUvVQAoAtU38WcF/s8UDCfkWZcxwcCLCgujReCeWGh1JZXDSjWKAbEva2DEiyynuPR7jkpKU8sq2HPb2jjn7ufKU7S4PiL/KwpLZsThiUh4Bvi8iXgFVMeBGv4tBSX0WZU+wfCLCouoSGCj8izpcO949Or+Nl48bUxs7BwLQVRxevWoII/F6T846QKHOTKS0FXjqcqkG5GghhJcKvMsbsj+1/Iw6GvBSl0Dg4MMaC6hKKvB7qy/2Oeyj9Y+EZ8ydghbycVhzuSpBdScbimlLOaG/k1if2uibdP18YDUUYDkay8lDAqvTa1T2CMYX5/5GqltdeY8xbjTHHGWOuT9h/jTHmk+4tT1Hyx1jIampcWG1ddJsqS1zwUMLT9qDYVJf6iBoYclBtNpWY/mWrlrJ/IMDD27od+9z5SPeQ5V1OZ8BTobWhnJHQeLwEudBItWy4UUQaE54fKyL/ISLvcm9pipJf7AqvhdWlgFVe63Rz48BYOKWQl33MgEN5FPuOuXkGGZCzVzZRW+bjFhWMzIrOKZpI06XQS4dTDXndArwVQEQagAexqr1+IiKfcWltipJX7KbGCQ+l2PGZKP2joRl7UGCiT8WpbvmJpsbpL3DFRZZg5LotB+kdKdyGukIn3tSYgTBkIsvniEF5DfBY7PHFWCKOxwDvBz7qxsIUJd/YTY0LaywPpbmqhO7hoGP5hGjUxDyUmQ1Kbbk9E8UZD2WqpsZkXHbyUsLjhtufUsHITEnnfE/HoppS/F7PrDcopcBw7PHZTHSwP8mhcimKMmewQ14LqiY8lKiBnmFnwl5DwQhRM72Ol011qbMS9hNNjTPH9I9aUMVxS6q5ZdOegk0GFzpdQ0G8HqEuhfDmdHg9wrL6wi0dTtWgbAXeLiJLgXOBdbH9zUC/C+tSlLxjNzWW+i3906Z4L4ozBsXOh6SWQ3FWwj7VkJfNpScv5cWDQzy7VwUjM6FzKEBDhR/PDP1GqdBSX7ilw6kalH/HGma1C3jMGLMhtv884CkX1qUoecduarSxL75OlQ7bI31TyaHEFYdHnAt5+b2elMJtAG89bhElPg83a09KRmQru5LI8sZyXukdLchS7lTLhv8ALMNqajw/4aX7sDS1FGXOYTc12tgeilPyK6nqeAH4vB4qioscmyvfORigsTJ5l3wyqkp8vOnVC/nT0/sZC6lgZLp0ztDzkw4t9eWEIlH294858vOcJGX5emNMhzHmKaBRRDyxfRuMMS+6tjpFySN2U6ONXaHjVC9KXGk4RS+hpsznWNlwJrpSl568lKFghL8+f8CRNcwnuoaCWVd42RTyfPlU+1B8IvItERnCmknSEtv/TRH5uIvrU5S8YDc1LqqZCHn5izzUOdgtb1dsVaUQ8gJnBSI7h6aXXUnGmtY6WurLuFl7UtJiPGroHg5mXeFls7yxcEuHU/VQvozVh/JeIPH27HHgAw6vSVHyzuQKLxurF8WppLwVvkqlyguclbC3hSHTQUS4ZNVSNuzsLfjJgYVE70iIqMm+qdGmqbKYMr93VhuUd2FpeN0BJI6sex6djKhkwX/e9QL/8ectjk9CzJYDsfj0wppJBqWqJD46N1v6R8OU+b0UF6U2Rbu6zBnF4WBknP7RcEYx/XecuASPoNMc02C6uTOZICIFW+mVqkFZBLySZH8Rqc9UUZRDGAuNc/0jO7nu4Z1cdeMTBZXstWfJL0yo8gLrouBU2XD/WDilCi+bWodCXnbXdnMGIZgF1SWceWQTtz6xt+BuAgqVbEf/JqO1QFWHUzUom7GmIk7mUuAJ55ajzCc2vdJLeNxw4fGLuP/FTt5z3WMFMy97suyKTVNlMV1DQUdUf/tHw1Sn0ehmh7yy/ex413aGVUeXrlpK51CQB7d2ZbWO+UK25zsZrQ3l7O0bIxQpLKOeTh/K90Xki4AXuEREfoE1gvdrbi1Omdus395DkUf4xkXH8sN3n8jz+wa5+CePFkQ55IGBALVlPkp8h4ajmqtKiEQNvQ4YvoGx1HS8bGrKLMXh4VB2isN2lVqmd8xnHd1EQ4V/Tifn+0ZCDAWcKYBww0NpaShnPGrY01dYw89S7UP5E5Y3ci5WDuXLQDvwVmPMfdO9V1GmYv32Ho5fWkN5cRFvOnYhN3xoNR0DAd7+o/W83DGU17UdGAgcFu6ChOZGBxLz/aOp6XjZ2Mn7/iybG+0cUKZVRz6vh4tOWMz9L3QWrIx6trz7ug189vfPOPKzuoaCVJYUHXZzkg3x0uECC3vNaFDskmHgRWPM64wxFcaYMmPMWmPMupneryjJGAyEeW5vP6etqI/vO3VFPTd/9FSixnDxj9ezcVdv3tZnGZTDQxT2RbjDgcR8qsO1bGyJlmybGzuHgngE6sszv2O+ZNVSIlHD3ZsPZrWWQmR71zAvHBjkkW09juSJnOySt2ktUNXhGQ2KMSYMfBzIXoRGUWI8vqOXqIFTVzQcsn/loipu+9hpNFQU897rNrAuTxesAwNjh1V4wUQcvCtLD8UYw8BoOC76mAq1MeOTbaVX52CQhoriGefYT0d7UwWLa0p5eA7mUe7d0gHAcDDCCwey95Qz6fmZidoyH9WlvtlnUGLcA7zBzYUo84v123soLvJwwrKaw15bWlfG7686laMWVnHVjU/wu8d353RtYyGrrDZZyKvRIT2vsfA4ofFomh6KMxL2HUOBrJvsRIS1bQ2s395TkJpS2XDvlg4WxxpaN+zsyfrnWR6Kcwl5sM5/IVZ6pWpQ7ge+ISLfEZH3icjbEzc3F6jMTdZv72ZVS+2UceX6imJ+95E1nNHeyBf+8BzfvW9rzqTTp6rwAijxeaku9WXd3BjX8UojKW97MwNZFgR0DjqjK7W2vYGhQIRn9/Zn/bMKha6hIE/u7uOSVUtoqS9jw87sw66WjpezHgoUZulwqgblB0AT8EngBuDWhO337ixNmav0DAd58eAQp00Kd02mzF/EdZev4u0nLuba+17mS3c8n5O74YOxHpQFSQwKWP0b2Xoo6ep4QYLicLYhL4cucKe3Wf9/D2+dO/Pm//ZiB8bAOSubWd1ax8ZdvVmVaY8EI4yGxh3PoYBlUA4MBAqqfyvVKi/PNJtzpQvKvOCxHdZd36kJCfmp8Hk9fPuS4/jo65Zz42O7+cRvniQQdvcPaH/MoCxKEvICK4+SbXOjbVBS1fECS0usorgoqxxKZDxKz4gzBqWu3M8xi6p4eNvcMSjrNlvhrpULq1jTWk//aJiXsqg4nOhBccegADy3r3Bm1KSsNqwoTrF+ezcVxUW8ZnF1SseLCF9449F86S0ruXvzQS6//nHHBk0l42As5DWVh9JUWZx12fBAfBZKehP8qkt9WVV59YyEMGZCij9b1rY38OTuPkaC2fXGFAKjoQgPb+vmnJXNiAhrltcB8HgWYS83elBszjyykZoyHz98YJvjPztTUjYoIvI2EXlQRLpj20MicpGbi1MyZzgY4YGXOh3p6HaaR3f0sLq1jiJvevczH17bynffeTxP7u7jsv971DHV38nsHwhQV+6fMr9j6XkFs8rpZBLyso/PRsI+3UmNM3FGWyPhcZPVRbdQePDlboKRKOeubAZgSW0Zi2tKs0rMpzNqOV0qS3xc9boV/OPlrryW2CeSqnz9Z4CbgZeAz8W2F4Hfishn3VuekglPvNLLm777EB/8xcaCm7B3cCDAjq6RQ/pP0uHC4xdz/QdOZlvnMNc/vMvZxcU4OBA4TGU4kabKYkLj0axCT/1pDNdKpKbMR18WSfn4Bc4hD2VVSy3FRR4emgN5lHVbDlJd6uPk1rr4vjWtdTy+szfjmwc3PRSA9596BA0VxfzPPS/lrGhlOlK9RfwscLUx5iPGmOtj20ewkvSfcW95SjqEx6P877qXuOQnj2IwHLu4mv/664t0DxdON/OjO6wLTyr5k6k4o72RtqYK17rp9/ePsShJD4qNE82N/aNh/F4PpWl2T9eU+rMqG3Y6pl/i83JySx2PzPI8SmQ8yt9e7OQNRzXhS/CcV7fW0T0cYntXZtVUnUNBfF5Jq5ovHcr8RVz9+hVs2NnL+u3ZlzhnS6oGpQJ4IMn+B2KvKXlmZ/cIF//kUb73t228/cQl3PXJM7j2suMZDUX4+l9eyPfy4qzf1kNNmY+jF1Rl9XPamirY1jns0KoO5eBgYMr8CVh6XpCd/MrAWIjqMl/KI3htnAp5NTg0PRCsPMpLHUN0DroTgswFm17po380zDmxcJfNmuXWjU+mYa+uIauJ1JNFE+lMvGvNMhZVl/A/6/LvpaRqUG4HLk6y/x3AnY6tRkkbYwy/e3w3b/ruQ+zqHuFH7zmR/7nkOCpLfLQ1VXDV61bwx6f2FURppzGG9dt7OHV5fdZ/YO1NlezpG3W8ZHK6pkabuJ5XFpVe/aPpSdfb2FMbM71wdA5Z+SF/kXP1OGvt8uFZ7KWs29yBv8jDa1/VeMj+lvoymiqL2bAjsxyFWz0oiRQXefmns9p5anc/f3ux09XPmolUv1XbgM+LyD0i8pXYdjfwBeAlEfm0vbm3VGUyPcNBPvKrJ/jCH57jpCNqueea1/KmYxcecswnXt/GEfVlfOmO510vt52JPb1j7Osfyzh/kkhbUwXGWLpLTjJdU6ONnWDtyOKOPF1hSJuaUj/jUcNwhlVVHYPOX+BWLqyirtxfEDctmWCM4d4XDnL6inoqig8d7yQirM4ij+KGjlcyLj5pCUfUl/HtdS/ntRAnVYPyAaAPazrj5bHtyNi+DwL/FNuudn6JhcftT+3Le1XFAy92ct53HuLBrV186S0r+dWHVicN05T4vPzH217Nzu4RfvT37XlY6QTrt9v5k+kbGlOhvdmKtDptUA5OMVgrkVK/l8qSoqyUdvvH0tPxsqnOUs+rayjg+AXO4xFOW1HPw9u68x5yyYSXOobY0zvGOSsXJH19zfJ6Dg4G2N2bvlS8db6dr/CajM/r4Zqz29lyYDCvgp2pNja2prgtd3vB+SYUifLDB7Zx+fWP89iO3CfBxkLjfOn25/ngLzfSUOHnzqtP58NrW6cNIZ3R3sgFxy3iJ3/f7vgFOB3Wb++hqbKYFY3lWf+slvpyvB5ha4ezv8/+uEGZ/iJgzZbP3EMZGA1l5KHU2orDGRoUKwTj/AXujPYGOoeCbHUpr+Um6zZ3IAJnr2xK+vopsaqvdMNeVhNpKCceCsAFxy2mramC/7335bzpq6VaNjxlB5qIzHkjkoi/yMNvPrKGxTWlfOAXj+e0uuX5fQO85fsP8evHXuGKta3c/onTOSrF5Pa/vuVoSnwevvjH5/JyF2nnT05bUZ92IjoZ/iIPR9SXOZ6Yn6mp0aa5Krtu+YE0x//aTAhEpl86HI0auoaCWQtDJmNtu5V7mI3lw/du6eD4pTVTGtq2pgrqyv1p63rFm0hzZFC8HuHT57yKbZ3D3PH0vpx85mRSDXk9KyKHjQAWkQ8BTzu6ollAU2UJv7vyFFrqy/nQLzfy95fcTYSNRw0/+vs23vbDRxgJjvObK9bwr29ZmdbAnqbKEv7ljUfx2I5e/vBk7r9s2zqH6R4OzqjflQ7tTRVs7XS2dHimpkYba7Z8Zh5KKBJlJDSeYQ4l85BX32iISNTQ7MIFbnFNKcsbymednP2BgTGe2zdwWHVXIiLC6pa6tCu93O5BScb5xyxg5cIqvnPfVsIOzHJJl1QNym+B+0TkGyLiFZFaEbkN+A5wjVuLK2QaKor57UdOYUVjBVf+6gnuf6HDlc/Z2zfKu372GN+6+yXOO2YBd19zRlyUL13edfIyTlxWw9fveoG+kdzObrdr5LPpP5lMW1MFu3pGHZ2rPVNTo01TVQkdg5l1y9uyMdUZeCgTOZT0///iPSgONTVO5vS2Bjbs7C24OefTcV9s9sm5U+RPbNYsr2Nvn1VUkioTXfK5Mygej/DZ817F7t5Rbn1ib84+N/75qRxkjPkC1vjf9wKPA88CS4ATjTHXO7UYETlfRF4SkW0i8vkkrxeLyM2x1zeISEvCa1+I7X9JRM5zak3TUVfu57cfWcNRCyu56sYnuMfBZJgxhtuf2scbv/MQW/YP8j+XHMcP3n1CfGpfJng8wtcvOpaBsTD/9dcXHVtrKqzf3s3SulKW1pU59jPbmyoZjxpe6XFOwnumpkabpspiQpEog2PpV1vZOl7VGfxf2tpfmXgobgoVgtWPMhoa56ndfa78fDdYt6WD5Q3ltDVN3063utXW9UrdS8mHhwLw+iObOGFZDd+7f2vOKzvTKUZ/GPgrcALQDHzVGOOYKpmIeIEfAm8EVgLvEpGVkw77MNBnjGkDrgW+GXvvSuCdwDHA+cCPYj/PdWrK/Pz6w2s4ZlE1n/jNk/zl2QNZ/8yB0TCfvOlprrn5aY5cUMlfP3UGF5+0xJHcw9ELq7hibSs3b9qTM/2l8ajhsR29nLbcuXAXEL8IOJkInqmp0ca+y88k7BXX8crAQ/EXeSj3ezPqlrcbD91IyoPlfXpk9vSjDAbCPLajZ9pwl81RC6qoKilKKzFvGxQnm0hTQUT47LlHcmAgwE05Hk6XalL+VcAG4BzgTOBrwB9E5FoRyfyW+VBWA9uMMTuMMSHgJuDCScdciDWPBaxZLGeJdZW9ELjJGBM0xuzE6ptZ7dC6ZqS61MevP7ya45fW8MmbnsoqIbZ+ezfnf/dB/vrcAf6/847k5o+e6uhdPcCnzm5ncU0pX/zjczkJT7xwYJCBsTCntTkX7gJY0ViBCI4l5lNparSx7/IzGbSVqTCkTU2ZPzsPxYWkPEBViY/jltbMGoPy95e6CI8bzj1mZoPi9Uz0o6RK51CQ6lJfWrlOpzhtRT2nLK/jBw9sZzSUOyXoVD2Up4AXgOONMQ8aY74GvBZ4M7DJobUsBhKVDPfG9iU9xhgTAQaA+hTfC4CIXCkim0RkU1eXcwnEyhIfN3xoNauOqOWfb36a29KMXwYj43zjrhd4z3UbKPV5+cPHT+MTr2/Lau73VJT5i/jqhcewtXOYnz20w/GfP5l4/8lyZw1Kqd/LktpSxzyUVJoabZqz8VDi0xozuxerLvXFw2bp0DUUpLKkyNUL3BltDTyzp9/V8QJOsW7zQRoq/By/tDal41e31rGjeyRliZlcNTUmw/ZSuoeD/OrRV3L2uakalI8aY95rjBm0dxhjNgAnYuVUZg3GmJ8aY1YZY1Y1NjbO/IY0KC8u4pcfXM2pK+r57K3PcPPG1NzNlzuGeNsP1/PTB3fwnjXL+PMn1/KaJTWOrm0yZx3dzPnHLOB7929ld0/6DVvpsH57D21NFa4kg9saK9jqkEjkgRSaGm2ykV+xE+rVGXsovoymNnYOBVxPEK9tbyRq4NECECqcjlAkyj9e6uKso5pTvmlb02rreqXmpeRCdmU6VrXUceaRjfzkH9sZCuTGwKealL9xiv3DxpgrHFrLPmBpwvMlsX1JjxGRIqAa6EnxvTmh1O/l55efzBntjfzLbc9x42NT3x1Eo4ZfPLKTt3z/YToHA/z88lX8x9uOpcxfNOV7nOTLF6ykyCN86Y7nXetNCY9HeXxnryNyK8lob65kR/eII41cB1JsagTr5qHc782ouXFgLIxHoLI4s//nmjJfRlVeHQ7Nkp+OE5bVUO738vC2wi4ffmxHD0PBSErhLptjFlVR7vemHPbKp4di85lzjqR/NOzaqIfJTGtQROS3IlKZ8PyqSc9rReRBh9ayEWgXkdZYXuadHC48eSeW7AtYYpV/M9aV8E7gnbEqsFagnTx6TiU+Lz9930mcdVQT/3r78/zykZ2HHdMxGODyXzzOv/9pC2e0NXD3Na/lrKNT/3I7wcLqUj573pH84+Uu/vJc9sUEyXh2bz+joXHXDEpbYwWhSJQ9GchiTOZAf2pNjTaZNjf2j4apLvVlLJBZU+bPKKTUORRwLX9i4/N6WLO8nke2FbaHsm7LQUp93rRK8Iu8Hk5KsR/FGJMTj3Amjl1SzXnHNHPdQzsyuglJl5k8lMuARP//W0BinMgPnO7EQmI5kauBe7DyNbcYYzaLyFdF5ILYYT8H6kVkG/Bp4POx924GbgG2AHcDnzDG5FUJscTn5cfvPYlzVzbzlT9t4bqEXMXdzx/g/O88yMZdvXz9oldz3eWr8nYn8/5TWzh2cTX//qctDLrgFq/f1oPIRLjAadpiml5OJOYPDKbW1GjTWFlMVyZJ+bFwVuXfNaU++kfTUxw2xtDpgjBkMta2NbCze4S9fe6GUjPFGMN9Wzp57asa0s4nrWmt4+WOYXpn6OMaDkYIhKN591AAPn3OkQyHIvzfg+7nS2cyKJNvodwT9QeMMXcZY15ljFlhjPl6bN+/GWPujD0OGGMuMca0GWNWG2N2JLz367H3HWmM+aub60wVf5GHH77nRN587EL+4y8v8N37tvK5W5/hqhufZGldGX/55Bm8Z80RjpQDZ4rXI3zjomPpGQ7y33e/5PjPX7+9h5ULq6gtd6oY8FCcLB0+0D+WUrjLpqmqJKMhW/2joYyaGm1qynxEooaRNKT7BwMRgpGo6yEvsHS9gIJVH35u3wAHBwNTikFOxykpzpmf6Plx/3zPxJELKrnguEX88pFdWQmapoJzQxGUpPi8Hr77zuO54LhFXHvfy9z6xF7+6Q1t3Pax01jRWBizyY5dUs37T23hxg2v8PSefsd+biA8zhO7+1wLd4FVqtpcVeyIBMuBgUBaBqW5spjODLrlB8cyk663savD0lE76IqP/nX/jrmtqYLmqmIeKtDy4XWbO/AInHVUcjHI6Th2cQ0lPs+MYa98NTVOxafOaic0HuXHLiuOp2JQZp8edYFR5PVw7WXH869vPprfX3Uqnzn3yEPGjBYCnzn3VTRVFvP//vAcEYc0gJ58pY9QJOqoflcy2psq2e6EhzIQSKnCy6apqpix8Hjas0n6MxSGtLGNUTp5FHtSYy7umEWE09saWL+tO6+zOabi3i0dnNxSl5HX7C/ycOKy2hkbHN1WJUiX5Y0VvOPExdy44ZV4ebwbpHJV+08R+Z6IfA8rZ/LlhOdfd21lcwyvR7jijOWcdERdvpeSlMoSH1956zFsOTDIL9fvcuRnrt/eg9cjnNzq7u9sjwPOplJtNBRhYCycckIeEgdtpRdGsIZrZZFDyUDC3u2mxsmc0d5A32iYLQcGZz44h+zuGeWljqGUuuOnYk1rPS8cHJzWoBeahwLwybPaMcbw/b85JnByGDMZlAeBFcCxsW09sCzh+YrYMcoc4PxXL+ANRzXx7XUvs8OBuSnrt3dz3JLqw6bgOU1bUwUjofF42W8m2O9NRcfLxr44p9PcOB41DAbCVDngoaQjYZ9roUK7eqrQ5OzXbbH09mYSg5yO1a11GAObphmy1zkUwO/1ZJUrc5oltWW8a/Uybtm4x7Xes2kNijHmTGPM62faXFmZknNErAR9sc/DP/3uKYKRzAvlhoMRntk74Hq4CywZe8guMW9PalxQlUbIK+ahpJPoHAqEMSYzHS8b+73pNDd2DgYp9XldN+42TZUlHLWgsuD6UdZt6eCoBZUsq89czuiEZTX4vZ5pGxztHpR8Ftwkw1bf+O79W135+YUVyFfyzoLqEv774uPYvH+Qb/4186qvjTt7GY8aVxPyNvFKryw65vfHelAy8VDSaW7MVscLJjrsB9LoK+iMDdbK5QXu9LYGNu7qy7ni7VT0joTYtKs3q3AXWC0Bxy2tTsmgFBrNVSW8/9QjuP3pffGbKCdRg6Icxjkrm/nAaS1c/8jOjOe8rN/ebSUwj0hNJykb6iuKqSv3ZzXe2P7jak5DHqayuIhSnzee8E6FuI5XFgaluMhLmd+bZg4l9012a9sbCEWibJwmNJRL/vZiJ1GTXbjLZk1rPc/vG5iyIKNQDQrAx85s448fPy2tfGGqqEFRkvL5Nx7F0Qur+Ozvn8noTmb99h5OWlabM6VVS9Mrc4OyfyBAfRpNjWCFCJuqitPqlo/reGUoDGlTU+pLS8K+MweyK5NZ01qH3+spmH6UdZsPsrC6hFcvTm1s9nSsWV7HeNTw5CvJZ7/kW8drOurK/a5pBapBUZJS4vPyg3efQCAc5Zqbn0pLK6tvJMSWA4M5CXfZtDVXsDWLSq+DA2MZ3bE1VRanFfIacMBDAWs4V7pVXrm+Yy7zF3HiEYUhZx8Ij/PQ1m7OPrrZkbDfictq8XokaT9KeDxK70ioYD0UN1GDokzJisYK/v3CY3hsRy8/eiD1UsMNO3swBsfnn0xHe1MFA2Nhuocz0ytKtwfFpqmqJK2kfDbDtRKx5FdS+11HQxGGg5GclQwnsratgc37B+kZdrdDeyYe3trNWHg8LTHI6SgvLuLYxdVJ+1G6hwunSz7XqEFRpuWSk5ZwwXGL+M79W6ctk0xk/fYeyvxe1yX4E5mQYMksMZ9ul7xNU2W6Ia/M58knUlueesjLzvE05+ECt7bdkv57JM9y9uu2HKSyuMhRTbk1y+t4Zm//YUUHhdiDkiuyMigicp+IuNvLr+QVEeHrF72axTWlfOqmpxlIIcyyfnsPq1vrcqoG0N5kiWBn0jFvNzUuTKPCy6apsoThYISRFLvl+8dCVBYXUZTluakuTT3kleumxkSOXVxNVUkRD2/NX/nweNRw/wudnHlUE/4i576Ta1rrCI8bntx9aB5lQpVADUq6bEQbG+c8lSU+vv+uE+gYDPAvtz07bZ6iczDAts7hnOZPAJqriqkoLsqoFyWdOSjJPhdSH7Q1MBbOeLBWIjVl1tTGVHJGE02NufdQvB7htBUNPLy1Oyslg0B4nM37BzIaWf3U7j56RkKcm2W58GRWtdThEQ4Le3UNz18PJasuJ2PMF5xaiFLYHLe0hs+dfyTfuOtFfrNhN+895Yikxz26wwpt5KKhMRERiUuwpMvBNCY1TmZCfiVAa0P5jMcPjGYnDGlTU+ojPG4pDs/UrJjvO+a17Q3cvfkgO7tHWJ6BIOrevlGuuGETLx4coszvZU1rHWvbG1nb1sCrmitmTLKv29KBzyuceaSzE1qrSnysXFR1mPKwfb4bKtSgKMqUXLF2OQ9v6+Grf97CqpZajlpwePnl+m09VJf6OHph9qWZ6dLeVMHfX04/tGI3NebCQ7GEIbOX8o/Lr4yGZjYoQ0H8Xo8jhiwT4nL227rTNigbd/Vy1a+fIDQe5StvXcmO7hEe3trNAy9tASwvYG1bA2vbGji9reGwSj1jDPdu6eCU5fVUljj/+69uqec3G14hGBmnuMgqOe8aDlBb5nM0vDZbSMmgiMj1U7xkgACwDbjZGLPfqYUphYfHI3z7kuN443cf4urfPsWfrl5Lqf/Qvo31O7o5ZXldynO6naStqYLfP7GXgdH0wkqZNDXa2B5KZ4qlw/2jIRYkMcTpkigQuWSG3tHOoUBeZUCOqC9naV0pD23t5v2ntqT8vls27uGLtz/Hktoyrrt81SHjHvb1j/HI1m4e2tbNgy938cenrInf7U0VnB4zMKesqOfgwBg7u0f40NpWp38twErMX//ITp7dO8DJLZYIaj56fgqFVD2URuAMIAo8H9v3aqyBW08Abwe+KiJnGGOednqRSuHQWFnMtZcdx/t+/jhf/fNm/vPtr4m/tqd3lD29Y1yxdnle1tZuT2/sGkpL1TmTpkabqtIi/EWe3OdQSlOXsC+Eru21bQ38+ZkDRMajMxYkRMaj/OdfX+TnD+/kjPYGfvCuEw87Z4trSrn05KVcevJSolHDCwcHeWRbNw9t7eZ3j+/ml+t3UeSR+E3COS6N117dMjFwyzYoXcP5P9/5IlWf7BHgr8ASY8xrjTGvBZYAdwHrgCOAvwDfdmWVSkFxRnsjV71uBb97fA9/eXZiFv2j2+38SW4T8jZtjValV7od8wcHxjKq8AIrd9NcVZySh2KMsaTrHVCgTUfCvmMw/7PN17Y1MhQTDJ2OwUCYD9+wiZ8/vJMPnNbCLz5w8owG2OMRjllUzZWvXcGvP7yGZ758Lr/9yBqufO1y6iv8XHDcIldkRgBqy/0c2VzJYzsmyqJzNWq5EEnVQ/kU8AZjTFzz2BgzKiJfB+43xnxLRL4J3OfGIpXC4zPnvorHdvTw+T88y2uWVLO0roz127tpqCiO94TkmsW1pZT4PGkn5g8MBFhSm7n6bFNlSUoeykhonEjUOJOUL7MVh2dubuwcCrLa5Zk0M3HainpErAbDk6bQd9vZPcIVN2zklZ5RvnHRsbx7zbKMPqvE5+W0FQ2ctqKBz2Wz6BRZs7yOW5/YS3g8SpFH1ENJgQpgYZL9C2KvAQyiSf55g8/r4fvvOgEMfPKmpwiPR1m/vSd24chPrN7rEVY0VqRdOnxgIJCWyvBkUpVfsTvbnUjKV6cY8gpGxukfDec9pl9b7ufYxdU8MoUMy8Nbu3nbDx+hdyTEjVesydiY5IM1rfWMhsbZvH+QwbEIoUhUDcoM/BH4uYhcIiItse0S4OfAH2LHrAZedmORSmGytK6Mb7z9WJ7a3c81Nz1N51Awb+Eum3RLhzOZ1DiZ5qrUPJR4l7wDHkqJz0upzzuj/Irdtd2ch6bGyZze1sCTu/sOUeg1xvCrR3dx+S8eZ0FVCXdevZZTluf3O5QuJ7daHteGHT10DVs3FmpQpucq4B7gRmB7bLsRuBv4eOyYF4CPOL1ApbB563GLuGzVUv7ynJVLyXX/yWTamyrY1z+Wcud6fFJjBj0oNo2VxQwFIoyFpp/7EReGdGiKX02Zb8YcysRs8/xXHZ3R1kAkatgQyzeEx6N88fbn+bc7NvP6Ixu57eOnsbQu89BjvmiqLGF5YzmP7+xN6PnJ//nOBykZFGPMqDHmKqAOOCG21RljPmaMGYkd87RWeM1PvnzBStqaKjiivoyldZlfmJ3Azt+kOhvlQH9sUmMWHoqdgJ1pFPDEcK3sQ15ghb1mmtpoX+AK4Y75pJZaSnweHtraTe9IiPdet4HfbtjNx85cwf+9b1XOpkm6wZrWeh7f1cvBwfntoaTah3IN8FtjTCfwrKsrUmYdZf4ibr7yFEZD43kfedoW0/Ta1jmckjjlgYHYpMYsPBS7NLVzKMgR9VN3y9sz4J1qMLTlV6ajy5ZdKYCQV3GRl9Wt9dy7pYO/vdjJwcEA1152HBedsCTfS8uaNa11/O7x3TwUm/1SCOc7H6Qa8vo0sFdE7haR94jI7PNLFVepryguiHDFEfVl+LyScmLeDnllcwGw3zvT5EY75JWt0rBNbQozUTqHgngE6ssL4wK3tq2eff1jjIXHufnKU+aEMQHiVXTrNh+kuMhD5Sz2trIhVYNyBHAesAf4PtAhIjeKyPkiMv/0BZSCxef10FJfnnIvyoEsmhptEvW8pmNgNEyJz+PYFMuaspkl7DsHgzRUFOdFuSAZF5+0lI+c0cqdV5/OCcvcHw+dKxbVlLK0rpSR0HheVQnyTao5FGOMecAY8xGsUuHLgRKsCq+9Lq5PUdKmvbki9RxKFk2NNrVlPnxembHSy2pqdCZ/ApaE/cBoeHr156FAQYVf6sr9fPHNKzMS4ix07Fkr87WpETKQrzfGhIBHY9srWAZGUQqGtsYKXukZOWzwUTIODgRYUJXdxU1EYs2NMyTlx0KOhbvA8lBC41FGp6kus2abz8+Ko1yzJhb2mq8JeUjDoIhIpYh8UETuA3YDVwC/BVa4tThFyYS25kqiBnb1jMx47P7+sayaGm0aK4tnzKH0pylaORO1tuLwNGGvjnksA5JrJjyU+WvAUzIoInIr0AH8J7AZOM0Yc7Qx5mvGmJ1uLlBR0qXdHgc8Qx5lJBhhMBBxROepuap4Rg9lYMwZHS+b6lJbzyt5pVdkPErPiBqUXLG0rpT3rFnGecfM36BNqqUIQeAdwDpjzCH+tYicbYxRDS+lYGhtKMcjzFjp5URTo01TZQkbJg1amkz/aJjXLHE25AVMOZa5ZySEMdCUgSy/kj7WuOxj872MvJKSQTHGvCfxuYgsBj4IfAirAsyZshVFcYASn5dldWUzzpe356A44aE0VRbTPxomEB6fsoqrfyzkWFMjJApEJjco+Z7UqMw/0smheEXk7SJyF7ALuAj4CdDm0toUJWPamirY2jk07TH7HWhqtLGbG7umqPQKhMcJhKPOJuXtkNcUzY3xWfLqoSg5YkaDIiJHish/A/uB/wGejL30PmPMtzSHohQibU2V7OweITIenfKY+KTG6uzv4BtnGAUc1/FyMCk/MQZ4Cg9lSD0UJbdMa1BE5CHgMaAWuNQYs9wY8685WZmiZEF7UwXhccMrvaNTHnNgIEBDhT8+Czwb4npeUzQ3xnW8HOxDKfF5KfF5ppSwt0NeDRVqUJTcMJOHcirwK+BaY8w/crAeRXGEthQqvQ4MjDk2yS9RzysZ8VkoDnooYBmoqaq8OocC1JX78RepmIWSG2b6pp2Mlbh/WESeEpF/FpH5WxOnzBpWpKA6fHAg4FjHdl2ZnyKPTFk67LSOl01N2dSKw1ZTo3onSu6Y1qAYY54yxnwCa1rj/wIXYOl5eYA3i4gjYjwiUici94rI1ti/SX+uiFweO2ariFyesP/vIvKSiDwd25qcWJcye6koLmJRdQlbO6ZOzO/vH2OhQx6KxyM0VBTTMUVzY78LORSwDNRUZcOdQ/N3FK2SH1LV8goYY35tjHk9cDTw38A/AwdF5K8OrOPzWLPp24H7Y88PQUTqgC8Da7CmQ355kuF5jzHm+NjW6cCalFlOW3Ml26bwUOymRic1pazmximS8g7PQrGpLfNPWeXVNRiY113bSu7JRMtrmzHm88BS4FJg+oEMqXEhcEPs8Q3A25Iccx5wrzGm1xjTB9wLnO/AZytzlPbYOOBo9HDxRLup0SkPBaCxsmTqpPxYCK9HKPc727I11dTGaNRYIa8CEoZU5j4ZZ+uMMePGmDuMMRc6sI5mY8yB2OODQHOSYxZjhdts9sb22fwiFu76kkyjHS0iV4rIJhHZ1NXVlfXClcKlramCQDjKvv6xw1476IJBmc5DsZSGfY7LmlfHJOwnKw73jYaIRI3mUJSckrPyDxG5T0SeT7IdYpCM9ZcxtR53ct5jjDkWOCO2vW+qA40xPzXGrDLGrGpsbEz791BmD7am17YkHfN2U6OTIa+myhJ6R0KEIof3vvSPOSsMaVNT6icUiTI2SVnZNmzN2tSo5JCcGRRjzNnGmFcn2e7AGti1ECD2b7IcyD6sMJvNktg+jDH2v0NYCsir3fxdlNlBvHQ4Sce8k02NNnZ4qWv4cC9lYNRZYUib2imaG7WpUckHhVKgfifW0C5i/96R5Jh7gHNFpDaWjD8XuEdEikSkAUBEfMBbgOdzsGalwKkp89NQUZzUQzkwMOZYU6NNc9XUzY1O63jZTNUtb69Bk/JKLikUg/JfwDkishU4O/YcEVklItcBGGN6ga8BG2PbV2P7irEMy7PA01hey89y/hsoBUlbU3lS1eEDDvag2NgX72R5lH6XPJTqKfS84h6KJuWVHJKqfL2rGGN6gLOS7N+ENcjLfn49cP2kY0aAk9xeozI7aW+q5Pan9mGMOSQhfqA/wLL6Mkc/azr5lQGHh2vZTOWhdA0FqSwpcmx+vaKkQqF4KIriCu3NFQwFI4d5DQcGxljkYIUXQH1FMR453EMJj0cZCkYc1fGymTLkNRTQ/ImSc9SgKHOatsbDNb0mJjU6G/LyxrrlJ48CHnSpSx6sxkZIEvIa1FnySu5Rg6LMadqa7dLhiUqv+KRGB2bJT6apqpiOSXpebkjX25T4vBQXeQ6TX9GmRiUfqEFR5jSNFcVUlRQdkpg/EOtBWeBCj0ZzZclhHkq/S8KQNpO75Y0xdAxqyEvJPWpQlDmNiNDeXDnJoNgeirMhL7A8lMk5FLd0vGxqSv30JUjYDwYiBCNRDXkpOUcNijLnaW+qOGS+/IF+ezSu83fwjZUl9IwED5kUaec33CgbhpiHkjBkq2vIvd9PUaZDDYoy52lrqqBnJETviHVhPzg4RkNFsaNNjTbNVcUYA93DEx6DHY5yM+SVmEOxQ27qoSi5Rg2KMudpm6Tptb8/4KgoZCITzY0TiXnboFS5ZVBKD5Ww16ZGJV+oQVHmPJM1vaxJjW4ZFOsinjhoa2AsTFVJEV6Ps0rDNvbURltx2DZmmpRXco0aFGXOs6i6lDK/N96Lsn/AuUmNk5mYLZ/oobij42VTXeYjFIkSCFt5m87BIKU+LxXFBSGEocwj1KAocx6PR2hrqmB71zDDwQhDgQgLXajwAmio8CPCIaXD/WNhV3pQbCY3N9o9KE7PXlGUmVCDoswL2hor2NoxzMH4HBR3PJQir4f6cv9hORS3EvIwUT1m52pUdkXJF2pQlHlBW3MFBwcD8bCXG02NNk2TmhsHxsKuh7wg0aCo7IqSH9SgKPMCW9ProW3dgDtNjTaTmxv7R0Ou9aAAcdHJ/lhzY9dgkEb1UJQ8oAZFmRe0N1cC8ODLXYC7JbVNlcV0xCTso1ET81BczKGUxzyUsTCjoQhDwYiWDCt5QctAlHnB0tpS/EUe9va519Ro01xVQvdwkPGoYSQUIWrca2qERA8lHA+1NWvIS8kD6qEo84Iir4flDeWAewl5m6bKYqIGekaCrut4AZT4PPiLPPSPhbSpUckralCUeYPd4Oi2QWm0u+UHg/FEuZs5FBGhptRH/0g4oalRPRQl92jIS5k35MqgNMe8g86hAD6vdc/mxvjfRCyByFCCjpd6KEruUYOizBvam6zEvFtNjTZNsZLkjsFgvFvdTQ8FrJBa/2iYzqEgfq/H1SIARZkKDXkp84ZjFlUhQjyX4haNFTEPZTA4MVzLbQ+l1MfAmBXyaqzULnklP6iHoswbWhrKuf/Tr6Ol3l2D4i/yUBfrlo9FvFyt8gIr5PXs3jBdQ9qDouQPNSjKvGJ5rMHRbaxeFEuksczvdbVMGayQV9+olUM5or7M1c9SlKnQkJeiuEBTVQldQwFLGNJl7wQsDyUYibKnb1RLhpW8oQZFUVygqdKSX+kfDVPtYg+Kjd3cOBoa15JhJW+oQVEUF2iqLKZrKEifyzpeNolVXVoyrOQLNSiK4gLNVSVEooZd3SM5KeFNNFrNLiopK8p0qEFRFBewvYSekVBODEpiWbJWeSn5Qg2KorhAYmK8utT9HEptQp5Gk/JKvlCDoigukJgYz0nIK/YZHoH6cjUoSn7QPhRFcYHEsJPbTY0ApT5vXHLF69EueSU/qIeiKC5Q4vPGDUkuqrxEhOoyn4a7lLyiBkVRXMJWHXZbx8umsaKYRdXuCl8qynRoyEtRXKKpsoSXO4bjTYduc+1lx1Pmd1fiRVGmQw2KoriEXTqcKyn5IxdU5uRzFGUqNOSlKC5hz0XJRVJeUQoB9VAUxSXeceJiqkt9lBfrn5kyPygID0VE6kTkXhHZGvu3dorj7haRfhH586T9rSKyQUS2icjNIpKboLWiTEN7cyUfO3NFvpehKDmjIAwK8HngfmNMO3B/7Hky/ht4X5L93wSuNca0AX3Ah11ZpaIoijIlhWJQLgRuiD2+AXhbsoOMMfcDQ4n7xJp1+gbg1pneryiKorhHoRiUZmPMgdjjg0BzGu+tB/qNMZHY873A4qkOFpErRWSTiGzq6urKbLWKoijKYeQsWygi9wELkrz0xcQnxhgjIsatdRhjfgr8FGDVqlWufY6iKMp8I2cGxRhz9lSviUiHiCw0xhwQkYVAZxo/ugeoEZGimJeyBNiX5XIVRVGUNCmUkNedwOWxx5cDd6T6RmOMAR4ALs7k/YqiKIozFIpB+S/gHBHZCpwde46IrBKR6+yDROQh4PfAWSKyV0TOi730L8CnRWQbVk7l5zldvaIoilIYjY3GmB7grCT7NwFXJDw/Y4r37wBWu7ZARVEUZUbEihjNT0SkC3glxx/bAHTn+DMLHT0nh6Pn5HD0nBxOvs7JEcaYxsk757VByQcisskYsyrf6ygk9Jwcjp6Tw9FzcjiFdk4KJYeiKIqizHLUoCiKoiiOoAYl9/w03wsoQPScHI6ek8PRc3I4BXVONIeiKIqiOIJ6KIqiKIojqEFRFEVRHEENiouIyC4ReU5EnhaRTbF9KQ0Tm0uIyPUi0ikizyfsS3oexOJ7sWFpz4rIiflbuXtMcU6+IiL7Yt+Xp0XkTQmvfSF2Tl5KUIiYU4jIUhF5QES2iMhmEflUbP+8/a5Mc04K8ruiBsV9Xm+MOT6hVjzVYWJziV8C50/aN9V5eCPQHtuuBH6cozXmml9y+DkBa1Dc8bHtLgARWQm8Ezgm9p4fiYg3ZyvNHRHgM8aYlcApwCdiv/t8/q5MdU6gAL8ralByT0rDxOYSxpgHgd5Ju6c6DxcCvzIWj2EpSS/MyUJzyBTnZCouBG4yxgSNMTuBbcxBqSFjzAFjzJOxx0PAC1izjebtd2WaczIVef2uqEFxFwOsE5EnROTK2L5shonNJaY6D4uBPQnHTTswbQ5ydSx8c31COHTenRMRaQFOADag3xXgsHMCBfhdUYPiLmuNMSdiueafEJHXJr4Yk96f93Xbeh7i/BhYARwPHAC+ndfV5AkRqQBuA64xxgwmvjZfvytJzklBflfUoLiIMWZf7N9O4I9YrmeH7ZZnMExsLjHVedgHLE04bt4MTDPGdBhjxo0xUeBnTIQq5s05EREf1oXzN8aYP8R2z+vvSrJzUqjfFTUoLiEi5SJSaT8GzgWeJ4thYnOMqc7DncD7YxU8pwADCeGOOc2k+P9FWN8XsM7JO0WkWERasZLQj+d6fW4jIoI1y+gFY8z/Jrw0b78rU52Tgv2uGGN0c2EDlgPPxLbNwBdj++uxKlW2AvcBdfleaw7Oxe+w3PIwVkz3w1OdB0CAHwLbgeeAVflefw7Pya9jv/OzWBeGhQnHfzF2Tl4C3pjv9bt0TtZihbOeBZ6ObW+az9+Vac5JQX5XVHpFURRFcQQNeSmKoiiOoAZFURRFcQQ1KIqiKIojqEFRFEVRHEENiqIoiuIIalAUJQ+IyAdEZDjf61AUJ9GyYUVxGBGZ6Y/qBuBjQKWxVBQUZU5QlO8FKMocJLGL+S1Y0hiJ+8aMMWPAWE5XpSguoyEvRXEYY8xBewP6J+8zxgxMDnnFBiY9LyKXizWYbUREfiEifhH5uIjsEZEeEflfEfEkvM8vIt8Ukb0iMioiG+fqAC6l8FEPRVEKhxaseRZvwZIcvw3LszmApQV3FHAL8EjsNYBfYKnOvhtLwuVNwJ9E5GRjzDO5XLyiqEFRlMLBC3zQGDMAPC8idwOvAxYbY0LACyLyCPB64DYRWQG8C2gxxuyO/YwfiMjZwEeBj+f+V1DmM2pQFKVw2B0zJjYdwMsxY5K4ryn2+EQsgcQtlihtnGLgb24uVFGSoQZFUQqH8KTnZop99oxwT+z5yUmO04S/knPUoCjK7OUpLA9lgTHmgXwvRlHUoCjKLMUY87KI/Ab4pYh8BngSqAPOBHaYiYmHipIT1KAoyuzmg1gDlb6FNe61F2tCn3osSs7RTnlFURTFEbSxUVEURXEENSiKoiiKI6hBURRFURxBDYqiKIriCGpQFEVRFEdQg6IoiqI4ghoURVEUxRHUoCiKoiiO8P8D9MDKwcuORUwAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plt.plot(header,values.mean(axis=0))\n",
"plt.xlabel(\"Time\",size=14)\n",
"plt.ylabel(\"Avg. Expression\",size=14);"
]
},
{
"cell_type": "code",
"execution_count": 69,
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 69,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAY4AAAEKCAYAAAAFJbKyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8/fFQqAAAACXBIWXMAAAsTAAALEwEAmpwYAABhBElEQVR4nO2deXhU1dnAf2eyb2RPgIRsEPadgCCgqKhgVdxw36vWqv3aqm1dqrW2ttZaa21xrVZxR1xARUUBRWQz7EtWIIQQyL7vyZzvjzMTkjBJZjIzmZlwfs8zz8zce+feNzcz973vLqSUaDQajUZjLQZXC6DRaDQaz0IrDo1Go9HYhFYcGo1Go7EJrTg0Go1GYxNacWg0Go3GJrxdLYCziYqKkklJSa4WQ6PRaDyKbdu2lUopoy2tG/CKIykpifT0dFeLodFoNB6FEOJwd+u0q0qj0Wg0NqEVh0aj0WhsQisOjUaj0diEVhwajUajsQmtODQajUZjE1pxaDQajcYmtOLQaDQajU1oxdENRqPkL6syOFJe72pRNBqNxq3QiqMb8srqeG9rPouW/MCPeeWuFkej0WjcBq04uiElOphP7p5NaIAP176ymQ/Sj7haJI1Go3EL3EpxCCEWCCGyhBC5QogHLKy/UwixRwixUwixQQgx1pnypEQH88lds5mRHMFvlu/mr6syaDPqiYkajebUxm0UhxDCC1gCLATGAtdYUAzvSCknSCknA08BzzhbrtBAH16/ZQbXz0zgpfUH+dmb6dQ2tTr7sBqNZqBhbIPSHFdL4RDcRnEAM4BcKeVBKWUz8B6wqOMGUsrqDm+DgH65/ffxMvDnSybw+KJxrMsq4YoXNuqguUajsY3d78OS06C60NWS2I07KY44oGMgocC0rBNCiLuFEAdQFsf/WdqREOIOIUS6ECK9pKTEYQLeOCuJ12+ZztHKBi5Z8gPpOmiu0Wis5dgukG1QvN/VktiNOykOq5BSLpFSDgd+B/y+m21ellKmSSnToqMttpPvM3NTo/n4rtmE+Htz7StbWL6twKH712g0A5SSTPVcdsC1cjgAd1IcR4FhHd7Hm5Z1x3vAJc4UqDtGxKiMq2mJ4dz/wS6e/CITow6aazSanijJVs8DIM7hTorjRyBVCJEshPAFrgZWdtxACJHa4e1PAJf9B8ICfVn60xlce1oCL353gJ+9tY06HTTXaDSWaKyCGlNsoyzXtbI4ALdRHFLKVuAe4CsgA1gmpdwnhHhcCHGxabN7hBD7hBA7gXuBm1wjrcLHy8ATl4znsYvGsiajiMtf2EhBhQ6aazSaLpitDf/QAaE43Gp0rJRyFbCqy7JHO7z+Zb8L1QtCCG6enUxydDD3vLOdS5b8wEs3pDEtMdzVomk0GnehNEs9j1ygsqtaGsAnwLUy2YHbWByezpkjVdA8yM+ba17ezP7C6t4/pNFoTg1KMsHLF0bMV+89PECuFYcDGRETzEc/Px1fbwMvrffsL4ZGo3EgJdkQmQrRo9R7D3dXacXhYCKD/bh6+jA+232Mo5UNrhZHo9G4AyWZSmlEjlDvyzw7s0orDidwy5xkAF7/4ZCLJdFoNC6nuR4q85Xi8A2CQXHaVaU5mbiwAH4yYQjvbj1CdWOLq8XRaDSupCwHkCfcVJHDPb6WQysOJ3H73BRqm1p5f6tux67RnNKYU3GjzIojVSkT6blFw1pxOIkJ8aGclhzB/344REub0dXiaDQaV1GSCcJLWRqg4hyNVVBf5lq57EArDidyxxkpFFY1smrPMVeLotFoXEVpFkQkg7efeh9laoDhwZlVWnE4kbNGxZASHcQr3x9EerBZqtFo7KAkC6JHn3hvtjw8OM6hFYcTMRgEt89NYe/RajYf1C3YNZpTjtZmKD8IUSNPLAtLBIOPtjg03XPplDgig3x55fuDrhZFo9H0N+UHwdja2eIweEFEilYcmu7x9/HihlmJrM0sJre4xtXiaDSa/sTcoyp6ZOflUalacWh65oaZifh5G/jv97ogUKNxK+pKwejErMcSk+KI6qI4IoebrJE25x3biWjF0Q9EBvtx+bR4PtpxlJKaJleLo9FoAOrL4dmJsP115x2jJAtCE1TFeEciU6GtGSoPO+/YTkQrjn7ip3OSaW418uZmz/yiaDQDjoIfoaUODn3vvGOUZJ2oGO9Ie88qz2w9ohVHPzE8Opj5Y2J5c1MeDc2eaZ5qNAOK/M3q+Wi6c/ZvbFMV4pYUh7mWw0NTcrXi6Edun5tMRX0LH24vcLUoGo3myFb1XJkPtSWO33/lYWhttKw4AiM9ehqgVhz9yIzkCCbFh/LqhkMYjbogUKNxGW0tcHQbDJ6o3hdud/wxuvao6ogQJ3pWeSBacfQjQghum5vCodI6vskocrU4Gs2py/Hd0NoAp92p+kgVOMFdVZKpnrum4pqJHKFjHBrrWDh+MHFhATo1V6NxJflb1HPKPIgZq6wPR1OSBcGDISDc8vqoEVB9FJrrHH9sJ+NWikMIsUAIkSWEyBVCPGBh/b1CiP1CiN1CiDVCiERXyGkP3l4Gbp2TzNa8cnYeqXS1OBrNqcmRLRA6DELjIG6qUhyO7idXmtW9tQHKVQUeaXW4jeIQQngBS4CFwFjgGiHE2C6b7QDSpJQTgeXAU/0rpWO4avowQvy9dRsSjcYVSKkUx7DT1Pu4adBYqQryHHmMkuzOrUa64sFjZN1GcQAzgFwp5UEpZTPwHrCo4wZSynVSynrT281AfD/L6BCC/by5dkYCX+w5xpHy+t4/oNFoHEfVEag5dkJxxKepZ0e6q6oLobnm5Irxjpi75GqLwy7igI7j8gpMy7rjp8AXTpXIidw8OwmDELym55JrNP2LOQ03waQ4okeDT5BjFUd7YLwHi8MnQLnLPLCWw50Uh9UIIa4H0oC/d7P+DiFEuhAivaTECfnZDmBIaAAXTRrKsh+PUNWg55JrNP1G/malKGLGqfcGLxg62bGZVaWmVFxLNRwdiRzhkbUc7qQ4jgLDOryPNy3rhBBiPvAwcLGU0mLjJynly1LKNCllWnR0tFOEdQS3zU2mrrmNd7fmu1oUjebU4cgWiJ8GXt4nlsVNNaXoNjvmGCWZKpsqqJfrj1lxeNigN3dSHD8CqUKIZCGEL3A1sLLjBkKIKcBLKKVR7AIZHcq4oaHMHhHJ/344RHOrnkuu0Tidphoo2gvDZnZeHpemmg4W7XXMcUqyVeGfED1vF5UKTdVQ556eke5wG8UhpWwF7gG+AjKAZVLKfUKIx4UQF5s2+zsQDHwghNgphFjZze48htvmplBU3cRnuwtdLYpGM/A5ug2k8URg3EzctBPrHUFJZu9uKvDYMbLevW/Sf0gpVwGruix7tMPr+f0ulJOZNzKa1JhgXl5/kEunxCF6u0PRaDR9J38LIE5kUpkJjYegGJPiuN2+Y9SVQkO5lYrDXMuRC0mz7TtuP+I2FsepihBqLnnm8Rp+yC1ztTgazcDmyBaIGQMBYZ2XC5MycYTF0Z5RZYXiCI0HLz+Pq+XQisMNWDRlKFHBfrogUKNxJkajmsHR1U1lJm6qyoZqqLTvOO1T/6xQHAYv5a7ysFoOrTjcAD9vL24+PZHvskvIOq7nkms0TqEkQwWiu1UcpjhH4Q47j5MFvsHKmrCGyOEeF+PQisNNuO60RPx9DPxXWx0ajXM4YmpsmNCN4hg6VT3b664qzVLZUtbGKyNToeKQavXuIWjF4SaEB/lyZdowVuwspLi60dXiaPqB+5btYln6kd431DiG/C2qriI82fL6gDB1EbdXcZRk9Vwx3pXIEWBsVQOlPAStONyIW2cn02I08samPFeLonEyjS1tfLyjgC/3Hne1KKcO5saGPVkCcdNUBXlfC/Iaq1QfrJ56VHXFA8fIWqU4hBD+QojfCSFWm+ondnd8OFvIU4WkqCDOGxvLW5vzqW9udbU4GidysKQOo4S8Us+bxeCR1BYrd1B38Q0z8WlQV6zmZPQF89Q/Wy0O8KjWI9ZaHM8DDwB5wCfAh10eGgdxxxkpVDW08EG6nks+kMkpVkkQ+eX1tLbprgFOpz2+MbPn7eLsjHOUmjKqrEnFNRMYAQERHpWSa20B4CXAYinlN06URQNMS4xgSkIYr244xPUzE/Ey6ILAgUhucS0ArUbJ0coGEiODXCxRN2R8Bp/9Gu7eoi5wnkr+ZlUvMWRSz9vFjgcvX+WuGruo520tUZKpjhNm44y5qFSPSsm11uKop3PLc40TuWNuCvnl9Xy9X/u/Byo5RbXtrvZD7uyu2vhv5brJ3+RqSezjyFYYOgW8/XreztsPBk+Eo9v7dpySbKUEvGxsyhE5YuDFOFCT9u4Vuh9Gv3DeuMEkRATy8nqdmjtQySmuYfKwMMCN4xwlWXBks3rtyYqjpRGO7YRhM6zbPm6aquUwttl+rJJM2wLjZiJHQO1x1YTRA7BWcZwLXAXkCSG+EEKs7PhwonynJF4Gwa2zk9ieX8m2w+WuFkfjYJpbjeSV1XP68EiCfL3IK3PTKZDbl4LBR1VA5292tTR959hO1fm2t8C4mbhp0FJ3onWItTTXq5RaWwLjZjwsQG6t4igFPgbWAseBsi4PjYNZnDaM0AAfXlmvJwQONPLK6mgzSkbGhpAYGURemRtaHK1NsPMdGH0BjFoIhTvVhdETMQfGbVEcYHuAvCwHkBDdB4vDnJLrIXEOqxxxUspbnC2IpjNBft5cd1oCL3x3gMNlde4bPNXYTE6RCoyPiAkmOSqIfYVVLpbIApmfqQ6vU29SFc0/PAuF2yFpjqsls538LRCRAsFWDnWLHA7+oUpxTL3R+uOYe1T1xeIITwaEx8Q5bCoAFEKkCCEuFEL8RAiR4iyhNIqbT0/C2yB4bYO2OgYSOcU1CAHDo4NJigrkSEUDLe6Wkrt9KYQmQMpZJ2IDnhjnkNJU+NdLGm5HhDAVAtpocZRkgfCCiOG2fQ7Axx/CEgaWq0oIMUgI8QGQi6rjWAHkCCGWCSFCnCjfKU3MIH8WTY5jWXoBlfUOGmmpcTk5xbUkRATi7+NFUmQQbUZJQUWDq8U6QfkhOPgtTL0BDAaVhhs9Bg57oOIoPwj1pdYHxs3ETYPi/dBsgxuxJFNZNt6+th3LTOQIj6nlsNbi+BcwETgLCDA9zjEte9YpkmkAuH1uCg0tbby9xXP62Gh6JreoltSYYACSo5QL0q0yq3a8CcIAk687sSxxlkpp7UumkSuxtvCvK3FpINvgmA2NMUqzbSv864q5lsMD5o9bqzguBm6TUn4npWwxPb4F7kAVB2qcxKjBIZwxMprXN+bR1OphP1ozTTXw3BTY+5GrJXE5LW1GDpbWMiJGGerm2JXb1HK0tcKOtyH1PAiNO7E8YRY010DRPtfJ1hfyN6t4hTWzMTrSXkGebt32rc3qom+P4ogcAc21UOP+9VvWKo4ALGdPlQP+jhNHY4nb5yZTUtPEip0eOpf8wFrlMvjmD+oHdgpzuKyeljbZbnFEBfsS7OftPplVOatVPUHXoLD5jt3T0nKPbIX4GcrlZgvBMSrGY21mVflBZaHYqqA64kEpudaezR+APwkhAs0LhBBBwB+Bjc4QTHOCOSOiGD04hP9+fxDpAWbsSWSvVkHDynzY9Y6rpXEpuaYeVSNjlcUhhCApKtB9LI7tb0DwYEg9v/Py0GEwKM6zAuQNFWp4k7VpuF2Jn2a94rBlXGx3tCsO949zWKs4fg3MBI4KIb4TQnyHakFyGvArJ8mmMWGeS55dVMt32SWuFsc2jEbI+Ur1/YlLg/VPu63VsTG3lGe/yXbqMcypuMNjTqRXJ7lLLUfVUWVxTLnu5JYZQiirI3+Tc33wXz4EH97mmGMUmNxM3Q1u6o24aepmp9aK31yp6XtjrsfoC4PiwDvAI2o5rFIcUsq9QCrwWyDd9PgtkCqldJjTUwixQAiRJYTIFUI8YGH9GUKI7UKIViHEFY46ridw0aShxA7y47/fe1hq7rEdUFcCI8+Hsx6EqiMq+OqGvPvjEf61JofaJue1tM8priU+PIBA3xMX5uSoII5WNNDc6uKU3J1vgzTClBssr0+YpWZNOGvgUGuzsnj2fAA5X9u/vyNblKVrLuizFVsKAUsyVTqtrx31VgaDx4yRtdrxJ6Wsl1K+IqW8z/T4r5TSYTmEQggvYAmwEBgLXCOEGNtls3zgZuCU83f4ehu4+fRkNuSWumfBWHdkrwYEjDgXhp+j/M3f/0NVJrsZh0prkRL2HnXe+c0pPpFRZSYpMgijVC3WXYbRCNvfhOQzIaKbCXnOjnMc/kEFh739YfXD9o9Szd8Mgyf0/WI+ZJJSPFYpjmz74htmPCQlt1vFIYS4TAjh0+F1tw8HyTIDyJVSHpRSNgPvAZ36Gksp86SUuwE3q5bqH66dkUCgrxevepLVkfMVxE+HoEjl7jjrQTUkZ/tSV0vWCSklh0qUu2hPgXMUR5tRcqCkltTYzqVPSe6QkntwHVTlw7Sbut8mZiz4DXJenCNntVIai5Yo10/6//q+r7ZWdcHva3wDlMKJGdt7ZpWxzf5UXDNRqVBx2G3duWZ6sjiWA+EdXnf3+MBBssTRuXV7gWmZzQgh7hBCpAsh0ktKPCwm0AOhgT5cNX0YK3cVcqzKjQrGuqOmSHUZHXneiWUpZ6kq3u+fUV1L3YSSmibqmlW6824nWRxHyutpbjUyoovF0V7L4co4x/Y31DCh0Rd2v43BSxXSOcviyP4SkubC+Msh+Qz49i8qwN0XivZAS73thX9diZuqFFBPMZfKw9DW5BjFETlCZWdV5Nm/LyfSreKQUhqklMUdXnf38Oo/ca1DSvmylDJNSpkWHW1lfxoP4dbZyRil5PWNea4WpXdyTX7qjhk6ZqujplBdrNyEg6a7/dAAH/YUVDrlGDmm4U1dXVXhgT4M8vd2XWZVbQlkroLJ1/Y+ryJhpspUqndw1+bSXJXSOvJ89R05/69qfvd3T/Vtf0e2qmdbC/+6Ep+m5CjvYcSBPT2quhJpbnbo3im5NiY3O5WjwLAO7+NNyzQdGBYRyMIJQ3hnS75Tg7gOIftLCBmq/MwdST4TEk43WR3uYTmZL9oXTBhCXlk9VfV2+tctYB4X29XiEEKQHOXCzKpd74CxxbqGfgmz1LO5IttRZH+pnkeabjIGj1dB+q0v9y1YnL9ZZSmFxtsnlzlAXtCDu8qsOPoyh6MrkaY+V24e57C2V9WVQojzOrx/VAhRIIT4SggxxEGy/AikCiGShRC+wNWAnvVhgdvnplDT2MqyH+0YytjS4NyLdmszHPgWUs+FrvO/hICzHlKFZtted54MNnCotA5fbwPnj4sFYK8TEhByi2oZEupPiL/PSeuSooLIK3VecLygop6z//EtB0pqO6+QUsWbhs20ztUSN03N6HB0nCP7SxVPCEs4sezs36v01NWP2L6/I1vti2+YiR4NPkE9B8hLslTtS0CY/ccLCIOg6AFjcTxmfiGEmAo8BDwH+AD/cIQgUspW4B7gKyADWCal3CeEeFwIcbHp2NOFEAXAYuAlIYSH9T9wDJOHhTE9KZxXNxyita9dVd+7Ft5e7FjBOpK/UbWoGLnA8vrkucqfveGfbmF1HCypIykysH0q324nBMhzimtPsjbMJEUGUVjVQGOLc9rKbMwt42BJHat2H+u84vBGdZHqKSjeEZ8ANYLVkXGOxiqliEae33l5cAyccR9kfwEH1lm/v6oCqC5wjOIweMHQyT0rjtIsx8Q3zESOUK47N8ZaxZEImOwxLgU+kVI+BdyLanboEKSUq6SUI6WUw6WUT5iWPSqlXGl6/aOUMl5KGSSljJRSjnPUsT2N2+emcLSygS/39aGvTVWBagOS971KI3QG2avByw9Szux+m3kPQm0RpL/mHBls4FBpLclRQYQF+pIQEcieo5UO3b/RKMktriU1xnIz6eSoINUB3EkpufuPVQPwfW5p5xXb31CZUmMvsX5nCTPVTG5HKfwDa8HYenK1OsBpP4ewRPjqIZUpZQ3tjQ0doDhAWVnHd1tOIZdS/YYcrTgGiMXRCJi/8ecA35heV3VYrulH5o+JJTkqiFfW96ENyd4P1bMwwM63HC8cqDTcpDk959AnzVbZMxv+aVv76t5oqoG8H6zevLXNSH55PclRyhqYEB/qcIvjaGUDDS1tpMZ2Y3FEObfZobn2Z0d+BXXm2FhDBexfARMWg29gD5/uQsIsFRMp3OEY4bJXQ0C4Stvuio8/nPu4anG+w8oU7iNbwScQYsc7Rr64aWr0bNHek9dVFyrL2tGKo65YWWJuirWK43vgH0KIR4A0YJVp+Ug6p9Bq+gmDQfDTOcnsKqjixzwbUxb3LFftP0YugF3vWX8nZy1lB9QdU1fXgyXmPaQqy3981THHbqiENy6C1y8wFR/2ztHKBlraJCmmi/fEuFAKKhoor3NcLn1uNxlVZpIjnZeSazRKMo7VMCImmJY2yZZDpn6luz+A1kbr3VRmzC4gR8Q5jEZVvzFi/sltTsyMXaSSKdY+Yd3FNH+zuth7nRxL6hPtFeTbT15n7lHliOI/M1Hun1llreK4B2gGrgDulFKa27QuRMUkNC7g8qnxhAf68PL6HlIFu1KSpczuCYvVvIXaIsj9pvfP2UKO6YKdel7P24Ga85AyD374l/1WR0MFvHkJHN+rsrm+etCqQipzKm5ytElxxIcBsMeB9RzdZVSZCQ30ITzQh0NOCJDnl9dT29TKDTMT8fM2sD671BQUfwOGTFYV0rYQFKkulI6IcxRuV4OWuouFgUqmWPAXqC9TXQd6orkOju9xTHzDTGg8BMdazqwy96hyRCquGXOzQzeOc1jbq6pASnmRlHKSlPK1Dst/JaX8P+eJp+mJAF8vrpqewLqsYusnBO5ZrlxU4y5VFkFQtON7R2V/qVITu2td0ZV5D6mLx9ZX+n7Mhgp481KlNK56Cy5+Tt2xbXmx14+aK8bNhXjj4wYBOLSeI6eolugQP8ICTdPhpIR3r1VuOhMqs8rxFse+QhXfmJIQxmkpkWzILVV3z0V7bbc2zCTMVLO8jXY2ccj+UrX1GH52z9sNnQKTroHNL6gJhd1xdJsqoLO3fqMj5lGylgLkJZnKzRYU5bjjhSer36inWxxCiGghRHSH9xOEEH8WQlzjPNE01nD+uFjajNK6rrlSwt7lKq4QEqtM+YlXqR9vXWnvn7cGc3zBGjeVmYTTVB+rjc9BU23v23eloQKWXqKGDF31FoxaoNKAU89XBWQ1RT1+/FBpHSH+3kQGqYt6iL8PKdFBDo1znNSj6thOyPoc1v65fThSspO65O4/VoWXQTAyNoS5I6LILa6lfvOrKg4wvo+9QhNmQVOVKga0h+yvlHUQGNH7tuc8CgZv+PrR7rcxB8bj0+yTqytxU1VtRUNl5+UlWcra6Jpybg/eviohwI1rOax1VS0DLgIQQkQB61HZVS8KIe5zkmwaK5gUH0ZUsC9rMop737hwu6qAndAhDXfK9SqjZff7jhHo4LcqcGopQ6YnznpIuSK2vmzb58xKo3j/CaVhZsFflQ9/zeM97uJQaR0pUUGIDj/+iXGhDnNVSWnOqOqgOHa9D16+ajrdp78Eo5HEyCCOVTXS0OzYlNx9hdWkxgTj7+PFnNQogmjAN+MjGHcZ+A/q207bGx7aEeeoLlRuU2tvMgYNgTm/hoyVkLfB8jb5W9R89IBwy+v7SpxJERV2iHNIqSwORxT+dSUq1fMtDtRscbND8wpUM8JxwI3Az5whmMY6DAbBWaNi+DarmJbeajr2LFcXq479iGLGKDN8x9uOmYGQ/RX4hdruKohPUx10Nz4HjdXWfaar0uh6AYocDjN/rjLHesjDP1Ra1+6mMjMhPoxjVY0U19jfT+tYVSO1Ta0nmhu2tajW4aMWwvl/gYIfIf1VkqJUZtPhcsdaHfsLqxk7RCmI0YNDuDowHe+2hr67qQDCk1TRmz1xjmxTeNQW63TWPTAoHr588OT550YjFGy1vz+VJYZOUc8dv0d1peo76Mj4hpnIESrJxF5XoJOwZXSs2YcwnxMV3dvp3CZE4wLOGRNDdWMr6T1lVxnbVBpu6nknV7hOvg6K99mfXimlmqMw/Ky+ZbTMe1D9ELe+1Pu2DRWwdJFJabzd/cXnjN9AUAx88TuLP8LGljaOVja0p+KamRgfCjimxfpJPapy16iYzqRrlKsw+UxY8zipAWo7R8Y5SmqaKK5pYuxQpTiEENzo+y0HiMc41A53jnmw02E7LI6c1apS3JYLr28gzH9MWSq73u28rjRLZV05Mr5hJiBM9ZHqmFlVau5R5QSLI3KEatJYc6z3bV2AtYojB7hMCDEMOA8w5znGApVOkEtjA3NSo/H1MrA2swdfft4GlUHV0U1lZvzlqp31DjtrOo7tUm1EbLmD7Ej8NOXi2vifntMu68tNSiPDpDR6yN7yH6QuNAU/wp5lJ602xxTMGVVmxg4ZhEE4poI8p0hlVLVbHLvehcBIlYIqBFz4T2hrJnX7nwEcmlllLvwzKw6O7yWxMYO3W84is6gP8aSOJMxSFdqVfcjIb2lUbs2RC2yPD0y4QtV8rHm8c0zMHN9wZEZVR+LTVGaV2TJvHxfrBIujPSXXPeMc1iqOPwJ/A/KAzVJKc4ez8wEHVQFp+kqwnzenpUT0HOfY8wH4hli+qAeEwZiLVeDcnmrg7K9oH9rUV856EBorYUs3Vkd9uUq5tUZpmJl0jXLHff0HFbzvgDmjKqWLqyrIz5sRMcEOmc2RW1xLZJAvEUG+ylLK+kIpcLNVFjkczvgNPlkruSRwt0MtDnPh37ghyoJi+1Kkly8ftc1hQ66dIwfsGeyUt0HdUdsaC4MT3XNrizplpXFkKwRGQUSK7fu0hrhpqjCvqkC9L8kG32DVTNHRtM8fd884h7XpuB8BCajiv44J19+g2o5oXMz8MbEcLK3jYNcmdqBaJexfCWMuVL2GLDHlOnWXn/l534XI+Ur9uILtaGU/dAqMugA2/efkDJZ2SyMTrn7HOqUBaiTnwqeUNdSlDuCQyeJIijq5wn1CXBi7Cqpsr8zvQqceVfs+UbMbJl3deaPT/w+ix/Awr1FY4qAMN1R8Iy4sgNBAH3VTsPs9xJiLiY4Zwvc5dh4ndry6GelLgDz7S5XVlTSnb8ceNl0p303/OWHx5G9W1oYjM5w6EjdVPZvjHObAuDOOFzJENVcszeVoZQNf7+85M7C/sWV0bJGUcgcQLYQwmJZtkVJmOk06jdWcPToGgLWZFqyO3G9U6uSEHlIvk86A0IS+u6tqS5T/t69uqo7Me0Apsc0vnFhmVholWUpppNpo1cSnKctj0xIVdDRxqKSOmBA/gv1OrlqeGB9KaW0Tx6v7HiCXUpJTVHOi1ciu95RrY8jkzht6+8JF/yLaWMzCEgdV0aMUxzizm2r/SnVep97InNQoth4qt6+pope3uoDbanFIqW4yUuapliJ95Zw/qOdvHlOB6vIDzgmMm4mdoJJLzBMBHTX1zxJCQORwZGkOdyxN5/al6SxZ5z7Wh7V1HD5CiKeEEDWoGRlJpuV/E0Lc5UT5NFYyLCKQUbEhlt1Vez5QJnzyvO53YDCoQT4Hv4XKfNsFyP0akNZVi/fGkEkq82vz88q1c5LSmN+3/c5/TP3wV/++fZGljCozE0wBcnviHCU1TVQ3tqrmhuUH4chmZW1YuktNOI09Qy7nqrbPacjrZVypFdQ1tXKorI5xQ81uqjdUcVnSXOamRtHUauw5ocIaEmapBAVbJvWVZKrvmL03GWHDlKW2d7myPMA5gXEz3r4weKK6QWqsUoFrZykOgKhUagsz2VdYzYS4UP7+VRYvfneg98/1A9ZaHH9A1XFcD3RsEbkVuNnBMmn6yDljYvgxr5yqhg5DiJpqlE993KXd9wIyM/laQMLOd3vezhLZX6n0TFvbV3THvAegqRrW/cUxSgMgZDCccT9krWpvs3KotI6UaMuKY+yQQXgZhF1xjk4ZVbveBwRMuLLb7Y9O+y1lhMJnv7K7h1jm8WqkNAXGc76Bwz+oYU0GA6clR+LjJfjeIXEOCUd+tP4z5qFNjrjJmP1L9b3b8E91U9DVknM0cdNU9mHRfvXeGYFxE/UhSQQ2HOXM4SF8fNfpXDRpKE9+kcnL612vPKxVHNegelStADrmNO5FNTrUuAHnjImh1ShZ37GKPHOVKoKzlE3VlfBElRq6823b8sfbWlRrbEtDm/rK4Akw5iJVEFiSBdfYqTTMzLxLBU+/fJCqmnrK6pq7tTj8fbwYGRti1wxyc0bViJgglU2VciaEdh9MjR8yhMdabiSgdI91ack9YG41Mr38M3jnSogZB9NuBlTwf2pCOBvsjXPETVPV3LbEObJXqzv3QUPtOzaAX7CqKAelNOxxfVlD3DQV1M8wVSQ4o/jPxMf5gXgheXxuMN5eBv555SR+MnEIf1mVyX+/t6E/nROwVnEMBQ5bWO5temjcgMnDwokI8mVNRodA2p4PVOzCWt/vlOuh8jAc7qYy1xL5m5R14Ij4RkfOfkRZMNe8o1JXHYG3nyq6K82mdsPzACfVcHRkYlwoewoq+xwgzymuJTTAh+iKHeq8Tuq5S09SVBCrjKeRFzFHdYPtS6qriYyjlfze/wPCvrlXxRNu/bJTa4+5qVHsK6ymrNbCnAlr8Q1S/yNr4xz15cpd11NTQ1uZdI3KCpx8reP22R3mVia7l6l5M+FJTjnMtsPlvHdQzX9PlGqCtreXgX9dNZkLJgzmz59n8NqGHnp2ORlrFcc+4AwLy68EehiNpelPvAyCeaOiWZdVoiYD1pUqS2DC5dZbAmMuUpXfO962/sDZX6lxoinz+iR3t0SPgp+td5zSMDNyAQw/h5ht/ySSqm4tDlBxjor6Fgoq+pambO5RJXa9p7JkOlbtWyDYz5voEH/ejvw/QMKq+/tW0d/SyILsR7iNj2HqTXDt+ye1F5mTqrLffjhQZvv+O5IwS2UaWRp01JUDa0EaHXuTYTDAVW9C2i2O22d3RKSoNjH1parWwuDl8EO0thl55JN91IckqQUdUnK9vQz86+opLBg3mMc/288bG/McfnxrsKWO499CiIcBL2CxEOJ/wAPAn5wlnMZ25o+Jpaqhhe35lbDvY9Up1Bo3lRmfABh/mRrwY+0gmZzVKq3Sz0NmegkBC57E0NbAb3yWkRDR/RAjcwV5X/tW5RbXMibaR6Xhjr1YuVZ6ITkyiJ01IXDWwyoesH+FbQetL8e4dBFnNq9nbfxdcNG/LFbyT4gLJTTAhw05DohztDVB4c7et83+UiVqDJ1q3zFdhblTLjgtMP72lnz2H6vmvovSVDv3Lu3VfbwMPHfNFM4dG8sfVu7jzU15TpGjJ6yt4/gUZV2ch4px/AFIBS6SUjp4mIPGHuamRuHjJZS7au+HquFbrI0TdqfcAK0NsPej3rctP6TSEh3tpnI20SP5LvRSrvT6Ft/iXd1uNmpwCD5eok+ZVWW1TZTXNXOW2KbSobvWbnRDUlSgqh4/7U7lBvrid9Yr8bID8N/5ULiDe5p/QfW0e7q1Nr0MgtOHR7Ihp9S+WpVh5kLAjT1v19aqkhJSz1NWgqdibnjoyOFNJkpqmnh6dRZzU6NYOH6wanNioQjQ19vAkmunMn9MDI+s2MfbWyxFEpxHr/89cyoukCmlPFNKGSylDJRSzpFSWjdiTdNvhPj7cFpyJHv271Wxh55qN7ojbqpSODutcFfZMrTJzXiRK6g1hMIXD3TrDvLz9mL04EF9mkFuzqiaVPalqi5OmmvV55KigiitbaKmRSproa4Yvvlj7x/M3wKvngsNFayf+V8+M846UcPRDXNSoyisauRAiR3V6sHRqtK5tzhHwY8qbdfTbjK6Yo5zOMHiePKLTBpb2njs4nGqW3Pk8G7bjvh6G1hy3VTOHh3Dwx/v5d2tfUij7yO9Kg4pZQtwF+CkcswTCCEWCCGyhBC5QogHLKz3E0K8b1q/RQiR5GyZPJFzxsQwscJkCPZFcQihKskLflRV2j2R/ZW6aEQOt/04LkRKyd5ywbfD7lTB2j3Lu93WPIPc1rvynOJaoqgi4th6mHil1f5w8xjZw2X1qpL+tDsh/TXVUqM79n2sRub6h8Jt3/B90wj8vA09xm8A5o5QcQ6HuKvyN/ecjZf9pcrA6m1ok7szYj5c9JzqcOBAfswr58PtBdw+N4Xh0SaXZlSqGjdQX27xM37eXrxw/VTmjYrmwY/2sOzH/pnkba29+BXg1P+2EMILWIIaRzsWuEYIMbbLZj8FKqSUI4B/ovpnabpwzuhYLvbaRHHoxL5nfUy8Sv3Id/ZQSd5UC3nf963fkJW0GR3Q6t0CxTVN1De3UT3qSuUO+vrRbkfXTowLpaaxVV3IbSC3qIYr/DYjZBtMtM5NBSfanxwy96w662FlsXz6S5X63BEpYcOz8MHNSsn89BuIHM6+wipGDxmEt1fPP/GEyEASIgLVVEB7SJileoyZO8ZaImc1JJ7e9xkg7oLBS7Wk9/Z12C5VQHwvQ0P9uefsESdWtPes6r52w8/bixevn8YZI6P53Ue7+SDd+crDWsWxBviLEOJZIcQNQojLOj4cJMsM1JyPg1LKZuA9YFGXbRYBb5heLwfOEcJZjWk8l4S2w4w1HOYL0cc+QADBMUoh7Hr/5IuVmUPfQVuz9T2jbOTz3ccY++iX7Y36HMlBk2smKTpU9bGqKYTvn7G4rXkGua31HDnFtSz22aAu6DHWF4olRqpgfXuzQ79g+MnTqkJ743MnNmxrhc9+Dd/8QXU4vnEFBEUipew0g6M35qRGsflgee/zXHoiYZZ67q6eozJfye/INNwBxJubD5N5vIZHLxpLoG+HCodIc5fcntuN+Pt48fIN05gzIorffribD7cVOFFa6xXHf4AY4P9QF+7lHR4fOEiWOKCjqiwwLbO4jZSyFagCIrvuSAhxhxAiXQiRXlJipwnuiexZjhEDzxdPoLqxm4u+NUy5XvnXc762vD77K9XkLuH0vh+jG7YdruDXy3bS1Gq0vxmfBcx388nRQcrNMmExbPy3xXnWqbHB+HkbbJ5Bbizax/DWA73WbnQl0Neb2EF+7Q0YATX0aczFahRu+UHVEeDdq2Db/2DOvXDZf9uL3woqGqhubO01vmFm7ogoapta2Xmk0iY5OxGRouaedBfnMA9tcqJ16qkU1zTyzOpszhgZzfnjBndeGZ6oLH8r2qv7+3jxyo1pnD48kvuX7+KTHUedJLH1WVWGHh6OT2S2Eynly1LKNCllWnS0HZ1aPRHTXPGaoadTZAzl+2w7Lrqp56qLgaUgecehTQ402QHyy+q5Y2k6Q0L9GRrqz7bDdvZTssCh0lr8vA0MGWSqNJ7/R+WC+OqhkwLlPl4Gxg4dZFNmVWV9M/Ma12IU3soasJGkyKCT26svfEq11fjkbnhtIRxYp3zt8//QKUvppBkcvXD68CgMAvsUtHmwU3cWR/ZXEDEcokZYXn8K8+SqTJpajfzRHBDviJePcjdb2V7d38eL/944nZnJkdy7bCcrdjpHebhTTtxROk8TjDcts7iNEMIbCAXsrF4aYBzdBhV5BKddQ1igT+cqclvx8oFJV6mgZm2X5onH9yj3joMzZKrqW7jl9a20GiWv3TydmcMj2ZFfYXdr866YmxsaDKYfamicmkCYtarzjAcTE+NC2Xu0CqOVMZec41Vc6rWBsqFnQlCUzfIlRwWR1zWmMmiIaq+RvxEq8uC6DyyOf91XWI1BwJjB1imO0EAfJsaHOSBAPku5pKq6/Gyb6+DQeu2mssCWg2V8tOMod5yR0n0iQ2Sq+r0V7VMDsHohwNeLV29OY3pSBK9vzHNKnNBqxSGEuEQIsV4IUWp6fC+EuNSBsvwIpAohkoUQvsDVnBhRa2YlYP6lXAGslY6+ong6ez4ALz+8xl7EWaNiWJdVbN8XZ/L1YGyF3e93Xp5jcj3YM7SpC82tRu58axv55fW8dMM0hkcHMzUhnNLaZvLLHTcVD+Cgpa64p/8Cxl8Ba/6oWpB3YEJ8GHXNbRy0cshSzf41xIpKDFbWbnQlKSqI8rrmzg0rAdJ+Cuc9AT9dDSPOsfjZ/YXVpEQHE+BrvTNgbmoUuwqqTj6eLZg70x7p4q46tF4VCDopFuaptLQZeXTFPuLCArj7rB4ssSGTlHvyhdPhicHw7AR481JY9VvY+oqqxq880imjLdDXm9duns7rt8zAy+D4MLBVfaaEEPcBfwGWAq+bFs8C3hFCPCKlfNpeQaSUrUKIe1AZXF7Aa1LKfUKIx4F0KeVK4FXgTSFELlCOUi4aM22tqmhv5HngH8rZo2P4eMdRduRXkJYU0fvnLREzWhU87XgLZnUoJsterYK+IbEOEV1KyUMf72HTwTKeuXISM1NU6GpaYjgA2/MrSIzsObXUWlrbjOSX1bOgqz9ZCFi0RN01f3SHats9dArQsYK88sRQph6IOvghVTKI8MkX90nGJNPfmldax6RhYSdWGAxw+j09fnZ/YZXN/+85I6L499pcNh0oY8H4wb1/wBKDJ6q2KvmbO7vnsr90WizMk1m66TBZRTW8dMO0npX8mb9VMa6yXPUozVExjyNbobnD4DbvgBOp8VGpBEWmqt9vgIM6VnfA2gaF9wP3SClf6bDsNSHEVuBxwG7FASClXAWs6rLs0Q6vGwEb+mecYuR9r4LZphYjZ46KxtsgWJNZ3HfFASpI/tmv1ByC+GmqB1bBj3Dm7xwjN7BkXS7LtxXwy3NSuWxqfPvykbEhBPt5s+1wBZdOie9hD9ZTUNFAq1Fadg34+MPVb8Mr58C718Dta2HQUIZHBxPg48WuI1W9y9FUw6iK71gbcA4LffvWrdUsW15ZF8XRCxV1zRRWNVodGDczJSGcQF8vNuSW9F1xeHmr4rj8Tby1+TA/5Jay5JopGLJXOyUW5skUVzfyz6+zmTcqmvPG9nLzZfCCoZPVoyNSQs1xpURKc1TKblkOHNuluvdKo2rtcsc6h8tvreIIBiwdfZ1pncYd2LMc/Aa1V3EP8vdhRnIEazKK+N0CO+YGjL8MvnwQ4463eHirL2c0rGEh0mHxjRU7j/L06mwunRLHr+andlrnZRBMHhbG9sOVDjkWnMio6m4OB8Exqingq+fBO1fBrV/i5RvE+LhB1vWs2r8SP9lE9uCfsLCPMppTcg/ZOH/c1sC4GV9vAzNTIu1vs54wC7n+KZ5e+SOVxgC2p39PWk2hjm904S+rMmhuNfLYRRYC4tYihIp7DRoCyV160LY2Q8Uh1QLeCVgb4/gEFVPoyuWcHIfQuIKWRnWXMbrzXPGzR8eQXVTLEXtiBP6hMPZiWna+z8dbc2jN/IJyEcbmxmG9f7YX0vPK+c3y3cxIiuDJyydY/BFNTQgj83g1tU32DTYyY45T9NROndixcMVrULRXua2MRibEhbGvsEp1Hu6B1h3vcMgYi29i36fR+ft4MTTU3+aiQ3PNi7U1HB2ZMyKKvLJ6u74rzXEzENLIGQGHiAzy5cjmT9QKW0f9DmA2Hyzjk52F3HlmisVZ9w7B21e1RDG5Wh2NtYojF3hACPGVEOIx0+NL4EEgSwhxr/nhFCk1vZP7tZqJ0aXFyPwxygy2K7sKOBB/CX5tdTyUmMkC//1sMkzl6le28uBHu/scUM0rreP2penEhQXw0g3T8PO27OedmhiOUcJue+oMOnCoVM3ICA88uWNsJ0aeB+f/FTI/gzWPMTE+lMYWI7kltd1/pjIf7/wNfNQ2l9RY+7oFJ0UF2W5xFFYzeJA/kcF+Nh9vbqrK/rKnivzfWaG0SgP3ji7j6hnDSCxbT3PsFGXFaWhpM/KHFfuIDw/g5/M8NzXZWsVxM1CBmvZ3k+kxyrTsFuAXpkfPUTuN89jzAQRFqwl+HUiKCiIlOog1mRZmkVtJfXMrd3znTyExXF/7Gj4t1cxfdAN3nJHC+z8eYf4z3/HFnmM2pcxW1jdz6+tq3Oj/bp5OeFD3/u8pw1SA3FH1HOZUXKtcBKf9TGUy/fAvTq/+AuhlBvnuZQB8bJxDaqx9XtykqCDyymxTHPsKq22Ob5gZERNM7CC/Prurfswr5z8bizgemEpS7R6unxDEZHGALT7T+7S/gcgbG/PIKqrhDxeNsynrzd2wtgAw2cpHirMF1ligsRqyvux2rvj8MbFsPljWZ1fPnz7L4GB5A62TrsVQVwIGH/xGzuehC8aw4u45xIT48fO3t3PHm9s4XtV7nnlTaxt3vLmNgooGXr4xrVdzPTTQh9SYYLbnO0hxlFhIxe0OIWDh3yDlLKK/+x1n+WV1P4NcStj1HodDJlPiNZj48O7nfFhDcmQQlfUtVNY3W7V9Y0sbB0pq+6w4hBDMGRHNDwdKbU7hrmtq5b5luxgWHkjsuHlwNJ0hx9ZiEJIXCkfQ2NLWJ5kGEoWVDTz7TQ5nj45h/hjPtsCsUhxCiNAe1mll4WoyP1d58t0MbDp7dAwtbZLvs20v8Ppq33He3ZrPz84YTsJZPwUEJM5qb1Q3IT6UFXfP5sGFo1mfXcK5z3zHm5sPd1soJ6XkwQ/3sPVQOX9fPJHpVmZ7TU0IZ3t+pdUFeN3R0NxGYVWj9YoDVCHk4tcREcN5zvAMJYf3W97u6HYoy2GNz9kMjw62O3/+pGaHvZB5vAajtD0w3pG5qVFU1rfY3B/siVUZHKmo5+nFk/BJPl3Nud/wDE0BsWysj2PVnmN9lmkgkFNUw+IXN2GUkj9cNLbvAXE3wVpX1W4hxEmjY4UQtwI7HSqRxnb2fABhCRBv2SWQlhhOaICPze6qoupGHvhwN+PjBnHvuSPVMX7yNJz1+07beXsZ+NmZw1n96zOYOCyURz7Zy5UvbSK3uOakfT63JpePdhzlvnNHsmhy11Zk3TMtMZyqhharC/C6w+z6sUlxAASEwbXv4+Vl4Lflj9JcY6HN9a53wduf9+qm2u2mUjKamh1a6a4yX+zHDe32Pq9XZo9QcQ5b2o+syyrmnS353DE3hRnJEScaHlbk4Tv6fFKiglm6qX8HDbkTGw+UctkLG2luM/L+HbMcVo/kSqxVHO8A3wgh/iKE8BJChAshPgSeBX7lLOE0VlBbAge/VRXP3dzFeHsZ1CzyTOuryI1Gyf0f7KKhpY1/XT0FX2/TV2X6bZBwmsXPJEYG8dZPT+PvV0wkp7iWC/61gWe/yaapVbkpPt5RwD+/yebyqfGdW0dbwdTEMAC22xnnaG9u2JdslohkdsxaQhwlNL97Xeeuwa3NsHc5rakLya4ykGpFkWBvDIsIxCBQ0wCtYH9hNSH+3sSHB/S+cTdEh/gxZsggvrey/UhlfTO/W76bkbHB/PrckWphSKxqegiIUQu4fmYiO49Udu/iG8B8uK2Am17bypBQfz6+63QmxPddqbsT1sY4HkSNjb0e2ArsRvWSmiqlfM154ml6Zf8nVs0VP3t0DGV1zeyyssPraz8c4vucUh65cOyJoTJWIIRgcdow1tx3JgvGD+bZb3K48LkNLN2Ux++W72FmSgR/vcxy2m1PpEQFExrgY3ecwy7FAcRPPpsHW24juHAjrLr/REPEnNXQUMGRBFUpPiLG/vnrft5eDA0LOLnZYTfsM7VSt9cNMjc1im2HK6hv7j0m9uiKfZTXNfPMlZPx9+kQ7E08Hbz9IflMLp8WT4CPF0tdMBvbVUgp+dc3Odz3wS6mJ0XwwZ2n2x3zcidsaXK4AfgCmALEAo9LKa1r2ahxHvs+Ns0V7zrzqjPzRsbgZRBWpeVmHKvmqS+zmD8mlmtnJPRJrKhgP567Zgr/u3k69c1tPLpiH/ERAbx4/bQT1osNGAyCKQlhdmdWHSypI3aQH0F+1ta+diYhIpBvfM9mXcwNsO112Py8WrHrXQiKZof3VACHuKrA3Oywd8XRZpRkHq+2K75hZs6IKFraJFsOWZ46Z+az3YWs3FXI/52Tyvi4LnfSZz8KN30GfkrhXzIljpW7Cqmosy7Q78k0txr5zfLd7db167fMIDSgl9RvD8Pa4PhIYAtwLjAP+BPwkRDin6aGhBpXUFsMhzfC2N77IYUG+pCWGM6ajJ7jHI0tbfzyvR2EBvrwt24K8mzhrNExrP71GTx64Vje/OlphAX2/esyLSGcnOJauxrxHSqt7bO1AcqimhgfxjOti9V8jK8ehp3vqLbhE64ku7QRXy8DiRGOubtMilS1HL2lOh8qraWxxWhXfMPMjOQIfL0NPablFlc38vtP9jJpWBh3zbMwNjgkFoadiLndOCuRplYjy508YMjVVDWo7s7LtxXwq/mpPL14Yp9ulNwda/+iHUAGMFlKuV5K+SfgDOAnQLqzhNP0QubngFQXMCuYPyaWzOM1FFR07zN/8otMsotqeXrxpD4VkVkiyM+bW+ckExfWd987qEJAgB12uKtUDYd91sCE+FAyi+povOh51T/ok5+DsQUmXU1ucQ0p0UG9jmy1lqSoIGoaWynv5U59X6FqNdLXVNyO+Pt4MT0pvFvFIaXkgY/20NDcxj8WT7Lqbx0zZBDTk8J5a0v3GXeeztHKBha/uJEtB8t5evEkfjV/pMdnT3WHtd/un0kpr5dSVpsXSCm3AFNRMQ+NK8hYqYKQseOs2vxsU+742m6yq9ZlFvP6xjxunZ3MmSPdbwDWpGFhGARsz6/s0+cr6pqpqG8hxc42DxPjQmlpk2SVtcE176l54EMmweAJ5BTXWtU911qszazaX1iNr5fBYceeMyKarKIaiqtPrstZln6EtZnF/G7BaJuOd8OsJA6X1fOdvXM/3JC9R6u4ZMkPHKtqZOmtM7himmMacror1gbH3+pmea2U8jbHiqSxioYKNedgzEXdZlN1ZXh0MMlRQRbdVaW1Tfxm+S5GDw7htwtGOVpahxDs582owYP6nFl1qK+puF0wZ8bsPloFIYPhrk1wwyc0thrJL68n1QGBcTPm1M3eMqv2H6tm5OBgfBxk6XTXfuRIeT2Pf7qfWSmR3Hx6kk37XDBuMFHBfrzphNRcV47lWZNRxJUvbcLXy8CHPz+d00fYPrjL0+jxWyaEeEcIEdLh/Z1d3ocLIdY7U0BNN2R9oQYsjVlk08fOHh3DpgNl1HWoIpdS8tvlu6lubOVfV0/pnB3jZkxLDGPnkco+DafK6zhn3A7iwgKIDPI9MYPcPxQCI8gtrkVKxwXGAYaFq5TcnjKrpJTtGVWOYuyQQUQE+Xaq5zCnaAsh+PviiSemJ1qJr7eBa2YMY11WsX1NN7tQ1dDCBc9t4K9fZDhsn9by5ubD3L40nZToID6+63RG2tmfzFPo7fbkKqCjY/opoKMPwxeY7WihNFawfyUMioe4qTZ97JwxMTS3GTvdSb61JZ+1mcU8uHA0owa79xd/akI4tU2tZBedXFzYG4dK6/AyCIbZmRYphGBCfOhJPatyi1XzQ0fUcJjx9TYQHx7Ybi1Z4nh1I+V1zQ4JjJsxGASnD49kQ25p+938az8cYsuhch69aGyfU0uvPS0BgxC8tdkxVoe66dlFxrFqXll/kJw+fC/6gtEo+cuqDB75ZC9njYrh/TtmETOob7NXPJHeFEfXW4qBGenxNJpq1LhIG9xUZqYnRRDi792elptbXMOfP9vPmSOjbXY9uIKOEwFt5WBpHcPCAxyS5TIxLpSc4loamk/0YMoprsHbIBxeGZwUFdSjxbG/sG8zOHpjbmoUJTVNZBXVkFNUw1NfqRTtxXb474eEBnDumFjeTz/ikP5Vr/2Qx1f7irjnrBEE+Xnz1y8y7d5nbzS3GvnFuzt4ef1BbpiZyEs3TOtzerenMvDyxE4Fclar3lRWpOF2xcfLwJkjo1mbWUJjSxv/9+5Ogvy8+fviiR6RAZIQEUhkkG+f6jlsam7YCxPiw2gzSvYfO2F15BTVkhQV5PD0y+TIQA6X1Xfrx99XWI0QKnPJkcxJVc6Fb7NKuHfZLoL9vPtUvNmVG2clUlnfwqe7Cu3az/b8Cv66KoNzx8Zy33kjueesEazNLGajHW3hreGV7w/y+Z5jPHTBaB5fNM5hGXSehDV/8cDMnfNk9q9ULdSHWW790Rvzx8RSWtvE7UvT2X+smqcun0hMiGeY2UIIpiaGs8PGzCoppUNScc2YZ5B3dFflFtc61E1lJikqiNqmVkprLafk7i+sJikyiGAH3/XGhQWQEh3EP7/OZs/RKp64ZDzRIfanaM8aHsmImGDetMNdVVHXzC/e2cGQMH+evmISQghuOj2JuLAAnliV4bSU38NldTy3JocLJgzmjjOGe8TNljOwRnH8VQjxnBDiOVRM4w8d3j/hXPE0J9HSADlfq0l/hr4Fsc8cGY1BqEZ2189MYH5vM4/djKkJ4RwqraOstsnqzxRVN9HQ0mZ3YNxM7CB/YkL82vsvNbW2kVdW5zTFAd2n5O47VuXQwHhH5o6IoqnVyKVT4lg4YYhD9imE4IaZiewuqGJnH4ZzGY2Se5ftpKSmiSXXTiXUNJDL38eL3y4Yxb7Caj7ZedQhsnZESsmjK/bhbRA8eqF1KfADld4Ux3pgODDB9NgIJHR4P9y0jV0IISKEEF8LIXJMz+HdbPelEKJSCPGZvcf0WA6shZa6PrmpzIQH+TJ7RBSpMcE8fEHPrUrckWnthYCVVn/mYKkKXNtbw9GRifGhKiUXFXg3ShjhhKya5Mju26tXNbRwpLzB4fENM4vThnH+uFgeu8ixF8rLpsYR5OvVp9Tcl9YfZF1WCb+/cAwT48M6rbto4lAmxofy9FdZDp8BsmrPcb7LLuG+80YxONQzLHRn0aPikFLOk1Ke1dvDAXI8AKyRUqYCa0zvLfF34AYHHM9z2b8S/MMgaa5du3nphml8cvdsj5xCNjE+FG+DYJsNAXJ7mxtaYkJcGAdKaqltaiWnyPEZVWbiwwPwNgiLAfKMY84JjJsZHxfKSzektd/VO4oQfx8unRrHp7sLe62K78iWg2U8vTqLn0wcwg0zE09abzAIHrpgDIVVjbz2wyGHyVvT2MIfP93HuKGDuHHWycc91XCXqM4i4A3T6zeASyxtJKVcA/RPvp070tqs6jdG/0QNF7KDQF9vj80E8ffxYtxQ2woBD5XU4e9jYLADUyYnxociJew7WkVOcS0G4VjFZMbby8CwiECLrqr9Dmw10t/cOCuJ5lYjy9KPWLV9aW0Tv3h3BwkRgTzZQ5B+Zkok88fE8vy6Aza5M3viH6uzKalt4olLJ5ySwfCuuMsZiJVSmkeEHUd13+0zQog7hBDpQoj0kpIB1N7g0HpoqlJpuKc4UxLC2VVQSUub0artD5XWkRQZZHPRWk+YO8LuOVpFbnENiZFBTiueTIoMtFg9vq+wmqhgP49JbujIyNgQTkuO4K3Nh3st6GwzSn713k6qGlpYcu1UQvx7vnF6YOFoNUtmTY7dcu4pqGLppjxumJnI5GFhdu9vINBvikMI8Y0QYq+FR6fSZ6lyDu1KiZBSviylTJNSpkVHu1/PpT6TsRJ8gyHFEd5Bz2ZaYjiNLUYyj1lngB4qrSPFQYFxM9EhfgwN9Wd3QRU5RY7tUdWVpKggDped3CV3X2GVR1obZm6clURBRQPfZvXctfnfa3PYkFvK44vGWeWWGxETzDUzhvHOlnwOlNT2Wb42o+ThT/YQGezH/ee7ZyseV9BvikNKOV9KOd7CYwVQJIQYAmB6tm3G6amAsU11wx15Pvh43t2lozF3yt12uOeZEQAtbaqHlDPcSBPiQ9meX8GhUudkVJlJjgqivrmN4poTrpem1jZyi2s9WnGcNy6WmBC/HkfLbsgp5V9rcrhsahxXpg2zet+/mj8Sfx8v/mZHUeDbWw6zu6CKRy4cy6BerJxTCXdxVa0EbjK9vglY4UJZ3JPDG6G+1OoW6gOdoaH+DB7kb1Wn3IKKBlqN0mE1HB2ZGB/Wvn9H9qjqSpKFzKqcolpajdJpgfH+wMfLwDUzEvguu8Ri8L+oupFfvb+DEdHB/PmS8TbVTUQF+/HzecNZvb+ILQfLbJatuLqRv3+ZxdzUKC6a6JhU5IGCuyiOJ4FzhRA5wHzTe4QQaUKI/5o3EkJ8D3wAnCOEKBBCnO8SaV1Bxko1inPEfFdL4haoQkDrJgIeMqXiOsXi6DD5zpFdcbtilr3jxfVEYNyz51hfe1oC3oaT+1e1tqnWHnVNbbxw/VQCfW1P5rh1djKDB/nzlz4UBf7p8wya2ow8vsg2hXUqYJfiMMUtDtgrhJSyTEp5jpQy1eTSKjctT+/Ytl1KOVdKGS2lDJBSxkspv7L32B6B0QgZnyql4ee8u1pPY2pCOEcrGyiyMDOiIwdL1MXWkTUcZsyKQwhsms1uK0PDAvD1MnRqdrivsIogXy+HTRt0FbGD/Dl/3GCWpR/p1Pvrma+z2XqonL9cNr7PM9wDfL24//xR7Cqo4rM9x3r/gIn12SV8uquQu+eNcMoNh6djr8XxIw4oANT0wtFtUHNMu6m6YI5z9JaWe6i0jrBAH8KDHD/lODzIl2ERAQwLD3RqTYyXQTAsIqCzxXGsmjFDBjk0U8xV3DArkerG1vb+Vesyi3n+2wNcMyOBS6fYNxTp0ilxjB0yiL99kWlVUWBjSxuPrNhLSlQQd85LsevYAxW7FIeU8kEp5S2OEkbTDRkrwOCjAuOadsYNHYSvt6HXTrmqR5Xz7hpvnZ1ssRjN0SRHBZFnSsk1GiX7C6s9Or7RkdOSIxgZG8zSzXkcrWzg18t2MnbIIP5wkf2dDbxMRYFHKxtYuimv1+2fX5fL4bJ6/nTJePy8Pa9Atj9wlxiHpjukVNXiKfMgIMzV0rgVft5eTIgL7TXO4WzFccvsZG4/w/l3pomRQeSV1WE0Sg6X11PX3ObRGVUdEUJww6wk9h6t5pqXN9PaJnn+uqkOq4uZkxrFvFHR/GdtLhU9VKrnFtfywncHuGTyUGafApP8+opVikMI8Vo3j1eFEEuEEL8WQgx1trCnJMd3Q+VhXfTXDdMSw9l7tJqmVssuiPrmVo5VNTolvtHfJEUF0dRq5Hh144AJjHfk0ilxBPt5k19ez1NXTGxv7ugoHlw4htqmVv69Ntfieiklj3yyF38fLx7+ief1cOtPrLU4ooHLUK1ARpgel5iWjQJ+C2QJISY7XMJTnYxPQRhUmxHNSUxNCKO5zcjeo9UW15tdO85Ixe1vzM0O88rq2FdYhbdBODUFuL8J9vPm8UXj+OPF47jAQZ14OzJqcAhXpg3jzc15HLbQvuWTnUfZdLCM3y0Y7ZD28QMZaxXHD8AXQLyU8gwp5RlAPLAKWA0kAp8D/3CKlKcy+1dC4mwI0mazJaYmmDvlWnZXOaO5oatIilLZU3ml9ew/Vs2ImOAB54O/bGo8NzlxEuW9547E22DgqS+zOi2vqm/hz59lMHlYGNfOSHDa8QcK1iqOXwKPSynbm+WYXj8B/FpK2Qz8DZjscAlPZUqyoDQLxi7qfdtTlJhB/sSHB3Qb5zDXcJgvup7M0FA19lZZHAMnMN6fxAzy52dnpvD5nmOdvjN/+yqTivpmnrh0/IDIUnM21iqOYMCS7TjYtA6gGvDMdqvuyv6V6nn0ha6Vw82ZlhjO9vwKi6NVD5bWMSTUv0/FY+6GwSBIjAjkx7xySmqaBlR8oz+544wUYkL8eOLz/Ugp2Xa4gne25HPL7GR9Tq3EWsXxMfCqEGKxECLJ9FgMvAp8ZNpmBpDtDCFPWTJWQvwMGKTbHfTE1IRwiqqbOFrZcNI6Z2dU9TdJUUHtA6ycNfVvoBPo6829545ke34ln+0+xsMf72HwIH9+fe5IV4vmMVirOO4EvgLeAg6YHm8BXwJ3mbbJAG53tICnLOWHVEaVHZP+ThXMEwEt9a0aaIqj49+iXVV9Z3HaMEbFhnDfsl1kHq/hsYvHOnxm+0DGKsUhpayXUt4JRABTTI8IKeXPpZR1pm12Sil3Ok3SU42MT9WzTsPtldGDQwjw8TqpgryirpnK+pYBpTjMzQ6HRQQQGqC7tfYVL4PgwQtG09xm5OzRMZw/brCrRfIorFKxQohfAe9IKYuB3U6VSKPIWAlDJkF4kqslcXu8vQxMGhZ6UgX5QVNGlaPncLgSc5Bfu6ns58yR0bx2cxpTE8J1E0MbsdZVdS9QIIT4UghxnRDC81NU3Jmqo1Dwo7Y2bGBqQjj7C6s7Nck7kYo7cGodzI0Ux+sgrt0IITh7dCxhgY7vYTbQsVZxJALnA0eAf6MGL70lhFgghNBtSxxN5ufqeYxOw7WWaYnhtBoluwsq25cdKq3F2yCIDw9wnWAOJnaQPy/dMI0bZyW5WhTNKYy1MQ4ppVwnpbwdlYJ7E+CPyqgqcKJ8pyYZKyF6NETrLA9rmWIqBNzWwV11qLSOhIhAfLwG1r3N+eMGExqo4xsa12HzL8pU7LfJ9DiMUiQaR1FXCod/0C3UbSQiyJeUqCC2H65sX3awZGBlVGk07oLVikMIESKEuEUI8Q2QD9wGvAMMd5ZwpySZn4E06jTcPjAl4UQhoNEoySvTikOjcQbWZlUtBy5AVYe/DzwopfzRmYKdsmR8qjKpYse7WhKPY1piOB9uL+BwWT2+3gYaW4wkD6CMKo3GXbC24qUJuBxYLaXs1L9aCDFfSvmNwyU7FWmohIPfwcyfq1mkGpuYmhgGwLbDFQwO9QcGRnNDjcbdsEpxSCmv6/heCBEH3ALcisq4GlgtOl1F9pdgbNFNDftIakwIIX7ebM+vYIypziFlAKXiajTugi0xDi8hxGVCiFVAHnAp8CJqNofGEexfCYPiYOhUV0vikXgZBJMTwth2uIJDpXUE+HgRO0jPVdBoHE2vikMIMUoI8XegEHga2G5adYOU8ikp5SF7hRBCRAghvhZC5Jiewy1sM1kIsUkIsU8IsVsIcZW9x3UrmmrhwBpV9GcYWOmj/cnUhHCyi2rYU1BFclSQrgjWaJxAj1coIcT3wGYgHLhSSpkipfy9E+R4AFgjpUwF1pjed6UeuFFKOQ5YADwrhAhzgiyuIfdraG3U1eJ2MjUxHKOErXnlOjCu0TiJ3m5tZwFLgX9KKb9zohyLgDdMr99AjaXthJQyW0qZY3pdCBSjRtoODPavhKBoSJjlakk8msnDwtrzCgbCnHGNxh3pTXFMRwXQNwghdgghfi2EcEbBX6yU8pjp9XEgtqeNhRAzAF9Ue3dL6+8QQqQLIdJLSkocK6kzaGmEnNVqrrhB5xnYQ2iAD6kxKiCuM6o0GufQo+KQUu6QUt6Nmv73DHAxql+VAfiJpVhEdwghvhFC7LXw6JRCJNUYt5NHuZ3YzxDgTeAWKaWxG7lfllKmSSnToqM9wCg5sBaaa3W1uIMwz+fQikOjcQ7WpuM2oi7WbwohRqCqxn8N/FkIsVZKudCKfczvbp0QokgIMURKecykGIq72W4Q8DnwsJRyszWyewQZn4J/KCTNdbUkA4Lzxg7m26wSUmNDXC2KRjMg6Uuvqlwp5QPAMOBKoNkBcqxENU7E9Lyi6wZCCF/UCNulUsrlDjime9DWAlmrYNQF4K3bOzuCs0bHsOnBc/REN43GSfQ571NK2SalXCGldES12pPAuUKIHGC+6T1CiDQhxH9N21wJnAHcLITYaXpMdsCxXcuh9dBYqd1UGo3GY3CLWzIpZRlwjoXl6Si3GFLKt1BzzgcWGSvBNxiGn+1qSTQajcYqdKWZKzG2qaFNqeeBj7+rpdFoNBqr0IrDleRvhroSXfSn0Wg8Cq04XEnGSvD2VxaHRqPReAhacbgKo1Gl4Q4/B/x0B1eNRuM5aMXhKgq3Q/VRPelPo9F4HFpxuIqMlWDwhpELXC2JRqPR2IRWHK5AStXUMPlMCAhztTQajUZjE1pxuIKivVBxSLupNBqNR6IVhyvYvxKEAUZf6GpJNBqNxma04nAFGSshcTYERblaEo1Go7EZrTj6m5JsKMnURX8ajcZj0Yqjv8lYqZ614tBoNB6KWzQ5PKXIWAnx02HQUFdLotEMKFpaWigoKKCxsdHVongU/v7+xMfH4+PjY/VntOLoTyry4NguOPdPrpZEoxlwFBQUEBISQlJSEsI8eF7TI1JKysrKKCgoIDk52erPaVdVf5LxqXrWbiqNxuE0NjYSGRmplYYNCCGIjIy02UrTiqM/yfgUBk+ACOs1u0ajsR6tNGynL+dMK47+ovoYHNkCYxwxMFGj0Whch1Yc/UXmZ+pZV4trNJpuePHFF1m6dCkAr7/+OoWFhe3rbrvtNvbv3+8q0Tqhg+P9xf4VEDUKoke5WhKNRuOm3Hnnne2vX3/9dcaPH8/QoSoD87///a+rxDoJrTj6g7oyOPwDzL3P1ZJoNKcEf/x0H/sLqx26z7FDB/GHi8Z1uz4vL48FCxYwbdo0tm/fzrhx41i6dCmbNm3i/vvvp7W1lenTp/PCCy/g5+fHAw88wMqVK/H29ua8887j6aef5rHHHiM4OJikpCTS09O57rrrCAgIYNOmTSxcuJCnn36a9PR0Dhw4wN///ndAKZj09HT+85//8NZbb/Hcc8/R3NzMaaedxvPPP4+Xl5dDzwO4iatKCBEhhPhaCJFjeg63sE2iEGK7EGKnEGKfEOJOS/tyS7I+B2nU2VQazQAnKyuLu+66i4yMDAYNGsQzzzzDzTffzPvvv8+ePXtobW3lhRdeoKysjI8//ph9+/axe/dufv/733fazxVXXEFaWhpvv/02O3fuJCAgoH3d5Zdfzscff9z+/v333+fqq68mIyOD999/nx9++IGdO3fi5eXF22+/7ZS/010sjgeANVLKJ4UQD5je/67LNseAWVLKJiFEMLBXCLFSSlnYdWdux/6VEJYIgye6WhKN5pSgJ8vAmQwbNozZs2cDcP311/OnP/2J5ORkRo4cCcBNN93EkiVLuOeee/D39+enP/0pF154IRdeaH3D0+joaFJSUti8eTOpqalkZmYye/ZslixZwrZt25g+fToADQ0NxMTEOP6PxH0UxyJgnun1G8C3dFEcUsrmDm/9cBNrqVcaKuHgtzDzTtCpghrNgKZramtYWBhlZWUnbeft7c3WrVtZs2YNy5cv5z//+Q9r1661+jhXX301y5YtY/To0Vx66aUIIZBSctNNN/HXv/7V7r+jN9zl4hsrpTxmen0ciLW0kRBimBBiN3AE+Ft31oYQ4g4hRLoQIr2kpMQ5EltL9ldgbNFpuBrNKUB+fj6bNm0C4J133iEtLY28vDxyc3MBePPNNznzzDOpra2lqqqKCy64gH/+85/s2rXrpH2FhIRQU1Nj8TiXXnopK1as4N133+Xqq68G4JxzzmH58uUUFxcDUF5ezuHDh53xZ/afxSGE+AYYbGHVwx3fSCmlEEJa2oeU8ggwUQgxFPhECLFcSllkYbuXgZcB0tLSLO6r38hYCSFDIG6aS8XQaDTOZ9SoUSxZsoRbb72VsWPH8txzzzFz5kwWL17cHhy/8847KS8vZ9GiRTQ2NiKl5JlnnjlpXzfffDN33nlne3C8I+Hh4YwZM4b9+/czY8YMAMaOHcuf//xnzjvvPIxGIz4+PixZsoTExESH/51CStdeVwGEEFnAPCnlMSHEEOBbKWWPeatCiNeAVVLK5T1tl5aWJtPT0x0orQ0018FTw2HqDXDB310jg0ZzipCRkcGYMWNcdvy8vDwuvPBC9u7d6zIZ+oqlcyeE2CalTLO0vbu4qlYCN5le3wSs6LqBECJeCBFgeh0OzAGy+k3CvpDzNbQ2wBhd9KfRaAYO7qI4ngTOFULkAPNN7xFCpAkhzFUvY4AtQohdwHfA01LKPS6R1loyVkJgFCSe7mpJNBqNk0lKSvJIa6MvuEVWlZSyDDjHwvJ04DbT668Bz8lnbWlUgfHxl4PB8QU4Go1G4yrcxeIYeBz8FpprtZtKo9EMOLTicBYZK8EvFJLPcLUkGo1G41C04nAGbS2Q+TmMWgjevq6WRqPRaByKVhzOIO97aKzULdQ1Go3DqKys5Pnnn29/X1hYyBVXXOESWbTicAb7V4JPEAw/29WSaDSaAUJXxTF06FCWL++xjM1puEVW1YDC2KbcVKnngk9A79trNBrH88UDcNzB2fqDJ8DCJ7tdnZeXx8KFC5kzZw4bN24kLi6OFStWUFhYyN13301JSQmBgYG88sorjB49mgMHDnDddddRV1fHokWLePbZZ6mtraW2tpZFixZRUVFBS0sLf/7zn1m0aBEPPPAABw4cYPLkyZx77rncfffd7QWHM2fO5NVXX2XcONXccd68eTz99NOMGTOGX/ziF+zdu5eWlhYee+wxFi2yv/2RtjgcgdEIBdtgzePwwmyoK4axujeVRnOqkZOTw913382+ffsICwvjww8/5I477uDf//4327Zt4+mnn+auu+4C4Je//CW//OUv2bNnD/Hx8e378Pf35+OPP2b79u2sW7eO++67DyklTz75JMOHD2fnzp3tszjMXHXVVSxbtgyAY8eOcezYMdLS0njiiSc4++yz2bp1K+vWreM3v/kNdXV1dv+d2uLoK61NcGi9si6yvoDa4yC8VLHf9Kdh7CWullCjOXXpwTJwJsnJyUyePBmAadOmkZeXx8aNG1m8eHH7Nk1NTQBs2rSJTz75BIBrr72W+++/HwApJQ899BDr16/HYDBw9OhRiopOasnXiSuvvJLzzjuPP/7xjyxbtqw99rF69WpWrlzJ008/DUBjYyP5+fl2t2bRisMW6stVG5GszyF3jarT8AmCEefA6J9A6nkQGOFqKTUajYvw8/Nrf+3l5UVRURFhYWHs3LnT6n28/fbblJSUsG3bNnx8fEhKSqKxsbHHz8TFxREZGcnu3bt5//33efHFFwGlhD788ENGjXLsyGrtquqNijzY9Dy8fiH8fQR8fAfkb4YJV8C1H8BvD8JVb8Kkq7XS0Gg0nRg0aBDJycl88MEHgLqQm1uoz5w5kw8//BCA9957r/0zVVVVxMTE4OPjw7p169pbo/fUZh2Uu+qpp56iqqqKiRNVk43zzz+ff//735ib2e7YscMhf5dWHN1ReQSePx3+NQm+ehDqSmHOr+C2tXBvJlz0Lxh5Hvj4u1pSjUbjxrz99tu8+uqrTJo0iXHjxrFiherh+uyzz/LMM88wceJEcnNzCQ0NBeC6664jPT2dCRMmsHTpUkaPHg1AZGQks2fPZvz48fzmN7856ThXXHEF7733HldeeWX7skceeYSWlhYmTpzIuHHjeOSRRxzyN7lFW3Vn0ue26m2t8N61qvJ79AUQkeJ44TQajcNwdVt1W6mvrycgIAAhBO+99x7vvvtuu1Lpb2xtq65jHN3h5Q3XLXO1FBqNZoCybds27rnnHqSUhIWF8dprr7laJKvRikOj0WhcwNy5cy2OjPUEdIxDo9EMGAa6690Z9OWcacWh0WgGBP7+/pSVlWnlYQNSSsrKyvD3ty3JR7uqNBrNgCA+Pp6CggJKSkpcLYpH4e/v36ly3Rq04tBoNAMCHx8fkpOTXS3GKYF2VWk0Go3GJrTi0Gg0Go1NaMWh0Wg0GpsY8JXjQogS4LALDh0FlLrguO6MPicno8/JyehzcjKuOCeJUspoSysGvOJwFUKI9O7K9U9V9Dk5GX1OTkafk5Nxt3OiXVUajUajsQmtODQajUZjE1pxOI+XXS2AG6LPycnoc3Iy+pycjFudEx3j0Gg0Go1NaItDo9FoNDahFYdGo9FobEIrDgcghMgTQuwRQuwUQqSblkUIIb4WQuSYnsNdLaczEUK8JoQoFkLs7bDM4jkQiueEELlCiN1CiKmuk9x5dHNOHhNCHDV9V3YKIS7osO5B0znJEkKc7xqpnYsQYpgQYp0QYr8QYp8Q4pem5afsd6WHc+K+3xUppX7Y+QDygKguy54CHjC9fgD4m6vldPI5OAOYCuzt7RwAFwBfAAKYCWxxtfz9eE4eA+63sO1YYBfgByQDBwAvV/8NTjgnQ4CpptchQLbpbz9lvys9nBO3/a5oi8N5LALeML1+A7jEdaI4HynleqC8y+LuzsEiYKlUbAbChBBD+kXQfqSbc9Idi4D3pJRNUspDQC4ww2nCuQgp5TEp5XbT6xogA4jjFP6u9HBOusPl3xWtOByDBFYLIbYJIe4wLYuVUh4zvT4OxLpGNJfS3TmIA4502K6Ann8oA417TG6X1zq4ME+5cyKESAKmAFvQ3xXgpHMCbvpd0YrDMcyRUk4FFgJ3CyHO6LhSKvvylM571uegnReA4cBk4BjwD5dK4yKEEMHAh8CvpJTVHdedqt8VC+fEbb8rWnE4ACnlUdNzMfAxymwsMpvUpudi10noMro7B0eBYR22izctG/BIKYuklG1SSiPwCidcDKfMORFC+KAukG9LKT8yLT6lvyuWzok7f1e04rATIUSQECLE/Bo4D9gLrARuMm12E7DCNRK6lO7OwUrgRlPGzEygqoObYkDTxT9/Keq7AuqcXC2E8BNCJAOpwNb+ls/ZCCEE8CqQIaV8psOqU/a70t05cevviqszCjz9AaSgMhx2AfuAh03LI4E1QA7wDRDhalmdfB7eRZnTLSif60+7OweoDJklqGyQPUCaq+Xvx3Pypulv3o26AAzpsP3DpnOSBSx0tfxOOidzUG6o3cBO0+OCU/m70sM5cdvvim45otFoNBqb0K4qjUaj0diEVhwajUajsQmtODQajUZjE1pxaDQajcYmtOLQaDQajU1oxaHROBEhxM1CiFpXy6HROBKdjqvR9BEhRG8/njeAnwMhUnUV0GgGBN6uFkCj8WA6VvZeiGoL0XFZg5SyAWjoV6k0GiejXVUaTR+RUh43P4DKrsuklFVdXVWm4Tx7hRA3mQaA1Qkh/ieE8BVC3CWEOCKEKBNCPCOEMHT4nK8Q4m9CiAIhRL0Q4seBOuxJ4/5oi0Oj6X+SUDMVLkS1w/4QZakcQ/U6Gw0sA34wrQP4H6pT6rWo9iUXAJ8KIaZLKXf1p/AajVYcGk3/4wXcIqWsAvYKIb4EzgTipJTNQIYQ4gfgLOBDIcRw4BogSUqZb9rHf4QQ84GfAXf1/5+gOZXRikOj6X/yTUrDTBGQbVIaHZfFmF5PRTX7268aqbbjB6x1pqAajSW04tBo+p+WLu9lN8u8TK8NpvfTLWynA++afkcrDo3G/dmBsjgGSynXuVoYjUYrDo3GzZFSZgsh3gZeF0LcB2wHIoB5wEF5YoqeRtMvaMWh0XgGt6CG9zyFGhVajpr6pi0QTb+jK8c1Go1GYxO6AFCj0Wg0NqEVh0aj0WhsQisOjUaj0diEVhwajUajsQmtODQajUZjE1pxaDQajcYmtOLQaDQajU1oxaHRaDQam/h/RPD+dsNeeuoAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plt.plot(header,(values[values[:,0]>0]).mean(axis=0),label=\"positive\")\n",
"plt.plot(header,(values[values[:,0]<0]).mean(axis=0),label=\"negative\");\n",
"plt.xlabel(\"Time\",size=14)\n",
"plt.ylabel(\"Avg. Expression\",size=14)\n",
"plt.legend()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": ""
},
"tags": []
},
"outputs": [],
"source": []
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.9.6"
}
},
"nbformat": 4,
"nbformat_minor": 4
}

