Dimensionality Reduction¶

11/2/2023¶

print view

notebook

In [2]:
%%html
<script src="https://bits.csb.pitt.edu/preamble.js"></script>

Recall¶

In [42]:
from matplotlib.pylab import cm
import numpy as np
import scipy.cluster.hierarchy as hclust
import matplotlib.pyplot as plt
data = np.genfromtxt('Spellman.csv',skip_header=1,delimiter=',')[:,1:]
Z = hclust.linkage(data,method='complete')
leaves = hclust.leaves_list(Z)
ordered = data[leaves]
print(data.shape)
plt.matshow(ordered,aspect=0.01,cmap=cm.seismic);

(4381, 23)
In [9]:
%%html
<div id="howdim1" style="width: 500px"></div>
<script>
    var divid = '#howdim1';
	jQuery(divid).asker({
	    id: divid,
	    question: "What is the dimensionality of this data?",
		answers: ['1','2','23','4381','None of the above'],
        server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
		charter: chartmaker})
    
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();


</script>

Dimenionality Reduction¶

$$f(\mathbb{R}^N) \rightarrow \mathbb{R}^M, M < N$$

Usually used for visualization so reduce to 2 or 3 dimensions.

Goal is for distances in $\mathbb{R}^M$ to be representative of distances in $\mathbb{R}^N$

PCA¶

Recall: principal component analysis finds an orthogonal basis that best represents the variance in the data.

In [10]:
from sklearn.decomposition import PCA
In [11]:
model = PCA(n_components=2) #specify number of components
pcaresult = model.fit_transform(data)
In [12]:
model.explained_variance_ratio_
Out[12]:
array([0.29005293, 0.15421722])
In [13]:
pcaresult
Out[13]:
array([[ 0.53743596,  0.04236283],
       [-0.52117275,  0.23262807],
       [-0.92718811, -0.02687601],
       ...,
       [ 2.22481438, -0.63181596],
       [-1.90513202,  0.62147871],
       [-1.52881942,  1.02728409]])
In [14]:
plt.scatter(pcaresult[:,0],pcaresult[:,1],s=4,alpha=.1)
plt.xlabel('PCA1'); plt.ylabel('PCA2');
In [39]:
import seaborn as sns
plt.figure(figsize=(16,2))
sns.heatmap(model.components_,cmap=cm.seismic,yticklabels=['PC1','PC2'],
            square=True, cbar_kws={"orientation": "horizontal"});

PCA 3D¶

In [43]:
model = PCA(n_components=3) #specify number of components
pcaresult = model.fit_transform(data)
fig = plt.figure(figsize=(10,10))
ax = plt.axes(projection='3d')
ax.scatter3D(pcaresult[:,0], pcaresult[:,1], pcaresult[:,2])
ax.set_xlabel('PCA1');
ax.set_ylabel('PCA2');
ax.set_zlabel('PCA3',rotation = 90);
plt.show()

PCA and eigenvalues¶

In [47]:
model = PCA(n_components=data.shape[1]) #specify number of components
pcaresult = model.fit_transform(data)
plt.plot(np.cumsum(model.explained_variance_ratio_))
plt.plot(np.repeat(1,model.explained_variance_ratio_.shape),'r--')
plt.xlabel('dims'); plt.ylabel('Cumulative Variance (%)');
plt.show()
print(model.explained_variance_ratio_)
print(np.sum(model.explained_variance_ratio_))

[2.90052934e-01 1.54217221e-01 1.39866645e-01 6.76539137e-02
 6.49586808e-02 3.77328297e-02 3.26836497e-02 2.70684145e-02
 2.34322798e-02 2.13408130e-02 2.04023716e-02 1.85849075e-02
 1.68616642e-02 1.52833017e-02 1.45935876e-02 1.34866007e-02
 1.20511650e-02 1.10991974e-02 1.01045958e-02 5.04858699e-03
 2.60581479e-03 8.70825861e-04 2.00666119e-17]
0.9999999999999998

PCA and scaling¶

In [88]:
from sklearn.datasets import load_breast_cancer

bc = load_breast_cancer()
bc_data = bc['data']
bc_outcome = bc['target']

model = PCA(n_components=2)
pcaresult = model.fit_transform(bc_data);

#scaled data
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
bc_data_scaled = scaler.fit_transform(bc_data)
model_s = PCA(n_components=2)
pcaresult_s = model_s.fit_transform(bc_data_scaled)
In [89]:
fig, (ax1,ax2) = plt.subplots(2)
ax1.scatter(pcaresult[:,0],pcaresult[:,1],c=bc_outcome,cmap=cm.rainbow)
ax1.set_xlabel('PCA1'); ax1.set_ylabel('PCA2');
ax2.scatter(pcaresult_s[:,0],pcaresult_s[:,1],c=bc_outcome,cmap=cm.rainbow)
ax2.set_xlabel('PCA1'); ax2.set_ylabel('PCA2');
plt.show()

Swiss roll¶

In [49]:
import sklearn.datasets
X,color=sklearn.datasets.make_swiss_roll(n_samples=2000)
fig = plt.figure(figsize=(10,10))
ax = plt.axes(projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=cm.Spectral);
In [41]:
%%html
<div id="howpca" style="width: 500px"></div>
<script>

    var divid = '#howpca';
	jQuery(divid).asker({
	    id: divid,
	    question: "What will the PCA projection to 2D of this data look like?",
		answers: ['Gaussian','Gradient','Spiral','Messy','Square'],
        server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
		charter: chartmaker})
    
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();


</script>
In [69]:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
fig = plt.figure(figsize=(10,10))
ax = plt.axes(projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral);
ax.set_xlabel('X0');
ax.set_ylabel('X1');
ax.set_zlabel('X2',rotation = 90);
plt.show()
In [60]:
model = PCA(n_components=2) #specify number of components
pcaresult = model.fit_transform(X_scaled)
plt.scatter(pcaresult[:,0],pcaresult[:,1],c=color,cmap=plt.cm.Spectral)
plt.xlabel('PCA1'); plt.ylabel('PCA2');
plt.show()
print(model.explained_variance_ratio_)

[0.35948427 0.33533203]
In [90]:
model = PCA(n_components=2) #specify number of components
pcaresult = model.fit_transform(X)
plt.scatter(pcaresult[:,0],pcaresult[:,1],c=color,cmap=plt.cm.Spectral)
plt.xlabel('PCA1'); plt.ylabel('PCA2');
plt.show()
print(model.explained_variance_ratio_)

[0.38553847 0.31766983]
In [67]:
plt.scatter(color,X[:,1],c=color,cmap=plt.cm.Spectral);

UMAP: Uniform Manifold Approximation & Projection¶

https://umap-learn.readthedocs.io/en/latest/index.html

Idea: Prioritize respecting local distances in embedding space.

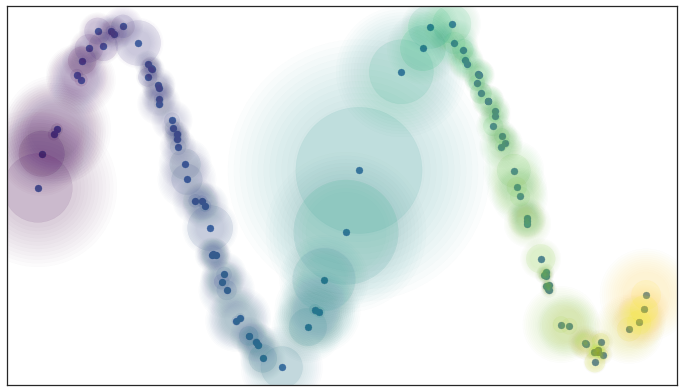
UMAP: Uniform Manifold Approximation & Projection¶

UMAP constructs a $k$-nearest neighbors graph of the data. It uses an approximate stochastic algorithm to do this quickly.

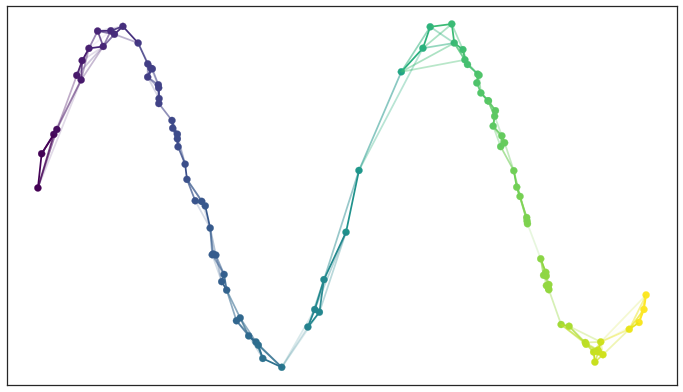
UMAP: Uniform Manifold Approximation & Projection¶

Optimizes position of data points in low dimensional space to balance attraction of locally adjacent points and repulsion of unconnected, distance points.

$$\mathrm{minimize}\sum_{e\in E} \color{blue}{ w_h(e) \log\left(\frac{w_h(e)}{w_l(e)}\right)} + \color{darkred}{(1 - w_h(e)) \log\left(\frac{1 - w_h(e)}{1 - w_l(e)}\right)}$$

$w_h(e)$ weight of edge in high dimensional space (larger weight = smaller distance)

$w_l(e)$ weight of edge in low dimensional space (larger weight = smaller distance)

This optimization is done using stochastic gradient descent starting at a deterministically constructed initial embedding.

UMAP: Uniform Manifold Approximation & Projection¶

The umap package is installed with pip3 umap-learn

In [81]:
import umap
model = umap.UMAP()
result = model.fit_transform(bc_data)
plt.scatter(result[:,0],result[:,1],s=4,c=bc_outcome,cmap=cm.Spectral);

UMAP Parameters¶

  • n_neighbors (15): Number of nearest neighbors to consider. Increase to respect global structure more.
  • min_dist (0.1): Minimum distance between points in reduced space. Decrease to have more tightly clustered points.
  • metric ("euclidean"): How distance is computed. Can provide user-supplied functions in addition to standard metrics
In [78]:
model = umap.UMAP(); result = model.fit_transform(X)
plt.scatter(result[:,0],result[:,1],s=5,c=color,cmap=plt.cm.Spectral);

n_neighbors¶

In [82]:
model = umap.UMAP(n_neighbors=3); result = model.fit_transform(X)
plt.scatter(result[:,0],result[:,1],s=5,c=color,cmap=plt.cm.Spectral);

n_neighbors¶

In [48]:
model = umap.UMAP(n_neighbors=100); result = model.fit_transform(X)
plt.scatter(result[:,0],result[:,1],s=4,c=color,cmap=plt.cm.Spectral);

min_dist¶

In [49]:
model = umap.UMAP(n_neighbors=100,min_dist=1); result = model.fit_transform(X)
plt.scatter(result[:,0],result[:,1],s=4,c=color,cmap=plt.cm.Spectral);

metric¶

In [84]:
fig,axes = plt.subplots(ncols=3,figsize=(12,6))
model = umap.UMAP(metric='euclidean')
result = model.fit_transform(X)
axes[0].scatter(result[:,0],result[:,1],s=4,c=color,cmap=plt.cm.Spectral); axes[0].set_title('euclidean')
model = umap.UMAP(metric='manhattan')
result = model.fit_transform(X)
axes[1].scatter(result[:,0],result[:,1],s=4,c=color,cmap=plt.cm.Spectral); axes[1].set_title('manhattan');
model = umap.UMAP(metric='cosine')
result = model.fit_transform(X)
axes[2].scatter(result[:,0],result[:,1],s=4,c=color,cmap=plt.cm.Spectral); axes[2].set_title('cosine');
In [85]:
fig,axes = plt.subplots(ncols=3,figsize=(12,6))
model = umap.UMAP(metric='euclidean',n_neighbors=100)
result = model.fit_transform(X)
axes[0].scatter(result[:,0],result[:,1],s=4,c=color,cmap=plt.cm.Spectral); axes[0].set_title('euclidean')
model = umap.UMAP(metric='manhattan', n_neighbors=100)
result = model.fit_transform(X)
axes[1].scatter(result[:,0],result[:,1],s=4,c=color,cmap=plt.cm.Spectral); axes[1].set_title('manhattan');
model = umap.UMAP(metric='cosine', n_neighbors=100)
result = model.fit_transform(X)
axes[2].scatter(result[:,0],result[:,1],s=4,c=color,cmap=plt.cm.Spectral); axes[2].set_title('cosine');
In [87]:
fig,axes = plt.subplots(ncols=3,figsize=(12,6))
model = umap.UMAP(metric='euclidean',n_neighbors=100,min_dist=1)
result = model.fit_transform(X)
axes[0].scatter(result[:,0],result[:,1],s=4,c=color,cmap=plt.cm.Spectral); axes[0].set_title('euclidean')
model = umap.UMAP(metric='manhattan', n_neighbors=100,min_dist=1)
result = model.fit_transform(X)
axes[1].scatter(result[:,0],result[:,1],s=4,c=color,cmap=plt.cm.Spectral); axes[1].set_title('manhattan');
model = umap.UMAP(metric='cosine', n_neighbors=100,min_dist=1)
result = model.fit_transform(X)
axes[2].scatter(result[:,0],result[:,1],s=4,c=color,cmap=plt.cm.Spectral); axes[2].set_title('cosine');

UMAP vs. t-SNE¶

t-SNE (t-distributed stochastic neighbor embedding) is an older method that also uses a notion of preserving local distances

  • doesn't use nearest neighbor graph (slower)
  • different cost function for optimizing embedding
  • more sensitive to parameters
  • default to stochastic initialization of optimization

Project¶

Download the below heavily downsampled RNASeq data and visualize it in 2D both with PCA and UMAP.

Color the points by the labels.

In [51]:
!wget  http://mscbio2025.net/files/mouse_data/X.csv.gz
!wget  http://mscbio2025.net/files/mouse_data/obs.csv

--2023-10-30 20:50:53--  http://mscbio2025.net/files/mouse_data/X.csv.gz
Resolving mscbio2025.net (mscbio2025.net)... 185.199.108.153, 185.199.111.153, 185.199.109.153, ...
Connecting to mscbio2025.net (mscbio2025.net)|185.199.108.153|:80... connected.
HTTP request sent, awaiting response... 301 Moved Permanently
Location: https://mscbio2025.net/files/mouse_data/X.csv.gz [following]
--2023-10-30 20:50:53--  https://mscbio2025.net/files/mouse_data/X.csv.gz
Connecting to mscbio2025.net (mscbio2025.net)|185.199.108.153|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 5447648 (5.2M) [application/gzip]
Saving to: ‘X.csv.gz.1’

X.csv.gz.1          100%[===================>]   5.19M  --.-KB/s    in 0.05s   

2023-10-30 20:50:53 (103 MB/s) - ‘X.csv.gz.1’ saved [5447648/5447648]

--2023-10-30 20:50:53--  http://mscbio2025.net/files/mouse_data/obs.csv
Resolving mscbio2025.net (mscbio2025.net)... 185.199.108.153, 185.199.109.153, 185.199.110.153, ...
Connecting to mscbio2025.net (mscbio2025.net)|185.199.108.153|:80... connected.
HTTP request sent, awaiting response... 301 Moved Permanently
Location: https://mscbio2025.net/files/mouse_data/obs.csv [following]
--2023-10-30 20:50:53--  https://mscbio2025.net/files/mouse_data/obs.csv
Connecting to mscbio2025.net (mscbio2025.net)|185.199.108.153|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 101150 (99K) [text/csv]
Saving to: ‘obs.csv.1’

obs.csv.1           100%[===================>]  98.78K  --.-KB/s    in 0.008s  

2023-10-30 20:50:53 (12.8 MB/s) - ‘obs.csv.1’ saved [101150/101150]
In [52]:
data = np.genfromtxt('X.csv.gz',delimiter=',')
labels = np.genfromtxt('obs.csv',delimiter=',',dtype=str,skip_header=1)[:,1]
In [53]:
#convert labels (strings) to numbers so they can be used as colors in matplotlib
from sklearn import preprocessing
colors = preprocessing.LabelEncoder().fit_transform(labels)
In [54]:
data.shape
Out[54]:
(1196, 4286)
In [55]:
labels.shape
Out[55]:
(1196,)
In [ ]:
#can use umap's plotting function and provide labels as strings
import umap.plot
In [ ]:
pca = PCA(n_components=2)
pcaD = pca.fit_transform(data)
plt.scatter(pcaD[:,0],pcaD[:,1],s=4,c=colors)
plt.xlabel('PCA1'); plt.ylabel('PCA2');
In [ ]:
model = umap.UMAP(n_neighbors=100)
uD = model.fit(data)
umap.plot.points(uD, labels=labels)