%%html
<script src="https://bits.csb.pitt.edu/preamble.js"></script>
OMET Teaching Survey¶
Please fill out.
Perceptron¶
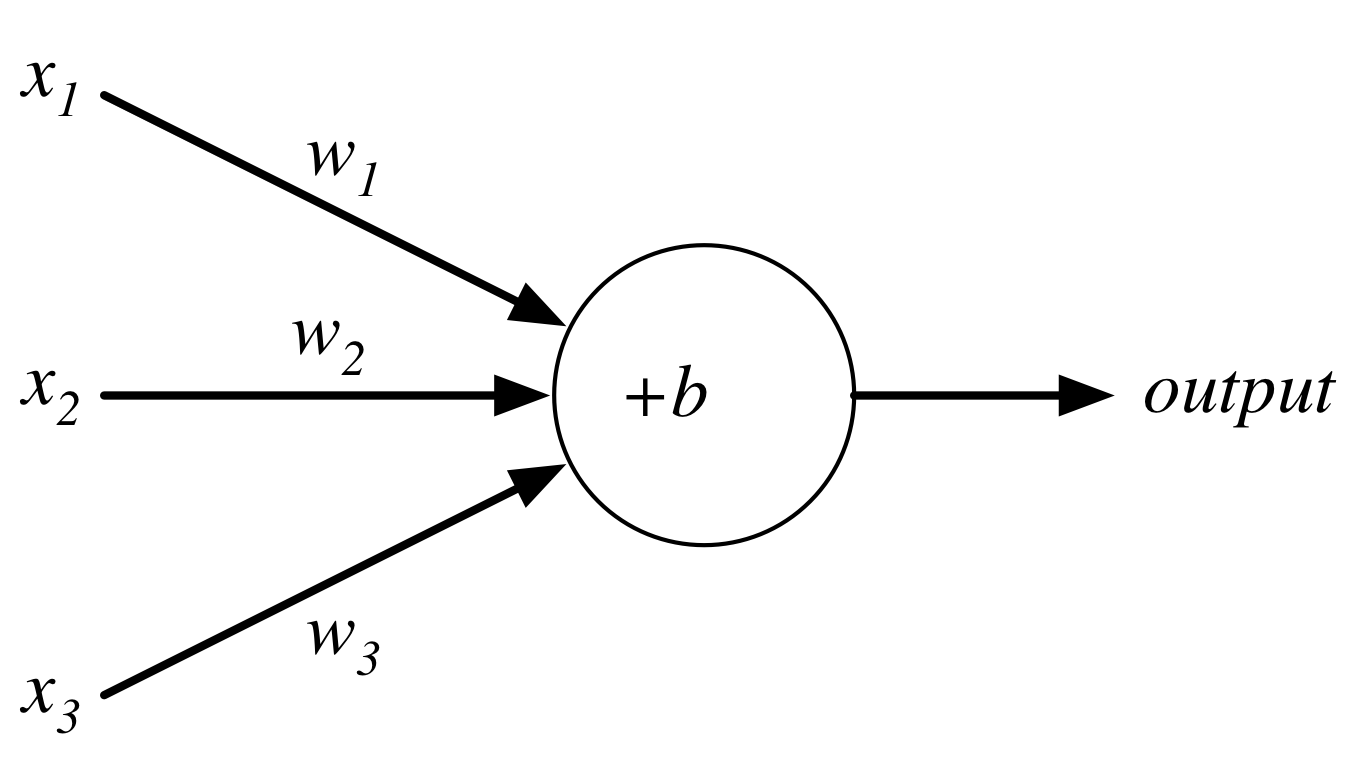
$$output = \begin{cases} 0 \text{ if } w\cdot x + b \le 0 \\ 1 \text{ if } w\cdot x + b > 0 \end{cases}$$
Perceptron¶
Consider the following perceptron:
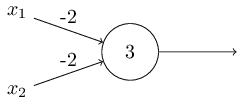
If $x$ takes on only binary values, what are the possible outputs?
%%html
<div id="inand" style="width: 500px"></div>
<script>
var divid = '#inand';
jQuery(divid).asker({
id: divid,
question: "What are the corresponding outputs for x = [0,0],[0,1],[1,0], and [1,1]?",
answers: ["0,0,0,0","0,1,1,0","0,0,0,1","0,1,1,1","1,1,1,0"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
Neurons¶
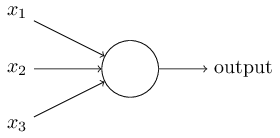
Instead of a binary output, we set the output to the result of an activation function $\sigma$
$$output = \sigma(w\cdot x + b)$$
Activation Functions: Step (Perceptron)¶
plt.plot(x, x > 0,linewidth=1,clip_on=False);
plt.hlines(xmin=-10,xmax=0,y=0,linewidth=3,color='b')
plt.hlines(xmin=0,xmax=10,y=1,linewidth=3,color='b');
Activation Functions: Sigmoid (Logistic)¶
plt.plot(x, 1/(1+np.exp(-x)),linewidth=4,clip_on=False);
plt.plot(x, 1/(1+np.exp(-2*x)),linewidth=2,clip_on=False);
plt.plot(x, 1/(1+np.exp(-.5*x)),linewidth=2,clip_on=False);
Activation Functions: tanh¶
plt.plot([-10,10],[0,0],'k--')
plt.plot(x, np.tanh(x),linewidth=4,clip_on=False);
Activation Functions: ReLU¶
Rectified Linear Unit: $\sigma(z) = \max(0,z)$
plt.plot(x,x*(x > 0),clip_on=False,linewidth=4);
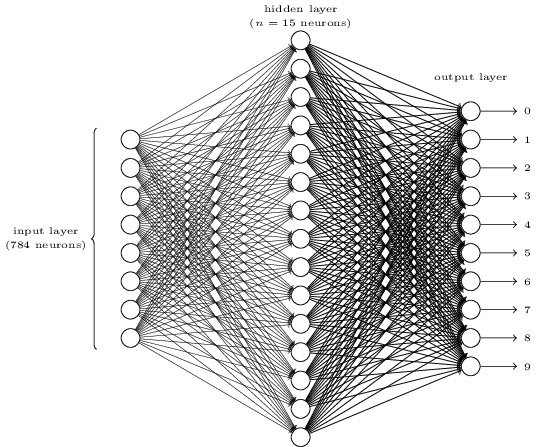
Networks¶
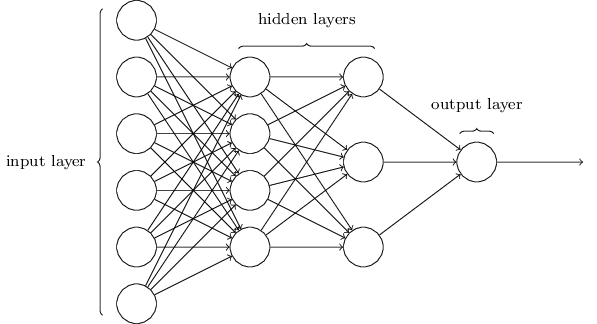
Terminology alert: networks of neurons are sometimes called multilayer perceptrons, despite not using the step function.
%%html
<div id="ibpcnt" style="width: 500px"></div>
<script>
var divid = '#ibpcnt';
jQuery(divid).asker({
id: divid,
question: "A network has 10 input nodes, two hidden layers each with 10 neurons, and 10 output neurons. How many parameters does training have to estimate?",
answers: ["30","100","300","330","600"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
Networks¶
 The number of input neurons corresponds to the number of features.
The number of input neurons corresponds to the number of features.
The number of output neurons corresponds to the number of label classes. For binary classification, it is common to have two output nodes.
Layers are typically fully connected.
Neural Networks¶
The universal approximation theorem says that, if some reasonable assumptions are made, a feedforward neural network with a finite number of nodes can approximate any continuous function to within a given error $\epsilon$ over a bounded input domain.
The theorem says nothing about the design (number of nodes/layers) of such a network.
The theorem says nothing about the learnability of the weights of such a network.
These are open theoretical questions.
Given a network design, how are we going to learn weights for the neurons?
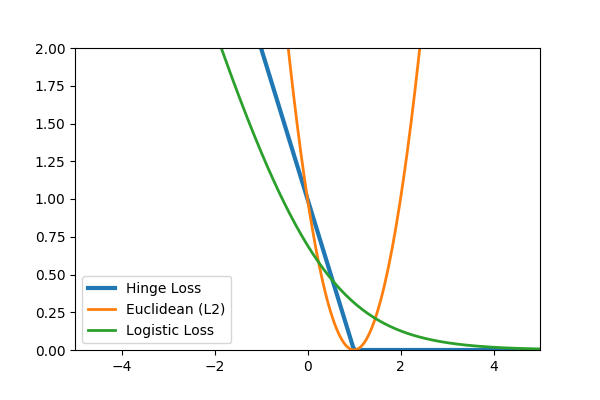
Stochastic Gradient Descent¶
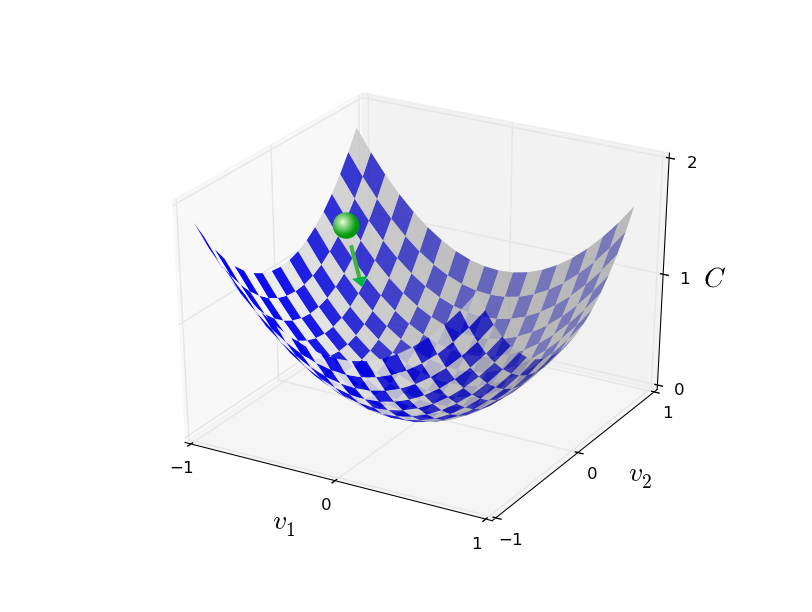
Randomly select $m$ training examples $X_j$ and compute the gradient of the loss function ($L$). Update weights and biases with a given learning rate $\eta$. $$ w_k' = w_k-\frac{\eta}{m}\sum_j^m \frac{\partial L_{X_j}}{\partial w_k}$$ $$b_l' = b_l-\frac{\eta}{m} \sum_j^m \frac{\partial L_{X_j}}{\partial b_l} $$
Common loss functions: logistic, hinge, cross entropy, euclidean
Backpropagation¶
Backpropagation is an efficient algorithm for computing the partial derivatives needed by the gradient descent update rule. For a training example $x$ and loss function $L$ in a network with $N$ layers:
Feedforward. For each layer $l$ compute $$a^{l} = \sigma(z^{l})$$ where $z$ is the weighted input and $a$ is the activation induced by $x$ (these are vectors representing all nodes of layer $l$).
Compute output error $$\delta^{N} = \nabla_a L \odot \sigma'(z^N)$$ where $ \nabla_a L_j = \partial L / \partial a^N_j$, the gradient of the loss with respect to the output activations. $\odot$ is the elementwise product.
Backpropagate the error $$\delta^{l} = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^{l})$$
Calculate gradients $$\frac{\partial L}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j \text{ and } \frac{\partial L}{\partial b^l_j} = \delta^l_j$$
Backpropagation as the Chain Rule¶
$$\frac{\partial L}{\partial a^l} \cdot \frac{\partial a^l}{\partial z^l} \cdot \frac{\partial z^l}{\partial a^{l-1}} \cdot \frac{\partial a^{l-1}}{\partial z^{l-1}} \cdot \frac{\partial z^{l-1}}{\partial a^{l-2}} \cdots \frac{\partial a^{1}}{\partial z^{l}} \cdot \frac{\partial z^{l}}{\partial x} $$
Deep Learning¶
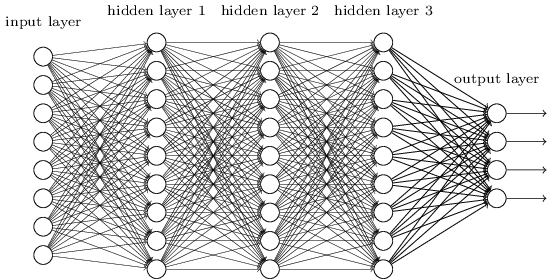
A deep network is not more powerful (recall can approximate any function with a single layer), but may be more concise - can approximate some functions with many fewer nodes.
Convolution Filters¶
A filter applies a convolution kernel to an image.
The kernel is represented by an $n$x$n$ matrix where the target pixel is in the center.
The output of the filter is the sum of the products of the matrix elements with the corresponding pixels.
Examples from Wikipedia):
 |

|

|
| Identity | Blur | Edge Detection |
Feature Maps¶
We can think of a kernel as identifying a feature in an image and the resulting image as a feature map that has high values (white) where the feature is present and low values (black) elsewhere.
Feature maps retain the spatial relationship between features present in the original image.
Convolutional Layers¶
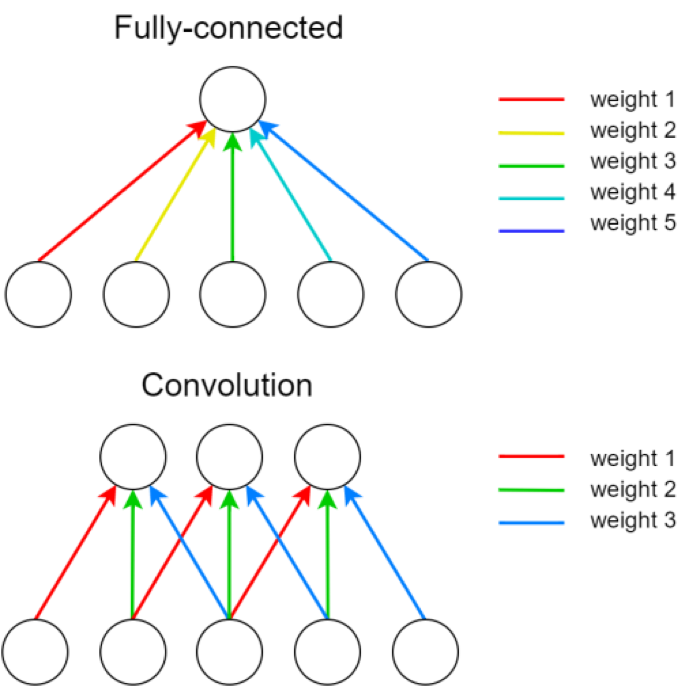 A single kernel is applied across the input. For each output feature map there is a single set of weights.
A single kernel is applied across the input. For each output feature map there is a single set of weights.
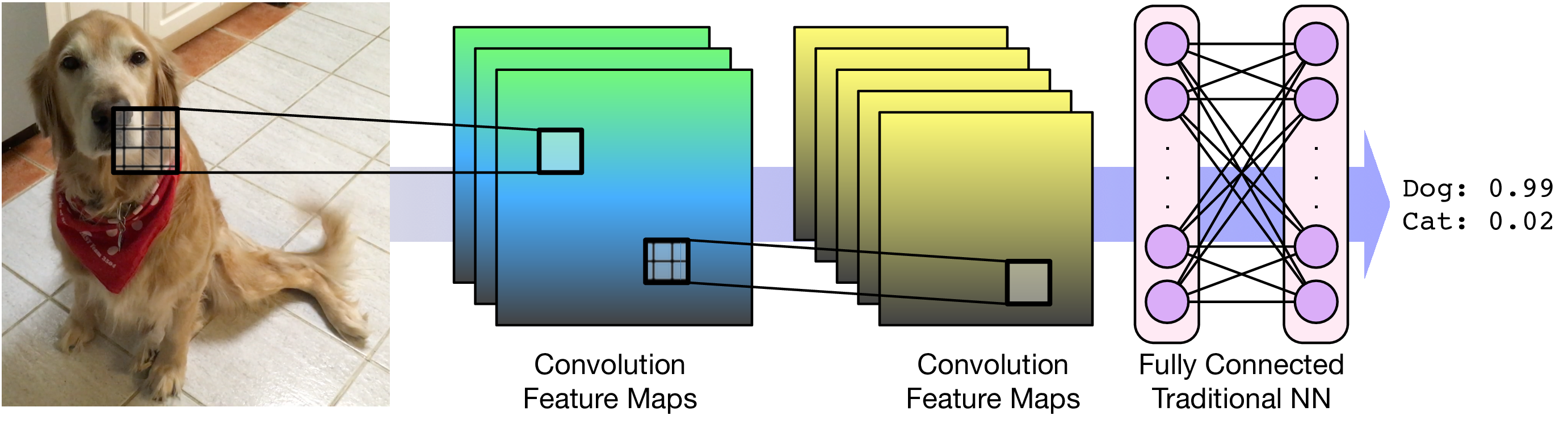
Convolutional Layers¶
For images, each pixel is an input feature. Each hidden layer is a set of feature maps.

Pooling¶
Pooling layers apply a fixed convolution (usually the non-linear MAX kernel). The kernel is usually applied with a stride to reduce the size of the layer.
- faster to train
- fewer parameters to fit
- less sensitive to small changes (MAX)

Consider an input image with 100 pixels. In a classic neural network, we hook these pixels up to a hidden layer with 10 nodes. In a CNN, we hook these pixels up to a convolutional layer with a 3x3 kernel and 10 output feature maps.
%%html
<div id="iweightcnt" style="width: 500px"></div>
<script>
var divid = '#iweightcnt';
jQuery(divid).asker({
id: divid,
question: "Which network has more parameters to learn?",
answers: ["Classic","CNN"],
server: "https://bits.csb.pitt.edu/asker.js/example/asker.cgi",
charter: chartmaker})
$(".jp-InputArea .o:contains(html)").closest('.jp-InputArea').hide();
</script>
PyTorch Tensors¶
Tensor is very similar to numpy.array in functionality.
- Is allocated to a device (CPU vs GPU)
- Potentially maintains autograd information
import torch # note package is not called pytorch
T = torch.rand(3,4)
T
tensor([[0.6449, 0.8679, 0.7000, 0.7213],
[0.7735, 0.5921, 0.2053, 0.5418],
[0.5145, 0.2320, 0.5560, 0.0838]])
T.shape,T.dtype,T.device,T.requires_grad
(torch.Size([3, 4]), torch.float32, device(type='cpu'), False)
Modules vs Functional¶
Modules are objects that can be initialized with default parameters and store any learnable parameters. Learnable parameters can be easily extracted from the module (and any member modules). Modules are called as functions on their inputs.
Functional APIs maintain no state. All parameters are passed when the function is called.
import torch.nn as nn
import torch.nn.functional as F
A network is a module¶
To define a network we create a module with submodules for operations with learnable parameters. Generally use functional API for operations without learnable parameters.
class MyNet(nn.Module):
def __init__(self): #initialize submodules here - this defines our network architecture
super(MyNet, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3, stride=1, padding=1)
self.conv2 = nn.Conv2d(in_channels=32, out_channels=64, kernel_size=3, stride=1)
self.fc1 = nn.Linear(2304, 10) #mystery X
def forward(self, x): # this actually applies the operations
x = self.conv1(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2, stride=2) # POOL
x = self.conv2(x)
x = F.relu(x)
x = F.max_pool2d(x, kernel_size=2, stride=2) # POOL
x = torch.flatten(x, 1)
x = self.fc1(x)
return x
MNIST¶
from torchvision import datasets
train_data = datasets.MNIST(root='../data', train=True,download=True)
test_data = datasets.MNIST(root='../data', train=False)
train_data[0]
(<PIL.Image.Image image mode=L size=28x28 at 0x7F25E2ED6FB0>, 5)
train_data[0][0]
Inputs need to be tensors...
from torchvision import transforms
train_data = datasets.MNIST(root='../data', train=True,transform=transforms.ToTensor())
test_data = datasets.MNIST(root='../data', train=False,transform=transforms.ToTensor())
train_data[0][0]
tensor([[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0118, 0.0706, 0.0706, 0.0706,
0.4941, 0.5333, 0.6863, 0.1020, 0.6510, 1.0000, 0.9686, 0.4980,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.1176, 0.1412, 0.3686, 0.6039, 0.6667, 0.9922, 0.9922, 0.9922,
0.9922, 0.9922, 0.8824, 0.6745, 0.9922, 0.9490, 0.7647, 0.2510,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1922,
0.9333, 0.9922, 0.9922, 0.9922, 0.9922, 0.9922, 0.9922, 0.9922,
0.9922, 0.9843, 0.3647, 0.3216, 0.3216, 0.2196, 0.1529, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0706,
0.8588, 0.9922, 0.9922, 0.9922, 0.9922, 0.9922, 0.7765, 0.7137,
0.9686, 0.9451, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.3137, 0.6118, 0.4196, 0.9922, 0.9922, 0.8039, 0.0431, 0.0000,
0.1686, 0.6039, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0549, 0.0039, 0.6039, 0.9922, 0.3529, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.5451, 0.9922, 0.7451, 0.0078, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0431, 0.7451, 0.9922, 0.2745, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.1373, 0.9451, 0.8824, 0.6275,
0.4235, 0.0039, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.3176, 0.9412, 0.9922,
0.9922, 0.4667, 0.0980, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1765, 0.7294,
0.9922, 0.9922, 0.5882, 0.1059, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0627,
0.3647, 0.9882, 0.9922, 0.7333, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.9765, 0.9922, 0.9765, 0.2510, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1804, 0.5098,
0.7176, 0.9922, 0.9922, 0.8118, 0.0078, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.1529, 0.5804, 0.8980, 0.9922,
0.9922, 0.9922, 0.9804, 0.7137, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0941, 0.4471, 0.8667, 0.9922, 0.9922, 0.9922,
0.9922, 0.7882, 0.3059, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0902, 0.2588, 0.8353, 0.9922, 0.9922, 0.9922, 0.9922, 0.7765,
0.3176, 0.0078, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0706, 0.6706,
0.8588, 0.9922, 0.9922, 0.9922, 0.9922, 0.7647, 0.3137, 0.0353,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.2157, 0.6745, 0.8863, 0.9922,
0.9922, 0.9922, 0.9922, 0.9569, 0.5216, 0.0431, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.5333, 0.9922, 0.9922, 0.9922,
0.8314, 0.5294, 0.5176, 0.0627, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000]]])
plt.imshow(train_data[0][0][0])
<matplotlib.image.AxesImage at 0x7f25e3198250>
Training MNIST¶
#process 10 randomly sampled images at a time
train_loader = torch.utils.data.DataLoader(train_data,batch_size=10,shuffle=True)
test_loader = torch.utils.data.DataLoader(test_data,batch_size=10,shuffle=False)
#instantiate our neural network and put it on the GPU
model = MyNet().to('cuda')
batch = next(iter(train_loader))
batch
[tensor([[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]],
[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]],
[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]],
...,
[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]],
[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]],
[[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]]]),
tensor([3, 4, 2, 2, 0, 0, 4, 8, 4, 7])]
output = model(batch[0].to('cuda')) # model is on GPU, so must put input there too
output
tensor([[-0.0618, 0.0725, 0.0696, 0.0907, 0.0204, -0.1858, 0.0752, 0.0432,
-0.1025, -0.0215],
[-0.0696, 0.0885, -0.0112, 0.1133, 0.0270, -0.1915, 0.1485, -0.0218,
-0.1089, 0.0137],
[-0.0315, 0.0997, 0.0130, 0.0563, 0.0575, -0.1342, 0.1309, 0.0970,
-0.0519, 0.0064],
[-0.0242, 0.0943, 0.0179, 0.0685, 0.0844, -0.2072, 0.0581, 0.1100,
-0.1413, 0.0031],
[-0.0648, 0.0661, 0.0950, 0.0312, 0.0466, -0.1491, 0.0859, 0.0665,
-0.0603, 0.0305],
[-0.0315, 0.0449, 0.0610, 0.1021, 0.0320, -0.1344, 0.1114, 0.0320,
-0.0648, 0.0369],
[-0.0270, 0.0672, 0.0473, 0.0491, 0.0293, -0.1694, 0.0731, 0.0291,
-0.1106, 0.0358],
[-0.0456, 0.0428, 0.0516, 0.0689, 0.0399, -0.2126, 0.0604, 0.0615,
-0.0844, -0.0294],
[-0.0477, 0.0740, 0.0625, 0.0808, 0.0134, -0.1671, 0.1014, 0.0406,
-0.1062, 0.0309],
[-0.0168, 0.0673, 0.0582, 0.0483, 0.0313, -0.1919, 0.0552, 0.0547,
-0.0937, 0.0116]], device='cuda:0', grad_fn=<AddmmBackward0>)
Training MNIST¶
Our network takes an image (as a tensor) and outputs class probabilities.
- Need a loss
- Need an optimizer (e.g. SGD, ADAM)
backwarddoes not update parameters
loss = F.cross_entropy(output,batch[1].to('cuda')) #combines log softmax and
loss
tensor(2.3067, device='cuda:0', grad_fn=<NllLossBackward0>)
$$L(x,class) = - \log\left(\frac{e^{x_{\mathrm{class}}}}{\sum_j e^{x_j}}\right)$$
loss.backward() # sets grad, but does not change parameters of model
Training MNIST¶
Epoch - One pass through the training data.
%%time
optimizer = torch.optim.Adam(model.parameters(), lr=0.00001) # need to tell optimizer what it is optimizing
losses = []
for epoch in range(10):
for i, (img,label) in enumerate(train_loader):
optimizer.zero_grad() # IMPORTANT!
img, label = img.to('cuda'), label.to('cuda')
output = model(img)
loss = F.cross_entropy(output, label)
loss.backward()
optimizer.step()
losses.append(loss.item())
CPU times: user 3min 44s, sys: 1.69 s, total: 3min 46s Wall time: 3min 50s
plt.plot(losses)
[<matplotlib.lines.Line2D at 0x7f25e042d120>]
This is the batch loss.
Testing MNIST¶
correct = 0
with torch.no_grad(): #no need for gradients - won't be calling backward to clear them
for img, label in test_loader:
img, label = img.to('cuda'), label.to('cuda')
output = F.softmax(model(img),dim=1)
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(label.view_as(pred)).sum().item()
print("Accuracy",correct/len(test_loader.dataset))
Accuracy 0.9684
Some Failures¶
*Not from this particular network

Generative vs. Discriminative¶
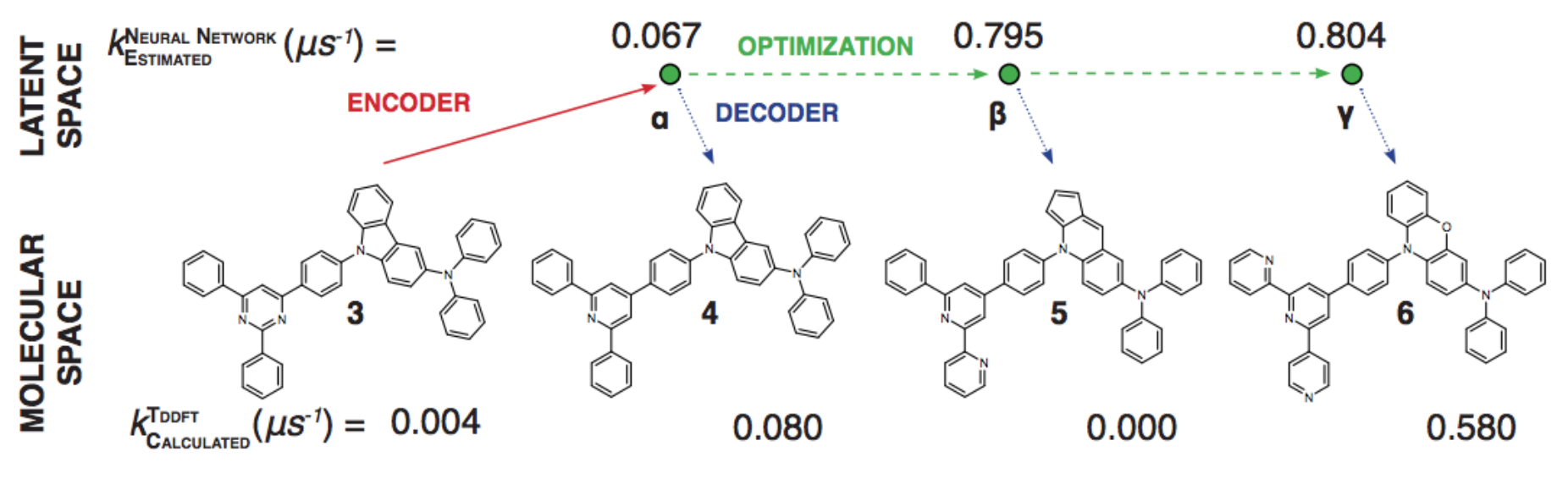
A generative model produces as output the input of a discriminative model: $P(X|Y=y)$ or $P(X,Y)$
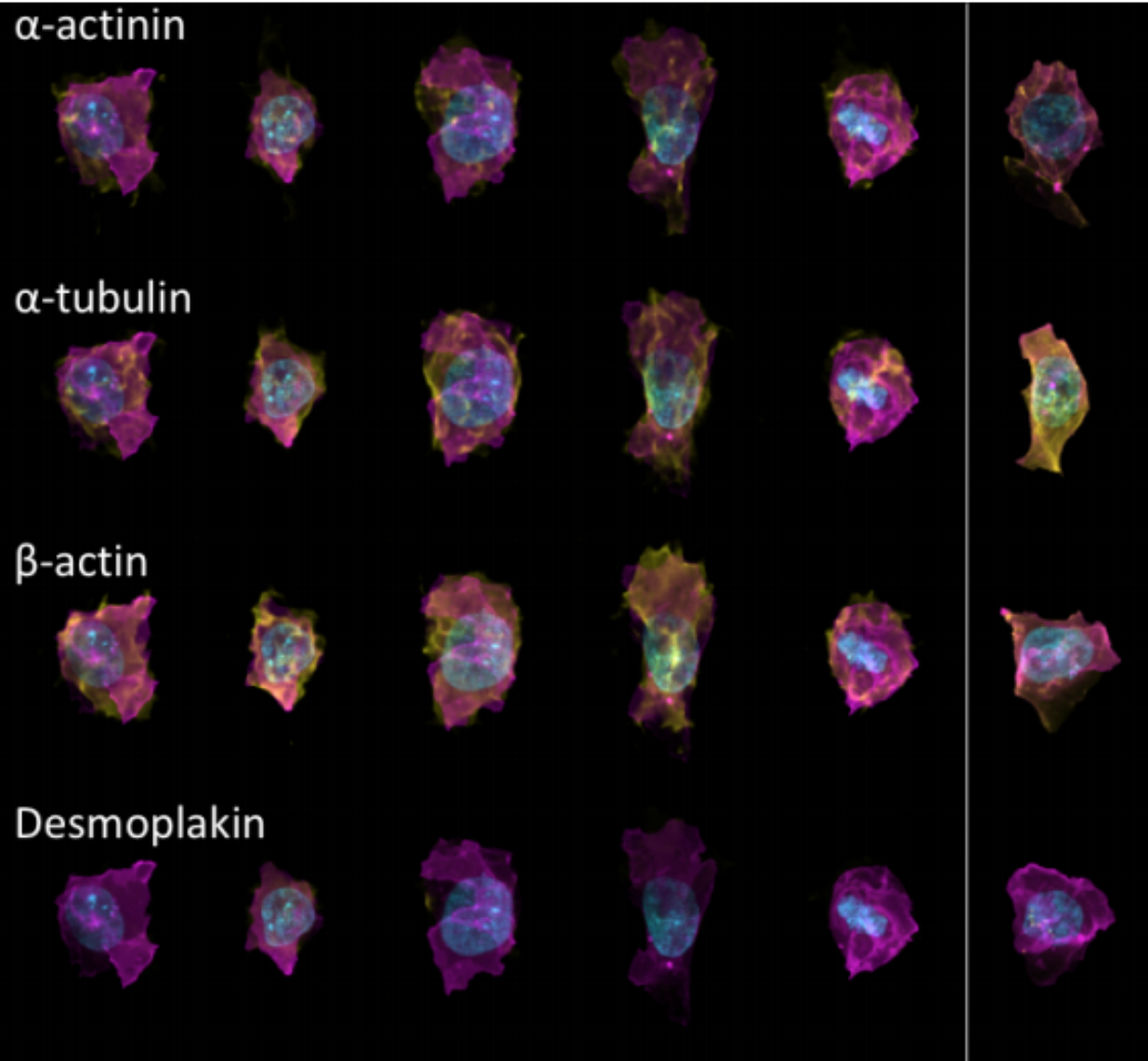
Generative Models of the Cell¶
https://arxiv.org/pdf/1705.00092.pdf
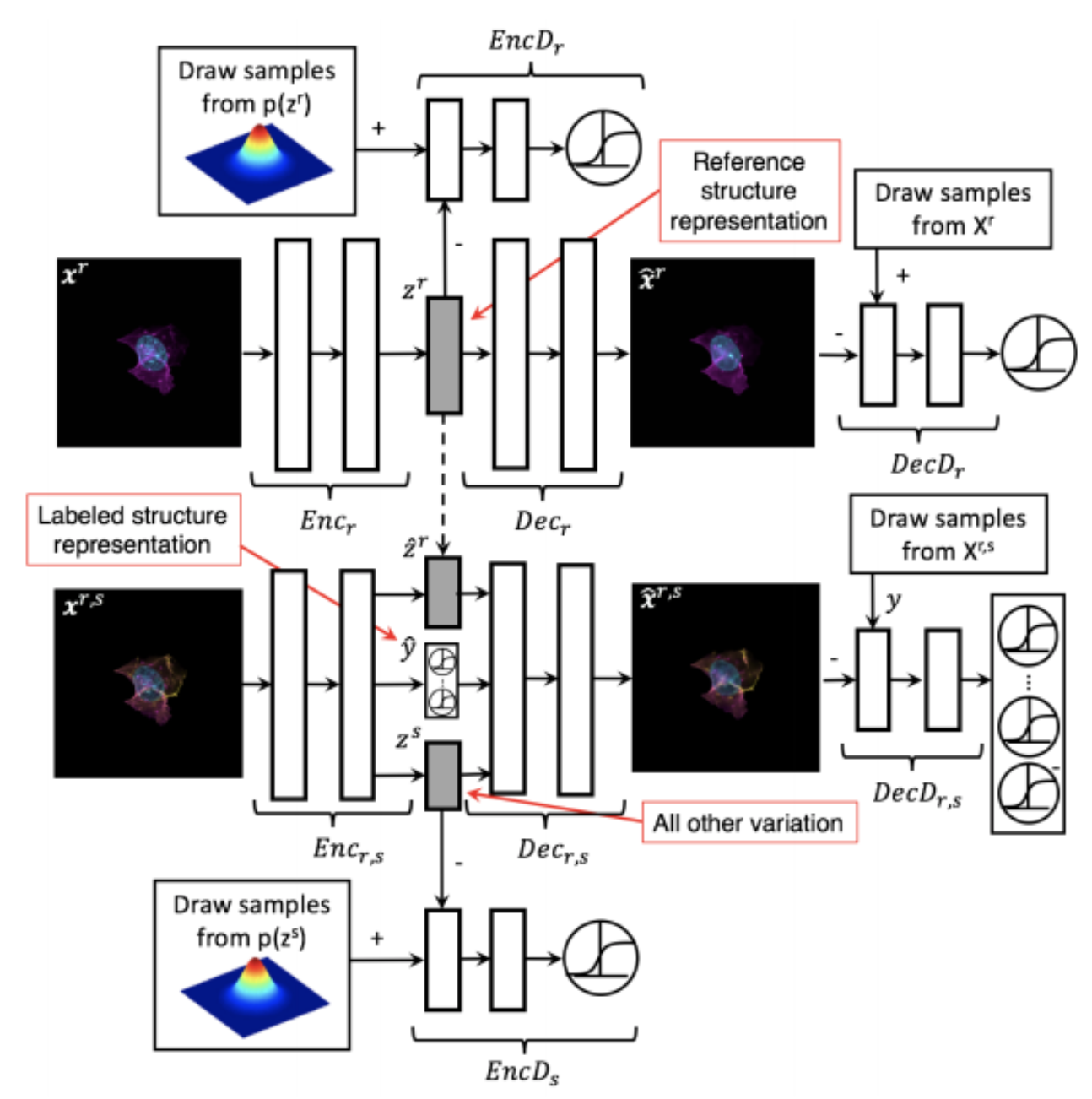
|
|
https://drive.google.com/file/d/0B2tsfjLgpFVhMnhwUVVuQnJxZTg/view
Generative Adversarial Networks¶
https://arxiv.org/abs/1406.2661
 https://youtu.be/G06dEcZ-QTg
https://youtu.be/G06dEcZ-QTg
Deep learning is not profound learning.¶
But it is quite powerful and flexible.
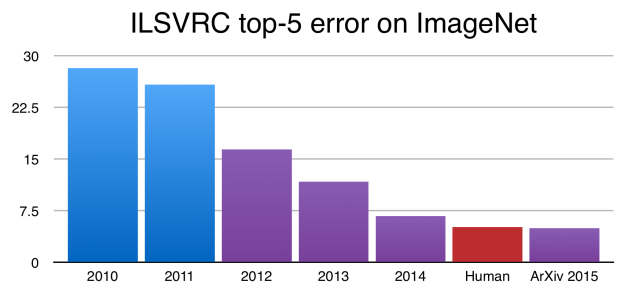
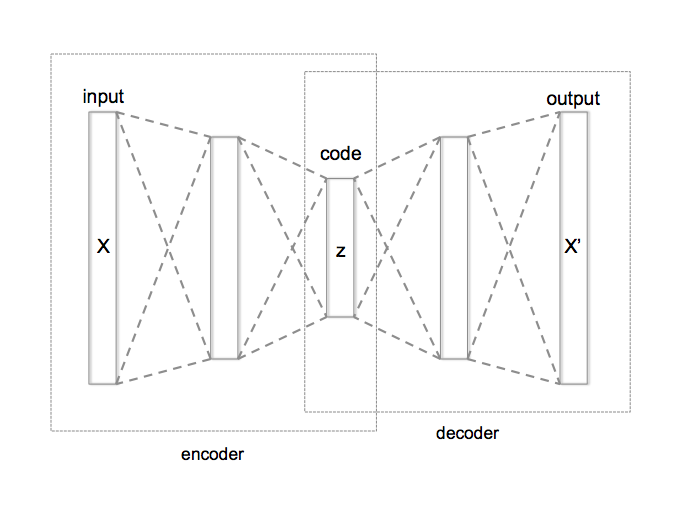

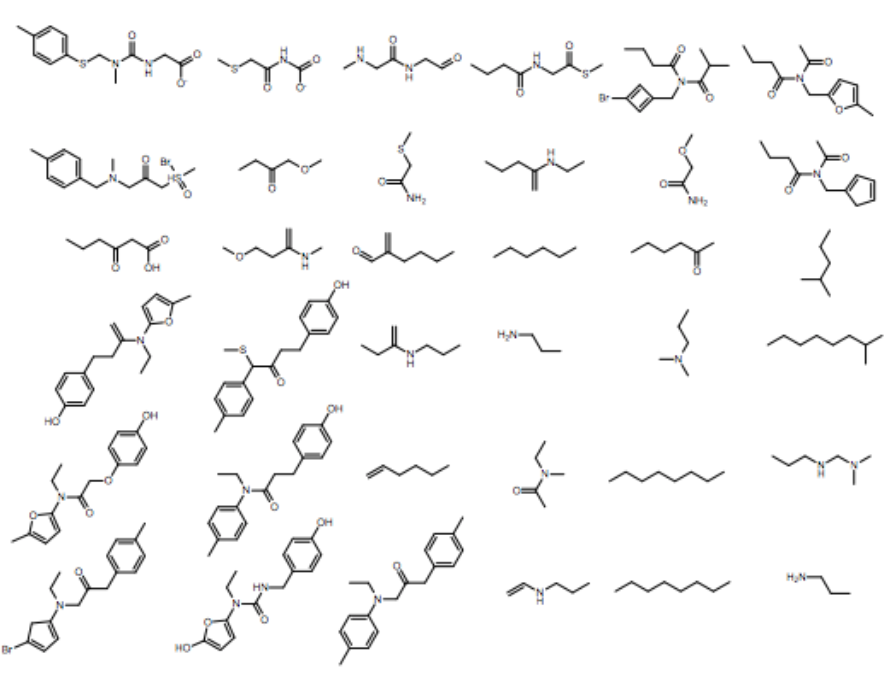
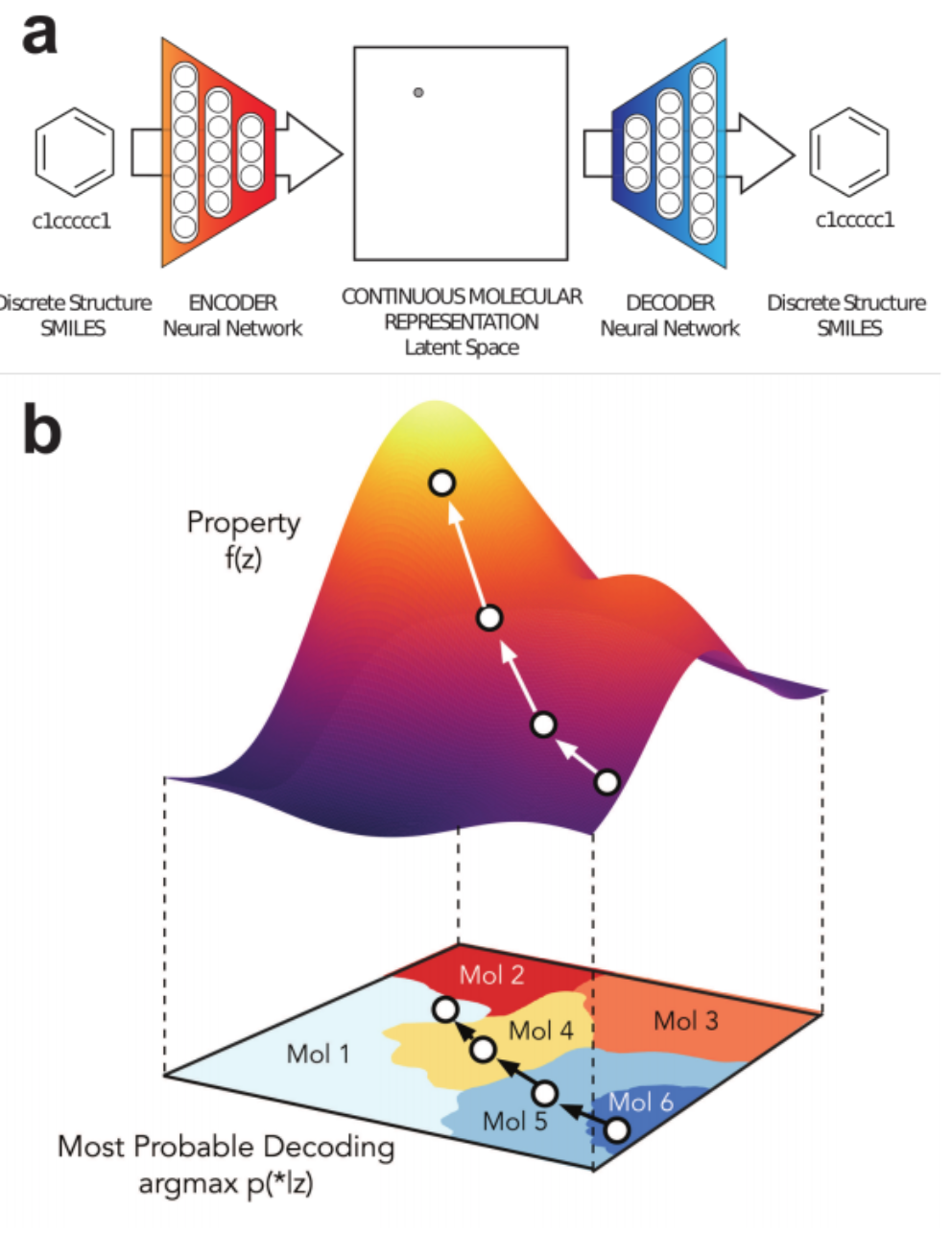 1% - 70% of output valid SMILES
1% - 70% of output valid SMILES